Усечённая четырёх-шестиугольная мозаика

Усечённая четырёх-шестиугольная мозаика — это a полурегулярная мозаика на гиперболической плоскости. В этой мозаике в каждой вершине сходятся один квадрат, один восьмиугольник, и один двенадцатиугольник. Мозаика имеет символ Шлефли tr{6,4}.

Усечённая четырёх-шестиугольная мозаика
Тип	Гиперболическая однородная мозаика
Конфигурация вершины	4.8.12
Символ Шлефли	t{6,4} или ${\displaystyle t{\begin{Bmatrix}6\\4\end{Bmatrix}}}$
Символ Витхоффа	2 6 | 4
Симметрии	[6,4], (*642)
Диаграммы Коксетера — Дынкина	или
Двойственные соты	кис-ромбическая мозаика порядка 4-6
Свойства	Изогональная

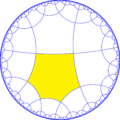
Двойственная мозаика

Двойственная мозаика называется кис-ромбической мозаикой порядка 4-6, состоящей из полного разбиения шестиугольной мозаики порядка 4[англ.][1]. На рисунке треугольники показаны в чередующихся цветах. Эта мозаика представляет фундаментальную треугольную область с симметрией [6,4] (*642).

Связанные многогранники и мозаики

*n42 симметрии общеусечённых мозаик: 4.8.2n

Симметрия *n42 [n,4]	Сферическая		Евклидова	Компактная гиперболическая				Паракомп.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]…	*∞42 [∞,4]
Общеусечённая фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Общеусечённые двойственные	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 мутации симметрий всеусечённых мозаик: 4.2n.2n
Симметрия *nn2 [n,n]	Сферическая		Евклидова	Компактная гиперболическая				Паракомпактная
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Рисунок
Конф.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Двойственная фигура
Конф.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

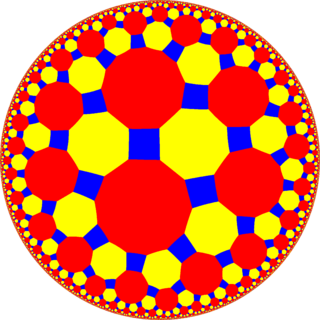
Согласно построению Витхоффа существует 14 гиперболических одородных мозаик, базирующихся на правильной шестиугольной мозаике порядка 4.

Если рисовать мозаики с выделенными красным цветом исходными фигурами, жёлтым цветом исходными вершинами и синим цветом исходными рёбрами, получим 7 рисунков с полной [6,4] симметрией и 7 с подсимметрией.

Однородные четырёхшестиугольные мозаики
Симметрия: [6,4], (*642) ( [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (и [(∞,3,∞,3)] (*3232) подсимметрия)
= = =	=	= = =	=	= = =	=
{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Однородные двойственные duals
V64	V4.12.12	V(4.6)2	V6.8.8	V46	V4.4.4.6	V4.8.12
Альтернирования
[1+,6,4] (*443)	[6+,4] (6*2)	[6,1+,4] (*3222)	[6,4+] (4*3)	[6,4,1+] (*662)	[(6,4,2+)] (2*32)	[6,4]+ (642)
=	=	=	=	=	=
h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Симметрия

Усечённая четырёх-шестиугольная мозаика с зелёными, красными и синими линиями отражения:

Диаграммы симметрии для подгрупп [6,4] с малым индексом, показанными в шестиугольных ячейках {6,6} мозаики^[англ.] с выделенной жёлтым цветом фундаментальной областью.

Мозаика, двойственная рассматриваемой, представляет фундаментальную область (*642) с орбифолдной^[англ.] симметрией. Из симметрии [6,4] следует, что имеется 15 подгрупп малого индекса, получаемых удалением зеркального отражения и операцией альтернации^[англ.]. Отражения могут быть удалены, если все порядки ветвей чётны. Удаление двух отражений оставляет точку вращения половинного порядка в месте пересечения зеркал. В этих рисунках оси отражений (зеркала) показаны красным, зелёным и синим цветом, а треугольники с чередующейся окраской показывают положение точек вращения. Подгруппа [6⁺,4⁺], (32×) имеет тонкие линии, представляющие скользящие отражения. Группа [1⁺,6,1⁺,4,1⁺] (3232) с индексом 8 является коммутантом группы [6,4].

Бо́льшая подгруппа, построенная как [6,4*] путём удаления точек вращения [6,4⁺], (3*22) с индексом 6 становится (*3333^[англ.]), а группа, построенная как [6*,4] путём удаления точек вращения [6⁺,4], (2*33) с индексом 12 становится (*222222^[англ.]). Наконец, их прямые подгруппы^[2] [6,4*]⁺, [6*,4]⁺, с индексами 12 и 24 соответственно, можно задать в орбифолдной нотации как (3333) и (222222).

Подгруппы [6,4] с малым индексом
Индекс	1	2			4
Диаграмма
Коксетер[англ.]	[6,4] = =	[1+,6,4] =	[6,4,1+] = =	[6,1+,4] =	[1+,6,4,1+] =	[6+,4+]
Генераторы	{0,1,2}	{1,010,2}	{0,1,212}	{0,101,2,121}	{1,010,212,20102}	{012,021}
Орбифолд[англ.]	*443[англ.]	*662[англ.]	*3222[англ.]	*3232[англ.]	32×
Полупрямые подгруппы
Диаграмма
Коксетер		[6,4+]	[6+,4]	[(6,4,2+)]	[6,1+,4,1+] = = = =	[1+,6,1+,4] = = = =
Генераторы		{0,12}	{01,2}	{1,02}	{0,101,1212}	{0101,2,121}
Орбифолд		4*3	6*2	2*32	2*33	3*22
Прямые подгруппы
Индекс	2	4			8
Диаграмма
Коксетер	[6,4]+ =	[6,4+]+ =	[6+,4]+ =	[(6,4,2+)]+ =	[6+,4+]+ = [1+,6,1+,4,1+] = = =
Генераторы	{01,12}	{(01)2,12}	{01,(12)2}	{02,(01)2,(12)2}	{(01)2,(12)2,2(01)22}
Орбифолд	642	443	662	3222	3232
Радикальные подгруппы
Индекс		8	12	16	24
Диаграмма
Коксетер		[6,4*] =	[6*,4]	[6,4*]+ =	[6*,4]+
Орбифолд		*3333[англ.]	*222222[англ.]	3333	222222

См. также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на плоскости^[англ.]