Усечённая четырёх-восьмиугольная мозаика

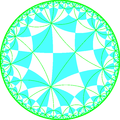
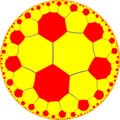
Усечённая четырёх-восьмиугольная мозаика — это a полурегулярная мозаика на гиперболической плоскости. Мозаике имеет один квадрат, один восьмиугольник и один шестнадцатиугольник в каждой вершине. Мозаика имеет символ Шлефли tr{8,4}.

Усечённая четырёх-восьмиугольная мозаика
Тип	Гиперболическая однородная мозаика
Конфигурация вершины	4.8.16
Символ Шлефли	t{8,4} или ${\displaystyle t{\begin{Bmatrix}8\\4\end{Bmatrix}}}$
Символ Витхоффа	2 8 4 |
Симметрии	[8,4], (*842)
Диаграммы Коксетера — Дынкина	или
Двойственные соты	кис-ромбическая мозаика порядка 4-8
Свойства	Изогональная

Двойственная мозаика

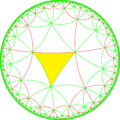
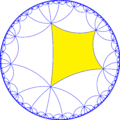
Двойственная созаика называется кис-ромбической мозаикой порядка 4-8, состоящей из полного разбиения восьмиугольной мозаики порядка 4?! [1]. На рисунке треугольники показаны с чередующимся цветом. Эта мозаика представляет фундаментальную треугольную область с симметрией [8,4] (*842).

Симметрия

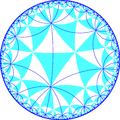
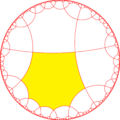
Усечённая четырёх-восьмиугольная мозаика *842, с зеркалами

Имеется 15 подгрупп, построенных из [8,4] путём удалением зеркального отражения и операцией альтернации^[англ.]. Зеркала могут быть удалены, если их порядки ветвей все чётны, что уменьшает порядок соседней ветви вдвое. Удаление двух зеркал оставляет точку вращения половинного порядка в месте пересечения зеркал. На рисунках фундаментальные области показаны чередующимся цветом, а зеркала находятся на границе между цветами. Подгруппа с индексом 8, [1⁺,8,1⁺,4,1⁺] (4242), является коммутантом группы [8,4].

Группа [8,4*], полученная из [8,4⁺] (4*4) удалением точек вращения, становится (*4444) или (*44), а другая группа [8*,4], полученная из [8+,4] (8*2) удалением точек вращения, становится (*22222222) или (*28). И их прямые подгруппы [8,4*]⁺, [8*,4]⁺ с индексами 16 и 32 соответственно могут быть заданы в орбифолдной нотации как (4444) и (22222222).

Подгруппы [8,4] (*842) малого порядка
Индекс	1	2			4
Диаграмма
Коксетер[англ.]	[8,4] =	[1+,8,4] =	[8,4,1+] = =	[8,1+,4] =	[1+,8,4,1+] =	[8+,4+]
Орбифолд[англ.]	*842	*444[англ.]*	*882[англ.]	*4222[англ.]	*4242[англ.]	42×
Semidirect subgroups
Диаграмма
Коксетер		[8,4+]	[8+,4]	[(8,4,2+)]	[8,1+,4,1+] = = = =	[1+,8,1+,4] = = = =
Орбифолд		4*4	8*2	2*42	2*44	4*22
Прямые подгруппы
Индекс	2	4			8
Диаграмма
Коксетер	[8,4]+ =	[8,4+]+ =	[8+,4]+ =	[8,1+,4]+ =	[8+,4+]+ = [1+,8,1+,4,1+] = = =
Орбифолд	842	444	882	4222	4242
Радикальные подгруппы
Индекс		8	16		32
Диаграмма
Коксетер		[8,4*] =	[8*,4]	[8,4*]+ =	[8*,4]+
Орбифолд		*4444	*22222222	4444	22222222

Связанные многогранники и мозаики

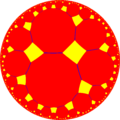
Исходя из построения Витхоффа существует четырнадцать гиперболических однородных мозаик, которые базируются на правильной восьмиугольной мозаике порядка 4.

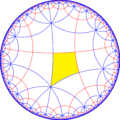
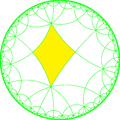
Если рисовать мозаики, выкрашивая красным цветом исходные грани, жёлтым цветом исходные вершины и синим цветом исходные рёбра, получим 7 форм с полной [8,4] симметрией и 7 с полусимметрией.

Однородные восьмиугольные/квадратные мозаики
[8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (и подсимметрия [(∞,4,∞,4)] (*4242) )
= = =	=	= = =	=	= =	=
{8,4}	t{8,4}	r{8,4}	2t{8,4}=t{4,8}	2r{8,4}={4,8}	rr{8,4}	tr{8,4}
Однордные двойственные
V84	V4.16.16	V(4.8)2	V8.8.8	V48	V4.4.4.8	V4.8.16
Альтернированные
[1+,8,4] (*444)	[8+,4] (8*2)	[8,1+,4] (*4222)	[8,4+] (4*4)	[8,4,1+] (*882)	[(8,4,2+)] (2*42)	[8,4]+ (842)
=	=	=	=	=	=
h{8,4}	s{8,4}	hr{8,4}	s{4,8}	h{4,8}	hrr{8,4}	sr{8,4}
Альтернированные двойственные
V(4.4)4	V3.(3.8)2	V(4.4.4)2	V(3.4)3	V88	V4.44	V3.3.4.3.8

*n42 симметрии общеусечённых мозаик: 4.8.2n

Симметрия *n42 [n,4]	Сферическая		Евклидова	Компактная гиперболическая				Паракомп.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]…	*∞42 [∞,4]
Общеусечённая фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Общеусечённые двойственные	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 мутации симметрий всеусечённых мозаик: 4.2n.2n
Симметрия *nn2 [n,n]	Сферическая		Евклидова	Компактная гиперболическая				Паракомпактная
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Рисунок
Конф.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Двойственная фигура
Конф.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

См. также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на плоскости^[англ.]