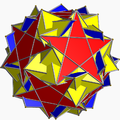
Однорідний зірчастий многогранник

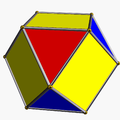
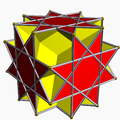
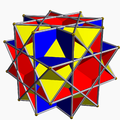
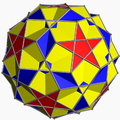
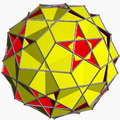
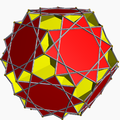
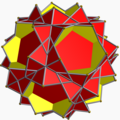
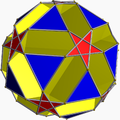
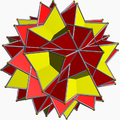
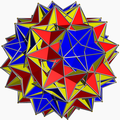
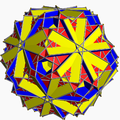
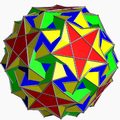
Однорі́дний зірча́стий многогра́нник — самоперетинний однорідний многогранник. Ці многогранники називають також неопуклими многогранниками, підкреслюючи наявність самоперетинів. Кожен многогранник може мати грані у вигляді зірчастих многокутників або зірчасті вершинні фігури, але може містити і те, й інше.

Вітрина з однорідними многогранниками в Музеї науки в Лондоні

Малий кирпатий ікосоікосододекаедр^[en] бувши однорідним зірчастим многогранником з вершинної фігурою 3⁵.⁵/₂

Повний набір 57 непризматичних однорідних зірчастих многогранників включає 4 правильних, званих тілами Кеплера — Пуансо, 5 квазіправильних, і 48 напівправильних.

Існує також дві нескінченні множини однорідних зірчастих призм і антипризм.

Так само, як (невироджені) зірчасті многокутники (які мають щільність^[en] більшу 1) відповідають круговим многокутникам з перекривними частинами, зірчасті многогранники, які не проходять через центр, мають щільність більшу 1, і відповідають сферичним многогранникам із перекривними частинами. Існує 48 таких непризматичних однорідних зірчастих многогранників. Решта 9 непризматичних однорідних зірчастих многогранників мають грані, що проходять через центр, є напівмногогранниками^[en] і не відповідають сферичним многогранникам, оскільки центр не можна однозначно спроєктувати на сферу.

Неопуклі форми будують із трикутників Шварца.

Всі трикутники, перераховані нижче, згруповано за їхніми групами симетрії, а всередині згруповано за розташуванням вершин.

Правильні многогранники позначено їхніми символами Шлефлі. Для інших, неправильних однорідних многогранників, зазначено їхню вершинну конфігурацію або номер однорідного многогранника (Uniform polyhedron index, U (1-80)).

Примітка: для неопуклих форм нижче наведено додатковий опис Неоднорідний, коли опукла оболонка набору вершин^[en] має таку ж топологію, але має неправильні грані. Наприклад, неоднорідне скошування (видалення ребер) може дати на місцях віддалених ребер прямокутник, а не квадрат.

Діедрична симетрія

Див. Призматичний однорідний многогранник.

Тетраедрична симетрія

Трикутники (3 3 2) на сфері

Існує один неопуклий вид, тетрагемігексаедр, який має тетраедричну симетрію (з фундаментальною областю трикутник Мебіуса (3 3 2)).

Існує два трикутники Шварца, з яких утворюються унікальні неопуклі однорідні многогранники — прямокутний трикутник (3/232) і один трикутник загального вигляду (3/233). Трикутник (3/2 3 3) генерує октагеміоктаедр^[en], наведений нижче в розділі октаедричної симетрії^[en].

Розташування вершин[en] (опукла оболонка)	Неопуклі види
Тетраедр
Спрямлений тетраедр Октаедр	(4.3/2.4.3) 3/2 3 | 2
Зрізаний тетраедр
Скошений тетраедр (кубооктаедр)
Всезрізаний тетраедр (зрізаний октаедр)
Кирпатий тетраедр (ікосаедр)

Октаедрична симетрія

Трикутники (4 3 2) на сфері

Існує 8 опуклих форм і 10 непуклих із октаедричною симетрією^[en] (з фундаментальною областю трикутник Мебіуса (4 3 2)).

Існує чотири трикутники Шварца, які утворюють неопуклі форми, два прямокутні, (3/2 4 2) і (4/3 3 2), і два загального вигляду, (4/3 4 3) та (3/2 4 4).

Розташування вершин[en] (опукла оболонка)	Неопуклі види
Куб
Октаедр
Кубооктаедр	(6.4/3.6.4)[en] 4/3 4 | 3	(6.3/2.6.3)[en] 3/2 3 | 3
Зрізаний куб	4.8/3.4/3.8/5)  2 4/3 (3/2 4/2)  |	(8/3.3.8/3.4)[en] 3 4 | 4/3	(4.3/2.4.4)[en] 3/2 4 | 2
Зрізаний октаедр
Ромбокубооктаедр	(4.8.4/3.8)[en] 2 4 (3/2 4/2) |	(8.3/2.8.4)[en] 3/2 4 | 4	(8/3.8/3.3)[en] 2 3 | 4/3
Неоднорідний зрізаний кубооктаедр	(4.6.8/3)[en] 2 3 4/3 |
Неоднорідний зрізаний кубооктаедр	(8/3.6.8)[en] 3 4 4/3 |
Кирпатий куб

Ікосаедрична симетрія

Трикутники (5 3 2) на сфері

Є 8 опуклих форм та 46 непуклих із ікосаедричною симетрією (з фундаментальною областю трикутник Мебіуса (5 3 2)) (або 47 неопуклих форм, якщо увести до складу багатогранник Скіллінга). Деякі неопуклі кирпаті види мають дзеркальну вершинну симетрію.

Розташування вершин[en] (опукла оболонка)	Неопуклі види
Ікосаедр	{5,5/2}	{5/2,5}	{3,5/2}
Неоднорідний зрізаний ікосаедр 2 5 |3	U37[en] 2 5/2 | 5	U61[en] 5/2 3 | 5/3	U67[en] 5/3 3 | 2	U73[en] 2 5/3 (3/2 5/4) |
Неоднорідний зрізаний ікосаедр 2 5 |3	U38[en] 5/2 5 | 2	U44[en] 5/3 5 | 3	U56[en] 2 3 (5/4 5/2) |
Неоднорідний зрізаний ікосаедр 2 5 |3	U32[en] | 5/2 3 3
Ікосододекаедр 2 | 3 5	U49[en] 3/2 3 | 5	U51[en] 5/4 5 | 5	U54 2 | 3 5/2	U70[en] 5/3 5/2 | 5/3	U71[en] 3 3 | 5/3	U36 2 | 5 5/2	U62[en] 5/3 5/2 | 3	U65[en] 5/4 5 | 3
Зрізаний додекаедр 2 3 | 5	U42[en]	U48[en]	U63[en]
Неоднорідний зрізаний додекаедр	U72[en]
Додекаедр	{5/2,3}	U30[en]	U41[en]	U47[en]
Ромбоікосододекаедр	U33[en]	U39[en]	U58[en]
Додекаедр зі знятими краями	U55[en]
Неоднорідний ромбоікосододекаедр	U31[en]	U43[en]	U50[en]	U66[en]
Неоднорідний ромбоікосододекаедр	U75[en]	U64[en]	Тіло Скіллінга[en] (див. нижче)
Неоднорідний ромбозрізаний ікосододекаедр	U45[en]
Неоднорідний ромбозрізаний ікосододекаедр	U59[en]
Неоднорідний зрізаний ікосододекаедр	U68[en]
Неоднорідний кирпатий додекаедр	U40[en]	U46[en]	U57[en]	U69[en]	U60[en]	U74

Тіло Скіллінга

Ще один неопуклий многогранник — великий бікирпатий біромбододекаедр^[en], відомий також як тіло Скіллінга, яке вершинно однорідне, але має спільні для граней пари ребер, так що чотири грані мають одне спільне ребро. Іноді його відносять до однорідних многогранників. Тіло має симетрію I_h^[en].

Вироджені випадки

Коксетер за допомогою побудови Вітгоффа визначив деяку кількість вироджених зірчастих многогранників, які мають ребра або вершини, що перекриваються. До цих вироджених форм належать:

• Малий складений ікосододекаедр^[en]
• Великий складений ікосододекаедр^[en]
• Малий складений ромбоікосододекаедр
• Складений ромбододекододекаедр
• Великий складений ромбоікосододекаедр

Див. також

• Зірчастий многокутник
• Список однорідних многогранників
• Список однорідних многогранників за породжувальними трикутниками Шварца