Top Qs
Timeline
Chat
Perspective
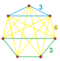
Rectified 5-cubes
From Wikipedia, the free encyclopedia
Remove ads
In five-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (October 2022) |
There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are located at the edge-centers of the 5-cube. Vertices of the birectified 5-cube are located in the square face centers of the 5-cube.
Remove ads
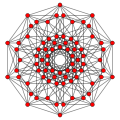
Rectified 5-cube
Summarize
Perspective
Alternate names
- Rectified penteract (acronym: rin) (Jonathan Bowers)
Construction
The rectified 5-cube may be constructed from the 5-cube by truncating its vertices at the midpoints of its edges.
Coordinates
The Cartesian coordinates of the vertices of the rectified 5-cube with edge length is given by all permutations of:
Images
Remove ads
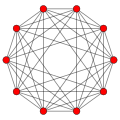
Birectified 5-cube
Summarize
Perspective
E. L. Elte identified it in 1912 as a semiregular polytope, identifying it as Cr52 as a second rectification of a 5-dimensional cross polytope.
Alternate names
- Birectified 5-cube/penteract
- Birectified pentacross/5-orthoplex/triacontiditeron
- Penteractitriacontiditeron (acronym: nit) (Jonathan Bowers)
- Rectified 5-demicube/demipenteract
Construction and coordinates
The birectified 5-cube may be constructed by birectifying the vertices of the 5-cube at of the edge length.
The Cartesian coordinates of the vertices of a birectified 5-cube having edge length 2 are all permutations of:
Images
Related polytopes
Remove ads
Related polytopes
These polytopes are a part of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads