Aro-teorio

Aro-teorio aŭ aroteorio (aŭ arteorio)^[1] estas branĉo de matematiko kreita ĉefe de la germana matematikisto Georg Cantor fine de la 19-a jarcento. Ĝi komence estis disputata, sed baldaŭ iĝis grava en la fundamenta teorio por difini bazajn matematikajn konceptojn kiel nombro, funkcio k.a.

Venn-a diagramo, kiu montras la komunaĵon de du aroj.

Komence oni evoluigis la t.n. naivan aroteorion, kiun oni povas difini jene:

La bazaj konceptoj de aroteorio estas aroj kaj membreco. Aro estas kolekto de objektoj nomataj membroj (aŭ elementoj) de la aro. La membroj povas esti ekzemple nombroj, funkcioj aŭ aroj mem. Oni difinas arojn per la ondkrampoj { kaj }. Tiel, {1,2} estas aro, kaj ankaŭ {1,2,3,4,...} (la nefinia aro de la naturaj nombroj kutime nomata N) kaj eĉ {2,3,N}, do la membroj ne devas esti de la sama klaso. Ankaŭ la malplena aro {} estas konsiderata valida aro.

Al tiaj aroj oni povas apliki diversajn operaciojn, kiel la kunaĵon kaj la komunaĵon.

Tamen montriĝis ke, se oni aplikas ĉiujn operaciojn senlime, aperas paradoksoj kiel la paradokso de Russell. Por solvi tiujn problemojn, oni rekonstruis la aroteorion, uzante aksioman metodon.

Historio

Georg Cantor.

La matematikaj aferoj plej ofte aperas kaj evoluas tra la interagado inter multaj esploristoj. La aroteorio, male, estis fondita per unusola artikolo en 1874 fare de Georg Cantor: nome Pri propreco de la kolekto de ĉiuj reelaj algebraj nombroj.^[2][3]

Ekde la 5-a jarcento a.K., dekomence el la greka matematikisto Zenono de Elajo en Okcidento kaj la unuaj hindiaj matematikistoj en Oriento, la matematikistoj estis baraktintaj kontraŭ la koncepto de infinito. Speciale elstara estas la laboro de Bernard Bolzano en la unua duono de la 19-a jarcento.^[4]​ La moderna kompreno de la infinito ekis en 1870-1874, kaj ĝi estis motivita de la verko de Cantor pri reela analizo.^[5]​ Kunsido en 1872 inter Cantor kaj Richard Dedekind influis sur la pensaro de Cantor, kio rezultis en la artikolo de Cantor de 1874.

La verko de Cantor polusigis dekomence la matematikistojn siaepokajn. Dum Karl Weierstrass kaj Dedekind apogis Cantor, Leopold Kronecker, konsiderata nuntempe kiel la fondinto de la matematika konstruismo, ne faris tion. La aroteorio de Cantor finfine ĝeneraliĝis, pro la utileco de la cantor-aj konceptoj, kiel la korespondo unu al unu inter aroj, lia pruvaro ke estas pl da reelaj nombroj ol entjeraj nombroj, kaj la "senfineco de senfinecoj" (la paradizo de Cantor) rezultanta de la operacio aro de potencoj. Tiu utileco de la aroteorio kondukis al la artikolo "Mengenlehre", havigita en 1898 de Arthur Schoenflies al la enciklopedio de Klein.

Russell en Trinity College en 1893.

La sekva tajdo de entuziasmo pri aroteorio okazis ĉirkaŭ 1900, kiam oni malkovris, ke kelkaj interpretoj de la aroteorio de Cantor kondukas al kontraŭdiroj, nome "antinomioj" aŭ paradoksoj. Bertrand Russell kaj Ernst Zermelo trovis sendepende la plej facilan kaj plej konatan paradokson, nuntempe nomatan Paradokso de Russell: oni konsideru "la aron de ĉiuj aroj, kiuj ne estas membroj de si mem", kio kondukas al kontraŭdiro, ĉar tiu devas esti samtempe membro de si mem kaj ne esti membro de si mem. En 1899, Cantor men estis stariginta la demandon "Kio estas la kardinala nombro de la aro de ĉiuj aroj?", kaj li atingis rilatan paradokson. Russell uzis sian paradokson kiel temon en sia revizio de la kontinenta matematiko de 1903 en sia verko "La principoj de la matematikoj".

En 1906, la britaj legantoj povis alveni al la libro "Theory of Sets of Points"^[6] fare de la geedzoj William Henry Young kaj Grace Chisholm Young, publikigita de Cambridge University Press.

La elano de la aroteorio estis tia ke la debato pri la paradoksoj ne kondukis al ĝia forlaso. La verkoj de Zermelo en 1908 kaj tiuj de Abraham Fraenkel kaj Thoralf Skolem en 1922 rezultis en la aro de aksiomoj ZFC, kiu iĝis la aro de aksiomoj plej uzata por la aroteorio. La laboro de analizistoj, kiel tiu de Henri Lebesgue, pruvis la grandan matematikan utilecon de la aroteorio, kiu ekde tiam iĝis fako de la moderna matematiko. La aroteorio estas uzata ofte kiel fonda sistemo, kvankam en kelkaj areoj - kiel la algebraj geometrio kaj topologio - oni konsideras, ke la teorio de kategorioj estas preferebla fundamento.

Ontologio

Komenca segmento de la hierarkio de von Neumann.

Aro estas pura, se ĉiuj ĝiaj membroj estas aroj, ĉiuj membroj de ĝiaj membroj estas aroj, ktp. Ekzemple, la aro enhavanta nur malplenan aron estas nemalplena pura aro. En moderna aroteorio, oftas limigi atenton al la "von Neumann-universo" de puraj aroj, kaj multaj sistemoj de aksioma aroteorio estas dezajnitaj por aksiomatigi nur la purajn arojn. Estas multaj teknikaj avantaĝoj por ĉi tiu restrikto, kaj malmulte da ĝeneraleco perdiĝis, ĉar esence ĉiuj matematikaj konceptoj povas esti modeligitaj per puraj aroj. Aroj en la von Neumann-universo estas organizitaj en akumulan hierarkion, surbaze de kiom profunde iliaj membroj, membroj de membroj, ktp., estas komprenataj. Ĉiu aro en ĉi tiu hierarkio estas asignita (per transfinia rikuro) ordonombro ${\displaystyle \alpha }$, konata kiel ĝia rango. La rango de pura aro ${\displaystyle X}$ estas difinita kiel la malplej orda kiu estas strikte pli granda ol la rango de iu ajn el ĝiaj elementoj. Ekzemple, la malplena aro ricevas rangon 0, dum la aro enhavanta nur la malplenan aron ricevas rangon 1. Por ĉiu orda ${\displaystyle \alpha }$, la aro ${\displaystyle V_{\alpha }}$ estas difinita por konsisti el ĉiuj puraj aroj kun rango malpli ol ${\displaystyle \alpha }$. La tuta "von Neumann-universo" estas indikita ${\displaystyle V}$.

Aplikoj

Multajj matematikaj konceptoj povas esti difinitaj precize uzante nur ar-teoriajn konceptojn. Ekzemple, matematikaj strukturoj tiom diversaj kiel grafeoj, sternaĵoj, ringoj, vektoraj spacoj, kaj rilataj algebroj povas ĉiuj difinitaj kiel aroj kiuj kontentigas variajn (aksiomajn) proprecojn. Ekvivalento kaj ordorilatoj estas ĉieaj en matematiko, kaj la teorio de matematikaj rilatoj povas esti priskribitaj en aro-teorio.^[7][8]

Principia Mathematica estas la plej grava verko de Isaac Newton. Tie startis la evoluo de la aro-teorio.

Aroteorio ankaŭ estas promesplena fundamenta sistemo por multo da matematiko. Ekde la publikigo de la unua volumo de Principia Mathematica, estis postulite ke la plej multaj (aŭ eĉ ĉiuj) matematikaj teoremoj povas esti derivitaj uzante trafe dezajnitan aron de aksiomoj por aroteorio, pliigita kun multaj difinoj, uzante unuan aŭ duaordan logikon. Ekzemple, ecoj de la naturaj kaj reelaj nombroj povas esti derivitaj ene de aroteorio, ĉar ĉiu el tiuj nombrosistemoj povas esti difinita reprezentante siajn elementojn kiel aroj de specifaj formoj.^[9]

Aro-teorio utilas kiel fundamento por matematika analizo, topologio, abstrakta algebro, kaj diskreta matematiko same estas nediskutebla; matematikistoj akceptas (principe) ke teoremoj en ĉi tiuj areoj povas esti derivitaj de la koncernaj difinoj kaj la aksiomoj de aroteorio. Tamen, restas ke malmultaj plenaj derivaĵoj de kompleksaj matematikaj teoremoj de aroteorio estis formale kontrolitaj, ĉar tiaj formalaj derivaĵoj ofte estas multe pli longaj ol la naturlingvaj pruvoj kiujn matematikistoj ofte prezentas. Unu konfirmprojekto, nome Metamath, inkludas hom-skribitajn, komputil-kontrolitajn derivaĵojn de pli ol 12 000 teoremoj komencantaj de Zermelo–Fraenkel aroteorio, unuaorda logiko kaj propozicia logiko.^[10]

Aksioma ar-teorio

Bildo pri la Aksiomo de elekto, kun indeksitaj familioj kiel kruĉoj kaj membroj kiel koloraj buletoj.

La aksiomoj por la aroteorio nuntempe plej ofte uzataj estas nomataj la Zermelo-Fraenkel-aksiomoj. Verdire, la aksiomoj estas ĉenoj de logikaj simboloj. Ĉi sube aperas iliaj "tradukoj" al natura lingvo:

1. Aksiomo de etendo: Du aroj estas samaj se kaj nur se ili havas la samajn membrojn.
2. Aksiomo de malplena aro: Ekzistas aro sen iuj ajn membroj. Oni skribas ĝin kiel {}.
3. Aksiomo de parigo: Se x kaj y estas aroj, tiam {x,y} estas aro, aro kiu havas nur x kaj y kiel siajn membrojn.
4. Aksiomo de kunigo: Por ĉiu aro x ekzistas aro y tiel ke la membroj de y estas precize la membroj de la membroj de x.
5. Aksiomo de senfineco: Ekzistas aro x tiel ke {} estas membro de x, kaj se y estas membro de x, tiam ankaŭ la kunaĵo y U {y} estas membro de x.
6. Aksiomo de apartigo: Se x estas aro kaj P(y) estas predikato, tiam ekzistas subaro de x kies membroj estas precize tiuj, por kiuj P(y) estas vera.
7. Aksiomo de anstataŭigo: Se x estas aro, kaj P(y,z) difinas bildigon (do P(y,z) kaj P(y,w) entenas z=w) tiam ekzistas aro enhavanta precize la bildojn de la membroj de x.
8. Aksiomo de potenca aro: Ĉiu aro havas potencan aron. Do, por ĉiu aro x ekzistas aro y tiel ke la membroj de y estas ĉiuj subaroj de x.
9. Aksiomo de reguleco: Ĉiu ne-malplena aro x havas membron y tiel ke x kaj y estas disaj aroj.
10. Aksiomo de elekto: Se x estas aro de reciproke disaj ne-malplenaj aroj, ekzistas aro y kiu enhavas precize unu membron de ĉiu membro de x.

La aksiomoj de reguleco kaj de elekto restas disputataj de malmultaj matematikistoj.

Studfakoj

Ar-teorio estas grava areo de esplorado en matematiko kun multaj interrilataj subfakoj:

Kombina ar-teorio

La teoremo de Ramsey malfermiĝis al la Kombina Ar-teorio.

Kombina ar-teorio temas pri etendoj de finia kombinatoriko por nefinitaj aroj. Tio inkludas la studon de kardinala aritmetiko kaj la studon de etendoj de la teoremo de Ramsey same kiel de la teoremo Erdős–Rado.

Priskriba ar-teorio

Priskriba ar-teorio estas la studo de subaroj de la reela linio kaj, pli ĝenerale, de subaroj de "Polaj spacoj". Ĝi komenciĝas kun la studo de punktoklasoj en la Borel-hierarkio kaj etendiĝas al la studo de pli kompleksaj hierarkioj kiel ekzemple la projekcia hierarkio kaj la Wadge-hierarkio. Multaj trajtoj de Borel-aroj povas esti establitaj en ZFC, sed pruvi tiujn trajtojn necesaj por pli komplikaj aroj postulas kromajn aksiomojn ligitajn al decidemo kaj grandaj kardinaloj.

La kampo de efika priskriba aroteorio estas inter aroteorio kaj rikura teorio. Ĝi inkludas la studon de lumfacaj punktoklasoj, kaj estas proksime rilatita al hiperaritmetika teorio. En multaj kazoj, rezultoj de klasika priskriba aroteorio havas efikajn versiojn; en kelkaj kazoj, novaj rezultoj estas akiritaj pruvante la efikan version unue kaj poste etendante ("relativigante") ĝin por igi ĝin pli larĝe aplikebla.

Lastatempa areo de esplorado koncernas Borel-ekvivalentajn rilatojn kaj pli komplikajn difineblajn ekvivalentrilatojn. Tio havas gravajn aplikojn al la studo de invariantoj en multaj subfakoj de matematiko.

Svaga ar-teorio

En aroteorio kiel Cantor difinis kaj Zermelo kaj Fraenkel aksiomatigis, objekto estas aŭ membro de aro aŭ ne. En svaga aroteorio tiu kondiĉo estis malstreĉita fare de Lotfi A. Zadeh, tiel ke objekto havas gradon da membreco en aro, nome nombro inter 0 kaj 1. Ekzemple, la grado de membreco de persono en la aro de "altaj homoj" estas pli fleksebla ol simpla jesa aŭ nea respondo kaj povas esti reala nombro kiel ekzemple 0,75.

Interna modelo de ar-teorio

(S_i) estas senfina indeksita familio de aroj indeksitaj super la reelaj nombroj R; tio estas, ekzistas aro S_i por ĉiu reela nombro i, kun malgranda specimeno montrita supre. Ĉiu aro enhavas almenaŭ unu, kaj eble senlime multajn, elementojn. La aksiomo de elekto permesas elekti ununuran elementon el ĉiu aro, formante korespondan familion de elementoj (x_i) ankaŭ indeksitaj super la reelaj nombroj, kun x_i desegnita de S_i. Ĝenerale, la kolektoj povas esti indeksitaj super iu aro I, (nomita indeksaro kies elementoj estas utiligitaj kiel indeksoj por elementoj en aro) ne nur R.

Interna modelo de Zermelo-Fraenkel ar-teorio (ZF) estas transitiva propra klaso kiu inkludas ĉiujn ordajn nombrojn kaj kontentigas ĉiujn aksiomojn de ZF. La kanona ekzemplo estas la konstruebla universo L evoluigita fare de Gödel. Unu kialo kial la studo de internaj modeloj estas interesaj estas ke ĝi povas esti uzita por pruvi konsekvencrezultojn. Ekzemple, povas esti montrite ke nekonsiderante ĉu modelo V de ZF kontentigas la kontinuuman hipotezon aŭ la aksiomon de elekto, la interna modelo L konstruita ene de la origina modelo kontentigos kaj la ĝeneraligitan kontinuuman hipotezon kaj la aksiomon de elekto. Tiel la supozo ke ZF estas konsekvenca (havas almenaŭ unu modelon) implicas ke ZF kune kun ĉi tiuj du principoj estas konsekvenca.

La studo de internaj modeloj estas ofta en la studo de persistemo kaj de grandaj kardinaloj, precipe dum pripensado de aksiomoj kiel ekzemple la aksiomo de persistemo, kiu kontraŭdiras la aksiomon de elekto. Eĉ se fiksa modelo de aroteorio kontentigas la aksiomon de elekto, eble interna modelo malsukcesus kontentigi la aksiomon de elekto. Ekzemple, la ekzisto de sufiĉe grandaj kardinaloj implicas ke ekzistas interna modelo kontentiganta la aksiomon de determineco (kaj tiel ne kontentiganta la aksiomon de elekto).^[11]

Grandaj kardinaloj

Granda kardinalo estas kardinala nombro kun kroma propreco. Multaj tiaj trajtoj estas studitaj, kiel ekzemple nealireblaj kardinaloj, mezureblaj kardinaloj, kaj multaj pli. Tiuj trajtoj tipe implicas, ke la kardinalo devas esti tre granda, kun la ekzisto de kardinalo kun la precizigita propreco nepruvebla en Zermelo-Fraenkel aroteorio.

Persistemo

Persistemo rilatas al la fakto ke, sub konvenaj supozoj, certaj du-ludantaj ludoj de perfektaj informoj estas determinitaj de la komenco en la senco ke unu ludanto devas havi venkan strategion. La ekzisto de tiuj strategioj havas gravajn sekvojn en priskriba aroteorio, ĉar la supozo ke pli larĝa klaso de ludoj estas determinita ofte implicas, ke pli larĝa klaso de aroj havos topologian proprecon. La aksiomo de determineco (AD, persistemo) estas grava studobjekto; kvankam malkongrua kun la aksiomo de elekto, AD, implicas ke ĉiuj subaroj de la reela linio estas bone kondutitaj (aparte, mezureblaj kaj kun la perfekta aro-posedaĵo). AD povas esti uzita por pruvi, ke la Wadge-gradoj havas elegantan strukturon.

Devigado

Paul Cohen inventis la metodon de devigado serĉante modelon de ZFC en kiu la kontinuumo-hipotezo malsukcesas, aŭ modelon de ZF en kiu la aksiomo de elekto malsukcesas. Devigo aldonas al iu antaŭfiksita modelo de aroteorio kromajn arojn por krei pli grandan modelon kun trajtoj determinitaj (t.e. "devigitaj") per konstruado kaj la origina modelo. Ekzemple, la konstruo de Cohen aldonas kromajn subarojn de la naturaj nombroj ne ŝanĝanta iujn ajn da la kardinalaj nombroj de la origina modelo. Devigado ankaŭ estas unu el du metodoj por pruvi relativan konsistencon per finitismaj metodoj, dum la alia metodo estas la Bule-valoraj modeloj.

Kardinalaj invariantoj

Fama problemo de Ar-teoria topologio estas la normala Moore-spaca demando, demando en ĝenerala topologio kiu estis la temo kaj celo de intensa esplorado. La respondo al la normala Moore-spac-demando estis poste pruvita sendepende de ZFC.

Kardinala invarianto estas eco de la reela linio mezurita per kardinala nombro. Ekzemple, bone studita invarianto estas la plej malgranda kardinaleco de kolekto de magraj aroj de reeloj, kies kuniĝo estas la tuta reela linio. Ĉi tiuj estas invariantoj en la senco ke ĉiuj du izomorfaj modeloj de aroteorio devas doni la saman kardinalon por ĉiu invarianto. Oni studis multajn kardinalajn invariantojn, kaj la rilatoj inter ili ofte estas kompleksaj kaj rilataj al aksiomoj de aroteorio.

Ar-teoria topologio

Ar-teoria topologio studas demandojn de ĝenerala topologio kiuj estas ar-teoria en naturo aŭ kiuj postulas progresintajn metodojn de ar-teorio por sia solvo. Multaj el tiuj teoremoj estas sendependaj de ZFC, postulante pli fortajn aksiomojn por sia pruvo. Fama problemo estas la normala Moore-spaca demando, demando en ĝenerala topologio kiu estis la temo kaj celo de intensa esplorado. La respondo al la normala Moore-spac-demando estis poste pruvita sendepende de ZFC.

Operacioj per aroj

Kunaĵo de du aroj

Kunaĵo

Pli detalaj informoj troveblas en artikolo Kunaĵo.

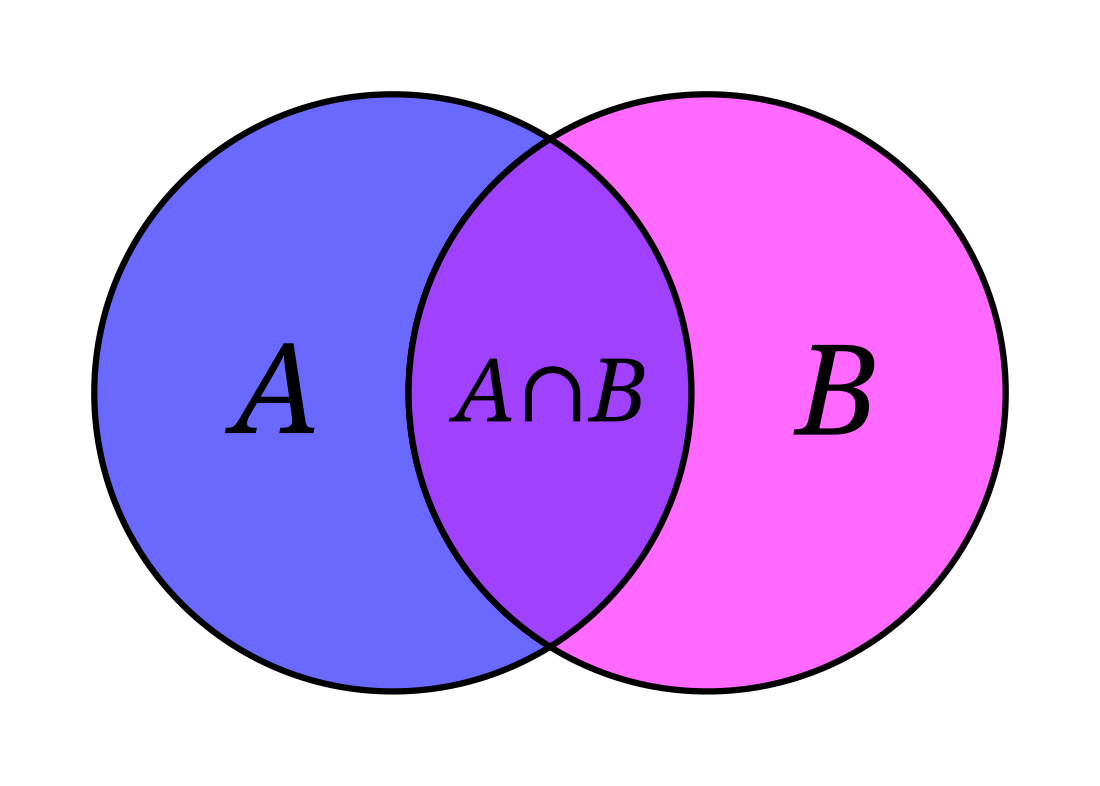
La kunaĵo de du aroj A kaj B konsistas el ĉiuj elementoj, kiuj estas en A, en B aŭ en ambaŭ. La operacio nature ĝeneraliĝas al pli ol du aroj; ĝi estas ĝeneraligebla ankaŭ al nefinie da aroj. Ĝi estas komuta kaj asocia. Oni notas ĝin per la kunigo-signo (∪), kiu similas al pelveto aŭ al litero "U".

Komunaĵo de du aroj

Komunaĵo

Pli detalaj informoj troveblas en artikolo Komunaĵo.

La komunaĵo de du aroj A kaj B konsistas el ĉiuj elementoj, kiuj estas kaj en A kaj en B. La operacio nature ĝeneraliĝas al pli ol du aroj; ĝi estas ĝeneraligebla ankaŭ al nefinie da aroj. Ĝi estas komuta kaj asocia. Oni notas ĝin per la komunaĵiga signo (∩), kiu similas al inversigita pelveto.

La kunigo kaj la komunaĵigo estas reciproke distribuecaj. La aroj do kun tiuj du operacioj formas latison.

Polemiko

De la komenco de aroteorio, kelkaj matematikistoj protestis kontraŭ ĝi kiel fundamento por matematiko. La plej ofta obĵeto kontraŭ aroteorio, esprimita de Leopold Kronecker en la plej fruaj jaroj de aroteorio, komenciĝas de la konstruisma rigardo ke matematiko estas loze rilata al komputado. Se ĉi tiu vidpunkto estas akceptita, tiam la traktado de senfinaj aroj, kaj en naiva kaj en aksioma aroteorio, enkondukas en matematikajn metodojn kaj objektojn kiuj ne estas komputeblaj eĉ principe. La farebleco de konstruismo kiel anstataŭa fundamento por matematiko estis tre pliigita per la influa libro de Errett Bishop nome Foundations of Constructive Analysis.^[12]

Malsama obĵeto prezentita fare de Henri Poincaré estas ke difini arojn uzantajn la aksiomajn skemojn de specifo kaj anstataŭigo, same kiel la aksiomon de potencoaro, enkondukas nediktivecon, specon de cirkleco, en la difinojn de matematikaj objektoj. La amplekso de predikative fondita matematiko, dum malpli ol tiu de la ofte akceptita Zermelo-Fraenkel-teorio, estas multe pli bonega ol tiu de konstruiva matematiko, ĝis la punkto ke Solomon Feferman diris ke, "ĉio el science uzebla analizo povas esti evoluigita [uzante predikativajn metodojn]".^[13]

Ludwig Wittgenstein kondamnis la ar-teorion filozofie pro ĝiaj konotacioj de matematika platonismo.

Ludwig Wittgenstein kondamnis la ar-teorion filozofie pro ĝiaj konotacioj de matematika platonismo.^[14] Li skribis ke "aroteorio estas malĝusta", ĉar ĝi konstruas sur la "sensencaĵo" de fikcia simboleco, havas "malutilajn idiomaĵojn", kaj ke estas sensence paroli pri "ĉiuj nombroj".^[15] Wittgenstein identigis matematikon kun algoritma homa dedukto;^[16] la bezono de certa fundamento por matematiko ŝajnis, al li, sensenca.^[17] Krome, ĉar homa fortostreĉo estas nepre finhava, la filozofio de Wittgenstein postulis ontologian engaĝiĝon al radikala konstruismo kaj finitismo. Meta-matematikaj deklaroj - kiuj, por Wittgenstein, inkludis ajnan deklaron kvantigantan super senfinaj domajnoj, kaj tiel super preskaŭ ĉiu moderna aroteorio - ne estas matematiko.^[18] Malmultaj modernaj filozofoj adoptis la opiniojn de Wittgenstein post sensacia eraro en Bemerkungen über die Grundlagen der Mathematik (Rimarkoj pri la Fundamentoj de Matematiko): Wittgenstein provis refuti la nekompletecajn teoremojn de Gödel leginte nur la resumon. Kiel recenzistoj Georg Kreisel, Bernays, Michael Dummett kaj R. L. Goodstein ĉiuj substrekis, multaj el liaj kritikoj ne validis por la publikaĵo entute. Nur lastatempe filozofoj kiel Crispin Wright komencis rehabiliti la argumentojn de Wittgenstein.^[19]

Kategoriteoriuloj proponis topos-teorion kiel alternativon al la tradicia aksioma aroteorio. Topos-teorio povas interpreti diversajn alternativojn al tiu teorio, kiel konstruismo, finhava aroteorio kaj komputebla aroteorio.^[20][21] Topos ankaŭ donas naturan agordon por devigado kaj studoj pri la sendependeco de elekto de ZF, same kiel disponigante la kadron por sencela topologio kaj Stone spacoj.^[22]

Aktiva areo de esplorado estas la unuvalentaj fundamentoj kaj rilata al ĝi homotopia tipo-teorio. Ene de homotopia tipoteorio, aro povas esti rigardita kiel homotopia 0-speca, kun universalaj trajtoj de aroj ekestiĝantaj de la induktaj kaj rikursaj trajtoj de pli altaj induktaj tipoj. Principoj kiel ekzemple la aksiomo de elekto kaj la leĝo de la ekskludita mezo povas esti formulitaj en maniero koresponda al la klasika formuliĝo en aroteorio aŭ eble en spektro de apartaj manieroj unikaj al tipteorio. Kelkaj el tiuj principoj povas esti pruvitaj kiel sekvo de aliaj principoj. La vario de formuligoj de tiuj aksiomaj principoj ebligas detalan analizon de la formuligoj necesaj por derivi diversajn matematikajn rezultojn.^[23][24]

Bildaro

• 
  ${\displaystyle A\subseteq B}$
• 
  Komenca segmento de la hierarkio de von Neumann