フィボナッチ数

フィボナッチ数（フィボナッチすう、英: Fibonacci number）は、イタリアの数学者レオナルド・フィボナッチ（ピサのレオナルド）に因んで名付けられた数である。

フィボナッチ数を一辺とする正方形

概要

フィボナッチ数列（フィボナッチすうれつ、（英: Fibonacci sequence） (F_n) は、次の漸化式で定義される：

${\displaystyle {\begin{cases}F_{0}=0&\,\\F_{1}=1&\,\\F_{n}=F_{n-1}+F_{n-2}&(n\geqq 2)\end{cases}}}$

第0～22項の値は次の通りである：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …（オンライン整数列大辞典の数列 A000045）

1202年にフィボナッチが発行した『算盤の書（Liber Abaci）』に記載されたことで「フィボナッチ数」と呼ばれているが、それ以前にもインドの学者であるヘーマチャンドラ（Hemachandra）が韻律の研究により発見し、書物に記したことが判明している^[1][2]。

兎の問題

レオナルド・フィボナッチは次の問題を考案した^[3]。

• 1つがいの兎は、産まれて2か月後から毎月1つがいずつの兎を産む。
• 兎が死ぬことはない。
• この条件の下で、産まれたばかりの1つがいの兎は1年の間に何つがいの兎になるか？

つがいの数は次の表のようになる。どの月のつがいの合計も、その前の2つの月での合計の和となり、フィボナッチ数が現れていることが分かる。

	産まれたばかりのつがい	生後1か月のつがい	生後2か月以降のつがい	つがいの数（合計）
0か月後	1	0	0	1
1か月後	0	1	0	1
2か月後	1	0	1	2
3か月後	1	1	1	3
4か月後	2	1	2	5
5か月後	3	2	3	8
6か月後	5	3	5	13
7か月後	8	5	8	21
8か月後	13	8	13	34
9か月後	21	13	21	55
10か月後	34	21	34	89
11か月後	55	34	55	144
12か月後	89	55	89	233

一般項

フィボナッチ数列の一般項は次の式で表される^[3]：

${\displaystyle F_{n}={\frac {1}{\sqrt {5}}}\left\{\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right\}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}}$

この式は1843年にビネ（Jacques Philippe Marie Binet）が発表したことからビネの公式と呼ばれるが、それ以前の1730年（ド・モアブル）・1765年（オイラー）にも発表されており、ビネは最初の発見者ではない。

なお、この式に現れる

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988749894\cdots }$

は黄金数で、いくつかの数学的特徴がある。黄金数を作る二次方程式 x² − x − 1 = 0 の解を α, β (α > β) とすると、上記の一般項は

${\displaystyle F_{n}={\frac {\alpha ^{n}-\beta ^{n}}{\alpha -\beta }}={\frac {\alpha ^{n}}{\alpha -\beta }}+{\frac {\beta ^{n}}{\beta -\alpha }}}$

と表せる。

また、一般項の第2項 1/ √5 (−φ)⁻ⁿ の絶対値は減少列で、n = 0 のとき 1/ √5 = 0.447... < 1/2 より、第2項を切り捨てた式は F_n の値を 0.447 以下（n > 4 のとき1%以下）の誤差で与える近似式である。

${\displaystyle F_{n}\fallingdotseq {\frac {\varphi ^{n}}{\sqrt {5}}}}$

この誤差の絶対値は0.5未満なので、F_n の正確な整数値は以下の式で得られる^[3]。

${\displaystyle F_{n}=\left\lfloor {\frac {\varphi ^{n}}{\sqrt {5}}}+{\frac {1}{2}}\right\rfloor =\left\lfloor {\frac {1}{\sqrt {5}}}\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}+{\frac {1}{2}}\right\rfloor }$

ただし、⌊ x ⌋ は床関数である。

なお、後述の負数番への拡張を考慮した場合、n < 0 では逆に一般項の第1項の絶対値が0.5未満となるため、n < 0 における F_n の正確な整数値は以下の式で得られる。

${\displaystyle F_{n}=-\left\lfloor {\frac {(-\varphi )^{-n}}{\sqrt {5}}}+{\frac {1}{2}}\right\rfloor =-\left\lfloor {\frac {1}{\sqrt {5}}}\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}+{\frac {1}{2}}\right\rfloor }$

これらのことから、任意の整数 n における F_n の正確な整数値は以下の式で得られる。

${\displaystyle F_{n}=(\operatorname {sgn} n)\left\lfloor {\frac {\{(\operatorname {sgn} n)\varphi \}^{|n|}}{\sqrt {5}}}+{\frac {1}{2}}\right\rfloor =(\operatorname {sgn} n)\left\lfloor {\frac {1}{\sqrt {5}}}\left\{{\frac {1+(\operatorname {sgn} n){\sqrt {5}}}{2}}\right\}^{n}+{\frac {1}{2}}\right\rfloor }$

ただし、sgn x は符号関数である。

行列表現

また、フィボナッチ数列の漸化式は次のように行列表現できる^[3]：

${\displaystyle {\begin{bmatrix}F_{n+1}\\F_{n}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}{\begin{bmatrix}F_{n}\\F_{n-1}\end{bmatrix}},\;\;{\begin{bmatrix}F_{n}\\F_{n-1}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}{\begin{bmatrix}F_{n-1}\\F_{n-2}\end{bmatrix}}}$

これらを並べて表記すると、

${\displaystyle {\begin{aligned}{\begin{bmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{bmatrix}}&={\begin{bmatrix}1&1\\1&0\end{bmatrix}}{\begin{bmatrix}F_{n}&F_{n-1}\\F_{n-1}&F_{n-2}\end{bmatrix}}\\&={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{2}{\begin{bmatrix}F_{n-1}&F_{n-2}\\F_{n-2}&F_{n-3}\end{bmatrix}}\\&=\cdots \\&={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}{\begin{bmatrix}F_{1}&F_{0}\\F_{0}&F_{-1}\end{bmatrix}}\\&={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}{\begin{bmatrix}1&0\\0&1\end{bmatrix}}\end{aligned}}}$

${\displaystyle \therefore {\begin{aligned}{\begin{bmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}\end{aligned}}}$

ここで、F₋₁ = 1 は、漸化式 F_n = F_n−1 + F_n−2 に n = 1 を代入すると得られる（詳細は後述の負数番への拡張を参照）。

更に、n を 2n で置換すると、

${\displaystyle {\begin{aligned}{\begin{bmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{bmatrix}}&={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{2n}=\left({\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}\right)^{2}={\begin{bmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{bmatrix}}^{2}\\&={\begin{bmatrix}{F_{n}}^{2}+{F_{n+1}}^{2}&(F_{n-1}+F_{n+1})F_{n}\\(F_{n-1}+F_{n+1})F_{n}&{F_{n-1}}^{2}+{F_{n}}^{2}\end{bmatrix}}\end{aligned}}}$

よって、

${\displaystyle {\begin{aligned}F_{2n+1}&={F_{n}}^{2}+{F_{n+1}}^{2}\\F_{2n}&=(F_{n-1}+F_{n+1})F_{n}=(2F_{n-1}+F_{n})F_{n}=(2F_{n+1}-F_{n})F_{n}\\F_{2n-1}&={F_{n-1}}^{2}+{F_{n}}^{2}\end{aligned}}}$

母関数は

${\displaystyle g(x)=\sum \limits _{n=0}^{\infty }F_{n}x^{n}={\dfrac {x}{1-x-x^{2}}}}$

である。

また、この行列表現を基に、以下のような漸化式を考えることができる。

${\displaystyle {\begin{cases}F_{0}=0&\,\\F_{1}=1&\,\\F_{n}={F_{q}}^{2}+\{1+(-1)^{n}\}F_{q-1}F_{q}+{\dfrac {1-(-1)^{n}}{2}}{F_{q+1}}^{2}&\left(n\geqq 2,\;q=\left\lfloor {\dfrac {n}{2}}\right\rfloor \right)\end{cases}}}$

性質

フィボナッチ数列の隣接2項の商は黄金数 φ に収束する。この性質は初期値 (F₀ = 0, F₁ = 1) に依らない。

${\displaystyle \lim _{n\to \infty }{\frac {F_{n}}{F_{n-1}}}=\varphi }$

これは次のように導出される：

${\displaystyle x=\lim _{n\to \infty }{\frac {F_{n}}{F_{n-1}}}}$ が収束するとすれば、

${\displaystyle x=\lim _{n\to \infty }{\frac {F_{n-1}+F_{n-2}}{F_{n-1}}}=\lim _{n\to \infty }\left(1+{\frac {1}{F_{n-1}/F_{n-2}}}\right)=1+{\frac {1}{x}}}$

${\displaystyle x^{2}-x-1=0}$

• 自然数 p, q の最大公約数を r とすると、F_p と F_q の最大公約数は F_r である。

これより以下を導くことができる。

• m が n で割り切れるならば、F_m は F_n で割り切れる。
• 連続する2数は互いに素であることより、隣り合うフィボナッチ数も互いに素である。
• F_m が偶数となるのは m が 3 の倍数となるときと一致する。
• F_m が 5 の倍数となるのは m が 5 の倍数となるときと一致する。
• p が 2 でも 5 でもない素数のとき、m = p − (5/p) とおくと p は F_m を割り切る。ここで ( / ) はルジャンドル記号である。

フィボナッチ数の累和や累積について以下の式が成り立つ。

• F₁ + F₂ + F₃ + … + F_n = F_n+2 − 1
• F₁ + F₃ + F₅ + … + F_2n−1 = F_2n
• F₂ + F₄ + F₆ + … + F_2n = F_2n+1 − 1
• F₁² + F₂² + F₃² + … + F_n² = F_n F_n+1
• F_n−1 F_n+1 − F_n² = (−1)ⁿ

また、次の関係式が知られている。

${\displaystyle \sum _{k=1}^{\infty }{\frac {F_{k}}{n^{k}}}={\frac {n}{n^{2}-n-1}}}$

フィボナッチ数のうち平方数であるのは F₁ = F₂ = 1, F₁₂ = 144 のみ（Cohn 1964）^[4]、立方数であるのは F₁ = F₂ = 1, F₆ = 8 のみ（London and Finkelstein 1969）^[5]である。フィボナッチ数のうち累乗数であるのはこれしかない（Bugeaud, Mignotte, Siksek 2006）^[6]。（オンライン整数列大辞典の数列 A227875）

フィボナッチ数で素数であるのは 2, 3, 5, 13, 89, 233, 1597, 28657, … である（オンライン整数列大辞典の数列 A005478）。また、これらはフィボナッチ素数と呼ばれる。

フィボナッチ数で三角数であるのは 1, 3, 21, 55（オンライン整数列大辞典の数列 A039595）のみであることは Vern Hoggatt によって予想されていたが、のちに Luo Ming によって証明された^[7]。

フィボナッチ数でハーシャッド数であるのは 1, 2, 3, 5, 8, 21, 144, 2584, …（オンライン整数列大辞典の数列 A117774）。

フィボナッチ数は完全数にはならない^[8]。より一般に、フィボナッチ数は倍積完全数にもならず^[9]、2つのフィボナッチ数の商も完全数にはならない^[10]。

フィボナッチ数列の逆数和は収束し、記号 ψ で表される。

${\displaystyle \psi =\sum _{n=1}^{\infty }{\frac {1}{F_{n}}}={\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+\cdots =3.35988566\cdots }$^[11]

この ψ が無理数であることは証明されているが (André-Jeannin 1989)、超越数であるかどうかは分かっていない。

任意の正の整数は、1つ以上の連続しない相異なるフィボナッチ数の和として一意に表すことができる（ゼッケンドルフの定理）。

パスカルの三角形で数字を桂馬跳びのように拾うと、総和がフィボナッチ数になる数列が現れる。

また n が十分に大きいとき、フィボナッチ数列の漸化式を遡らせるとパスカルの三角形が現れ、桂馬跳びに同じ項が現れる。

パスカルの三角形の各々の底辺角に等分割線を加筆し、線上の数を合計していくと、フィボナッチ数列が現れる。

${\displaystyle F_{n}=F_{n-1}+F_{n-2}=F_{n-2}+2F_{n-3}+F_{n-4}=F_{n-3}+3F_{n-4}+3F_{n-5}+F_{n-6}}$

プログラミング言語での実装

再帰的処理の例としてよく紹介される。以下はPythonでの例。

ただし、下記実装例の内、#負数番への拡張に対応しているのは例5・例6のみである。

例1（再帰的処理による実装例）

このプログラムでは、n が与えられてから F_n が求まるまでに F_n ∝ φⁿ 回の関数呼び出しが発生する（すなわち指数時間の計算となる）ため、実用的ではない。したがって通常は、線形時間で計算するためにメモ化などの手法を用いる他、後述するように様々な実装例が検討されている。

def fib(n: int) -> int:
    if n < 2:
        return n
    else:
        return fib(n=n-1) + fib(n=n-2)

メモ化の例を挙げると^{[注釈 1]}、

from functools import cache

@cache
def fib(n: int) -> int:
    if n < 2:
        return n
    else:
        return fib(n=n-1) + fib(n=n-2)

例2（ループ処理による実装例）

def fib(n: int) -> int:
    a, b = 1, 0
    for _ in range(n):
        a, b = b, a+b
    return b

例3（指数関数的なコールを必要としない再帰的処理による実装例）

n が1以上の場合に第2・第3の引数を上記例2と同じ要領で順次更新していくことで、コール回数を n 回に抑えられる為、線形時間で処理できる。

def fib(n: int, a: int = 1, b: int = 0) -> int:
    if n == 0:
        return b
    else:
        return fib(n=n-1, a=b, b=a+b)

例4（対数時間での再帰的処理による実装例）

#行列表現で導出した漸化式（以下に再掲）を用いることで、再帰的処理でも対数時間で処理できる。

${\displaystyle {\begin{cases}F_{0}=0&\,\\F_{1}=1&\,\\F_{n}={F_{q}}^{2}+\{1+(-1)^{n}\}F_{q-1}F_{q}+{\dfrac {1-(-1)^{n}}{2}}{F_{q+1}}^{2}&\left(n\geqq 2,\;q=\left\lfloor {\dfrac {n}{2}}\right\rfloor \right)\end{cases}}}$

ただし、プログラム上は0を掛けるからと言ってその対象の値が計算されない訳では無い為（短絡評価されない）、条件式による分岐で表記している。

def fib(n: int) -> int:
    if n < 2:
        return n
    q = n // 2
    fq = fib(n=q)
    return fq ** 2 + (2 * fib(n=q-1) * fq if n % 2 == 0 else fib(n=q+1) ** 2)

例5（一般項による実装例）

浮動小数点型を使用すると計算誤差が発生する為、decimalモジュールを用いている^{[注釈 2]}。

from decimal import Decimal

SQRT5 = Decimal(5).sqrt()
PHI = (1 + SQRT5) / 2 # 黄金数

def fib(n: int) -> int:
    return round((PHI ** n - (-PHI) ** -n) / SQRT5)

なお、先述の通りフィボナッチ数列の一般項は、引数 n の符号によって2項の内いずれかが0.5未満となることから、符号関数及び床関数を用いて以下のように表すことができた。

${\displaystyle F_{n}=(\operatorname {sgn} n)\left\lfloor {\frac {\{(\operatorname {sgn} n)\varphi \}^{|n|}}{\sqrt {5}}}+{\frac {1}{2}}\right\rfloor }$（#一般項より再掲）

このことから、以下のように実装することで冪乗演算の回数を減らすことが出来る^{[注釈 3]}。

from decimal import Decimal

ONE = Decimal(1)
SQRT5 = Decimal(5).sqrt()
PHI = (1 + SQRT5) / 2 # 黄金数

def fib(n: int) -> int:
    if n == 0:
        return 0
    sgn_n = ONE.copy_sign(n)
    return sgn_n * round((sgn_n * PHI) ** abs(n) / SQRT5)

例6（行列表現での実装例）

${\displaystyle {\begin{bmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}}$（#行列表現より再掲）

より、n を n − 1 に置換すると、

${\displaystyle {\begin{bmatrix}F_{n}&F_{n-1}\\F_{n-1}&F_{n-2}\end{bmatrix}}={\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n-1}}$

従って、F_n は、上式右辺（の具体的な計算値）の左上成分に等しい。

行列の冪を簡潔に記述する為にSymPyを用いた^{[注釈 4][注釈 5]}。

from sympy import Matrix

def fib(n: int) -> int:
    return (Matrix([[1, 1], [1, 0]]) ** (n - 1))[0, 0] # 左上成分

その他の話題

フィボナッチ数列の螺旋。

ヒマワリの種は螺旋状に並んでおり、螺旋の数を数えていくとフィボナッチ数が現れる^[12]

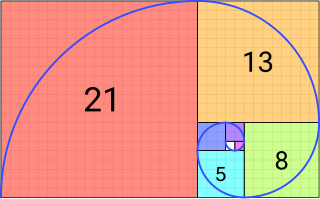
• フィボナッチ数は自然界の現象に数多く出現する。
• また、フィボナッチ数列が生み出す螺旋は、世界で最も美しい螺旋だと言われている。

ヨハネス・ケプラーは1611年に発表した小論文「新年の贈り物あるいは六角形の雪について」において、フィボナッチ数を自己を増殖する比例と呼び、植物の種子の能力の現れであると論じた^[13]。

• 花びらの数はフィボナッチ数であることが多い。^[要出典]
• フィボナッチ数は、花びらの枚数も決めているらしい。（『聖なる幾何学』p63より）
  • 3枚：ユリ、アヤメ、エンレイソウ
  • 5枚：オダマキ、サクラソウ、キンボウゲ、ノイバラ、ヒエンソウ
  • 8枚：デルフィニウム属、サンギナリア、コスモス
  • 13枚：シネラリア、コーンマリゴールド
  • 21枚：チコリー、オオハンゴンソウ
  • 34枚：オオバコ、シロバナムシヨケギク
  • 55枚：ユウゼンギク
  • 89枚：ミケルマス・デイジー
    • 花弁の数が144に達することはない。この数は、他の自然界に見られるフィボナッチ数の例でも限界になっていることが多い^[14]。

• アブラナやダイコンの花びらは4枚であり、植物学では花式図より3数性、4数性、5数性で分類される^[15][16]。
• 植物の花や実に現れる螺旋の数もフィボナッチ数であることが多い。
  • ヒマワリの螺旋の数はフィボナッチ数とされることもあるが、螺旋の数が多い場合、中心から離れると螺旋の隙間にも種ができてしまうため、途中から枝分かれしてフィボナッチ数にならないこともある^[17]。
• パイナップルの螺旋の数は時計回りは13、反時計回りは8になっている。
• 葉序（植物の葉の付き方）はフィボナッチ数と関連している。(シンパー=ブラウンの法則)
• らせん葉序におけるシンパー・ブラウンの法則はフィボナッチ数列と関連するが、「近似値を示すにすぎず、またこれにあてはまらない例もある」（岩波生物学辞典）。
• ハチやアリなど、オスに父親がない家系を辿っていくとフィボナッチ数列が現れる（父母2匹、祖父母3匹、曽祖父母5匹、高祖父母8匹…）。
• n 段の階段を1段または2段ずつ登るときに、登る場合の数は F_n+1 通りある。
• ●と○を合わせて n 個並べる。●が2個以上続かないように一列に並べる方法は F_n+2 通りある。
• 為替などのテクニカル分析で、フィボナッチ・リトレースメントという手法がよく使われている。

負数番への拡張

フィボナッチ数列は、漸化式 F_n = F_n−1 + F_n−2 を全ての整数 n に対して適用することにより、n が負の整数の場合に拡張できる。そして F_−n = (−1)ⁿ⁺¹F_n が成り立つ。この式より、負の番号の項は次のようになる。

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Fn	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765
F−n	0	1	−1	2	−3	5	−8	13	−21	34	−55	89	−144	233	−377	610	−987	1597	−2584	4181	−6765

類似の数列

フィボナッチ数列の定義である初期値や漸化式をやや変更して、類似の数列が作れる。

項数の変更

フィボナッチ数列は各項が先行する二項の和であるものであったが、それを「先行する k 項の和」と置き換えた一般化

${\displaystyle F_{n+k}^{(k)}:=F_{n+k-1}^{(k)}+F_{n+k-2}^{(k)}+\dotsb +F_{n}^{(k)}\quad (n\geq 0)}$

を考えることができる。ただし、初期値は 1 で埋める（1-fil型）

${\displaystyle F_{0}^{(k)}=F_{1}^{(k)}=\dotsb =F_{k-1}^{(k)}=1}$

あるいは 0 で埋める（0-fil型）

${\displaystyle F_{0}^{(k)}=F_{1}^{(k)}=\dotsb =F_{k-2}^{(k)}=0,\quad F_{k-1}^{(k)}=1}$

などを取るのが一般的である。これらフィボナッチ数列の類似物を、項数 k に対応するラテン語またはギリシャ語に由来する倍数接頭辞を「フィボナッチ」と組み合わせた名称で呼ぶ^{[注釈 6]}。

和の項数や初期値の変更

k	接頭辞[18]	名称	整数列大辞典
3	tri-	トリボナッチ数	0 fil: A000073 1 fil: A000213
4	tetra-	テトラナッチ数	0 fil: A000078 1 fil: A000288
5	penta-	ペンタナッチ数	0 fil: A001591 1 fil: A000322
6	hexa-	ヘキサナッチ数	0 fil: A001592 1 fil: A000383
7	hepta-	ヘプタナッチ数	0 fil: A122189 1 fil: A060455
8	octa-	オクタナッチ数	0 fil: A079262 1 fil: A123526
9	nona-	ノナ（ボ）ナッチ数	1 fil: A127193
10	deca-	デカ（ボ）ナッチ数	1 fil: A127194
11	undeca-	ウンデカ（ボ）ナッチ数	1 fil: A127624
12	dodeca-	ドデカ（ボ）ナッチ数	1 fil: A207539
20	icosa-	イコサナッチ数	⋮

トリボナッチ数

特に直前の三項の和として各項が定まるトリボナッチ数列は、フィボナッチ数列に次いでよく調べられている。0-fil型でオフセットが0番目からのものは

T₀ = T₁ = 0, T₂ = 1,

T_n+3 = T_n + T_n+1 + T_n+2 (n ≥ 0)

と表される。第0～21項の値は次の通りである：

0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, …（OEIS A000073）

トリボナッチ数列の一般項は次で表される。

${\displaystyle T_{n}={\frac {\alpha ^{n}}{(\alpha -\beta )(\alpha -\gamma )}}+{\frac {\beta ^{n}}{(\beta -\gamma )(\beta -\alpha )}}+{\frac {\gamma ^{n}}{(\gamma -\alpha )(\gamma -\beta )}}}$

ただし、α, β, γ は三次方程式 x³ − x² − x − 1 = 0 の3解

${\displaystyle {\begin{aligned}\alpha &={\frac {1}{3}}\left(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\\\beta &={\frac {1}{3}}\left(1+\omega {\sqrt[{3}]{19-3{\sqrt {33}}}}+{\bar {\omega }}{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\\\gamma &={\frac {1}{3}}\left(1+{\bar {\omega }}{\sqrt[{3}]{19-3{\sqrt {33}}}}+\omega {\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\end{aligned}}}$

であり、ここで

${\displaystyle \omega ={\frac {-1+{\sqrt {3}}i}{2}}}$（1 の虚立方根）

である。

また、上記の α をトリボナッチ定数という。これはフィボナッチ数列における黄金数に当たる定数で、トリボナッチ数列の隣接2項間の商はトリボナッチ定数に収束する：

${\displaystyle \lim _{n\to \infty }{\frac {T_{n}}{T_{n-1}}}=\alpha =1.839286755214161\cdots }$

パスカルの三角錐の n 段目の三角形の数字を桂馬跳びに拾って合計すると 2n-1 個の数から成る数列ができる。この数列を上から三角形状に並べ、数字を桂馬跳びに拾って合計するとトリボナッチ数が現れる。 また n が十分に大きいとき、トリボナッチ数列の漸化式を遡らせると中間の三角形が現れ、桂馬跳びに同じ項が現れる。

${\displaystyle T_{n}=T_{n-1}+T_{n-2}+T_{n-3}=T_{n-2}+2T_{n-3}+3T_{n-4}+2T_{n-5}+T_{n-6}=T_{n-3}+3T_{n-4}+6T_{n-5}+7T_{n-6}+6T_{n-7}+3T_{n-8}+T_{n-9}}$

テトラナッチ数

直前の四項の和に変更したテトラナッチ数列も同様に様々なことが知られている。同様にオフセット0番の 0-fil型は

T₀ = T₁ = T₂ = 0, T₃ = 1,

T_n+4 = T_n + T_n+1 + T_n+2 + T_n+3 (n ≥ 0)

と書けて、第0～21項の値は次の通りである：

0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, 76424, …（OEIS A000078）

一般項は、四次方程式 x⁴ − x³ − x² − x − 1 = 0 の4解を α, β, γ, δ として、

${\displaystyle T_{n}={\frac {\alpha ^{n}}{(\alpha -\beta )(\alpha -\gamma )(\alpha -\delta )}}+{\frac {\beta ^{n}}{(\beta -\gamma )(\beta -\delta )(\beta -\alpha )}}+{\frac {\gamma ^{n}}{(\gamma -\delta )(\gamma -\alpha )(\gamma -\beta )}}+{\frac {\delta ^{n}}{(\delta -\alpha )(\delta -\beta )(\delta -\gamma )}}}$

となる。

初期値の変更

リュカ数

フィボナッチ数列の最初の2項を 2, 1 に置き換えた数列の項をリュカ数という。

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, …（OEIS A000032）

この数列の一般項は

${\displaystyle L_{n}=\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}+\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}=\varphi ^{n}+(1-\varphi )^{n}={\varphi ^{n}+(-\varphi )^{-n}}}$

と表される。

フィボナッチ数列やリュカ数の列を一般化したものがリュカ数列であり、1878年にエドゥアール・リュカが体系的な研究を行い、1913年にロバート・ダニエル・カーマイケル（英語版）がその結果を整理、拡張した^[19]。これらの研究が現代のフィボナッチ数の理論の基礎となった。