トップQs
タイムライン
チャット
視点
完全数
自分自身を除く正の約数の総和と、自分自身が等しい自然数 ウィキペディアから
Remove ads
完全数(かんぜんすう、英: perfect number)とは、自分自身を除く正の約数の和が自分自身に等しくなる自然数のことである。完全数は素数ではあり得ず、合成数に限られる。完全数の最初の4個は 6 (= 1 + 2 + 3)、28 (= 1 + 2 + 4 + 7 + 14)、496 (= 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248)、8128 (= 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064) である。
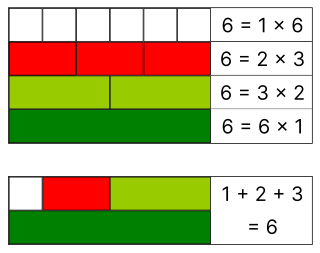
「完全数」は「万物は数なり」と考えたピタゴラスが名付けた数の一つであることに由来する[1]が、彼がなぜ「完全」と考えたのかについては何も書き残されていないようである[1]。紀元1世紀ごろは、全ての数は過剰数と不足数と完全数の3種類に分けられて、道徳的な意味付けが真剣に考えられた[2]。中世の『聖書』の研究者は、「6 は『神が世界を創造した(天地創造)6日間』、28 は『月の公転周期』で、これら2つの数は地上と天界における神の完全性を象徴している」[1]と考えたとされる[3]。古代ギリシアの数学者は他にもあと2つの完全数 (496, 8128) を知っていた[1]。以来、完全数はどれだけあるのかの探求が2500年以上のちの現在まで続けられている。
完全数の定義は、正の約数の総和が自分自身の2倍に等しいことと同値である。すなわち、N が完全数であるとは、約数関数 σ に対して σ(N) = 2N が成り立つことであると表現できる。また、正の約数の逆数和が 2 であると表現することもできる。
Remove ads
歴史
完全数に関する数学上の最初の成果は紀元前3世紀ごろのユークリッドによってもたらされた。彼は『原論』(第9巻、命題36)で、「2n − 1 が素数ならば、2n−1(2n − 1) は完全数である」ということを証明した[注釈 1]。2n − 1 で表される数をメルセンヌ数といい、それが素数である場合をメルセンヌ素数という。
古代から、6、28、496、8128の4つの数が完全数であることは知られており、ゲラサのニコマコスの『算術入門』には4つの完全数に関する記述が存在する[4]。
ユークリッドの公式は2以上の n に対して偶数の完全数しか生成しない(1のときは唯一の1倍完全数である1になる)が、逆に偶数の完全数が全て 2n−1(2n − 1) の形で書けるかどうかは18世紀までは未解決であった。レオンハルト・オイラーは偶数の完全数がこの形に限ることを証明した[5][6][注釈 2]。
メルセンヌ素数の探索は、エドゥアール・リュカとデリック・ヘンリー・レーマーによってメルセンヌ数が素数であるかどうかの効率的な判定法が考案され、1950年代からコンピュータが使われるようになる。現在では分散コンピューティング GIMPS による探求が行われていて、2024年11月現在[update]で判明している最大のメルセンヌ素数は4102万4320桁の数である[8]。
| 偶数の完全数は無数にあるか。また、奇数の完全数は存在するか。 |
2024年11月現在[update]発見されている完全数はメルセンヌ素数と同じく52個である。紀元前より考察されている対象であるにもかかわらず、「偶数の完全数は無数に存在するか?」「奇数の完全数は存在するか?」という問題は未解決である。
Remove ads
概要
完全数は、小さい順に
である。
各完全数の正の約数の総和は
- 12, 56, 992, 16256, 67100672, 17179738112, …(オンライン整数列大辞典の数列 A139256)
隣り合う完全数の差は
- 22, 468, 7632, 33542208, 8556318720, …(オンライン整数列大辞典の数列 A139228)
完全数の総和の列は
である。
6 と 28 がなぜ「完全」であるかは中世の学者の議論の対象になり、6 は神が創造した1週間(日曜日は神が天地創造を終えて休んだ安息日で、キリスト教ではこれを除外する)、28 は「月の公転周期」とされた[1]。聖アウグスティヌス(? - 604年)はこれとは一線を画し、「6 はそれ自体完全な数である。神が万物を6日間で創造したから 6 が完全なのでなく、むしろ逆が真である」としている[1]。
偶数の完全数 2p−1(2p − 1) = (Mp+1)Mp/2 は Mp 番目の三角数であり、Mp+1/2 番目の六角数でもある。
Remove ads
完全数の分類
要約
視点
→「ユークリッド・オイラーの定理」も参照
偶数の完全数
偶数の完全数は、Mp = 2p − 1 が素数のときの 2p−1Mp に限る(ユークリッド、オイラー)。
ユークリッドの証明
2p−1Mp が完全数であることの証明:[9]
オイラーの証明
偶数の完全数は 2p−1Mp の形に限ることの証明[5][6][注釈 2]:
オイラーの証明
N を偶数の完全数とする。N を 2 で割り切る最大回数を n とすると、N = 2nK(n は自然数、K は奇数)とおける。2n と K は互いに素であるので、σ(n) を約数関数とすると、約数関数は乗法的なので、N の正の約数の総和 σ(N) は以下のようになる。
N は完全数であるため、 σ(N) = 2N = 2n+1K なので
が導かれる。2n+1 − 1 は奇数なので 2 で割り切れず、式が成立するためには、σ(K) は 2n+1 で割り切れなければならない。 σ(K) = 2n+1a とおき、上の式に代入して両辺を 2n+1 で割れば
となる。
もし a ≠ 1 なら、1、 a、 (2n+1 − 1)a は K の相異なる約数のため、
となり矛盾する。ゆえに、a = 1 でなければならない。したがって、N が偶数の完全数であるためには、
- かつ
でなければならない。σ(K) = K + 1 より、K は K と 1 以外に約数がない素数でなければならない。
ゆえに、N が偶数の完全数であるのは、 N = 2n(2n+1 − 1)(ただし 2n+1 − 1 は素数)の形のときに限られる。Q.E.D.
偶数の完全数の性質
偶数の完全数を N = 2p−1(2p − 1)(2p −1 は素数)とする。
- N の正の約数の個数は d(N) = 2p である(d は約数の個数を表す約数関数)。このうち半数は 2 の累乗であり、残り半数はこれにメルセンヌ素数を乗じた数である。
- N の正の約数の調和平均は p、ゆえに N は調和数である。
- 6 以外の偶数の完全数は、1 から連続する正の奇数の立方和で表せる。式で表すと
- 例:
- 28 = 13 + 33, 496 = 13 + 33 + 53 + 73, 8128 = 13 + 33 + 53 + 73 + 93 + 113 + 133 + 153
- 1 から連続する正の奇数の立方和で表せる数の列は
- 1, 28, 153, 496, 1225, 2556, 4753, 8128, …(オンライン整数列大辞典の数列 A002593)
- 2n−1(2n − 1)(n は自然数)の列は
- 1, 6, 28, 120, 496, 2016, 8128, 32640, …(オンライン整数列大辞典の数列 A006516)
- この数列で完全数にならない数の数列は オンライン整数列大辞典の数列 A144858 を参照
- n × σ(n) は n = 2p−1 のとき偶数の完全数になる。ただし σ は約数関数である。この数列は
- 1, 6, 12, 28, 30, 72, 56, 120, 117, 180, 132, 336, 182, 336, 360, 496, 306, 702, 380, 840, …(オンライン整数列大辞典の数列 A064987)
- 偶数の完全数は、1 からメルセンヌ素数まで連続する正の整数の和で表せる。式で表すと
- 例:6 = 1 + 2 + 3 , 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7 , 496 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ... + 28 + 29 + 30 + 31
- 言い換えると、N は 2p − 1 番目の三角数である。偶数の三角数の列は
- 6, 10, 28, 36, 66, 78, 120, 136, 190, 210, 276, 300, 378, 406, 496, 528, 630, 666, 780, 820, 946, 990, …(オンライン整数列大辞典の数列 A014494)
- 偶数の完全数は全て奇数番目の三角数でもあるので、知られている完全数は全て六角数でもある。
- 例:6 = 1 + 5 , 28 = 1 + 5 + 9 + 13 , 496 = 1 + 5 + 9 + 13 + ... + 57 + 61
- 言い換えると、N は 2p − 1 番目の六角数である。
六角数の列は
- 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, …(オンライン整数列大辞典の数列 A000384)
- 知られている完全数は全て 4n − 1 番目の三角数でもあるので偶数の六角数であり、偶数番目の六角数である。n 番目の六角数は n(2n − 1) なので、偶数の六角数は 2n(4n − 1) で表される。偶数の六角数の列は
- 6 以外の完全数は中心つき九角数に含まれる。この数の列は
- N を十進法表示したとき、一の位は 6 または 8 である。
偶数の完全数の未解決問題
偶数の完全数は無数に存在するか、つまり Mp = 2p − 1 が素数となる素数 p は無数に存在するかどうかは未解決である。
奇数の完全数
奇数の完全数が存在するか否かは未解決であるが、約数関数は乗法的 (英: multiplicative) であることから、二平方数の和であることが古くから知られていた。もし奇数の完全数 N が存在すれば、N は以下の各条件を満たさなければならないことが知られている。
- N の素因数分解は qαp12e1 … pk2ek の形である。ここで q, p1 < p2 < … < pk は相異なる素数で q ≡ α ≡ 1 (mod 4) を満たす[注釈 3]。
- N < 24k+1 である[11]。
- p1 < 2/3k + 2 である[12]。また 2 ≤ i ≤ 6 のとき pi < 22i−1(k − i + 1) である[13]。
- e1 ≡ e2 ≡ … ≡ ek ≡ 1 (mod 3) ではない[14]。
- e1 ≡ e2 ≡ … ≡ ek ≡ 2 (mod 5) ではない[15].
- e1 = e2 = … = ek = β とすると、β は 1, 2, 3, 5, 6, 8, 11, 12, 14, 17, 18, 24, 62 ではない[16][17]。さらにk ≤ 2β2 + 8β + 2 である[18]。
- N ≡ 1 (mod 12) または N ≡ 1/2 ・ 32e1(32e1+1 − 1) (mod 2 ・ 32e1(32e1+1 − 1)) である[19][20][21][22]。
- N > 101500 である[23]。
- これは1991年に示された[24]を約20年ぶりに改良したものである。
- N は少なくとも10個の相異なる素因数を持つ[25]。
- N が 3 で割り切れない場合は、少なくとも12個の素因数を持つ[26]。3 でも 5 でも割り切れない場合は15個以上の、3 でも 5 でも 7 でも割り切れない場合は27個以上の相異なる素因数を持つ[30]。
- N は重複も数えて少なくとも101個の素因数を持つ[23][31]。
- N は 108 より大きい素因数を持つ[32]。
- N の2番目に大きな素因数は 104 より大きい[35]。
- N の3番目に大きな素因数は 100 より大きい[36]。
- N は 1062 より大きい素数冪因数を持つ[23]。
- 2N(Nの約数の和) は単偶数の3倍完全数となる(未発見。倍積完全数を参照。)。
2006年にカール・ポメランスは、1以外の奇数の調和数が発見されていないという事実から、ヒューリスティクスな議論ではあるが、奇数の完全数は存在しないだろうとする論を発表しているが、予想の域を出ない[37]。
その他の性質
- 完全数は、正の約数の個数が偶数、正の約数の逆数和が 2 なので、調和数である。この数の列は
- 完全数は素数ではないが、約数の和が自分自身(の1倍)に等しい唯一の数である 1 との関係において、2個の約数を持つ素数が1個の約数を持つ唯一の数である 1 に対するのと似た関係を持つ。
Remove ads
関連する数
要約
視点
約数の和や積を考えることで特徴付けられる数の種類には他にも次のようなものがある。完全数と併せて、これらの名称には古代ギリシアの数秘学の影響が見られる。
完全数の拡張
- 倍積完全数 (multiperfect number)[38]
- 正の約数の和が自分自身の倍数である自然数を倍積完全数という。特に、それがk倍に等しいものをk倍完全数という。1は唯一の1倍完全数であり、完全数とは2倍完全数のことである。
- 1, 6, 28, 120, 496, 672, 8128, 30240, …(オンライン整数列大辞典の数列 A007691)
- ハイパー完全数 (hyperperfect number)
- n が k -ハイパー完全数であるとは、
- n = 1 + k(σ(n) − n − 1)(ただしk は自然数)(σ は約数関数)
- を満たすことと定義される。完全数は 1-ハイパー完全数である。
- k -ハイパー完全数の列は
- 6, 21, 28, 301, 325, 496, 697, 1333, 1909, 2041, 2133, 3901, 8128, …(オンライン整数列大辞典の数列 A034897)
- 超完全数 (superperfect number)
- n が (m, k)-完全数であるとは、
- σm(n) = kn(ただし k は自然数)(σ は約数関数)
- を満たすときと定義される。完全数は (1, 2)-完全数、倍積完全数は (1, k)-完全数、超完全数は (2, 2)-完全数である。
- 擬似完全数 (semiperfect number)
- 自分自身を除くいくつかの約数の総和が元の数に等しい自然数を擬似完全数という。
不完全数
完全数でない自然数を不完全数 (imperfect number) という。
- 不足数 (deficient number)[39]
- 自分自身以外の正の約数の和より大きい自然数
- 過剰数 (abundant number)[40]
- 自分自身以外の正の約数の和より小さい自然数。過剰数であって擬似完全数でない数を不思議数という。
- 友愛数 (amicable pair)[41]
- 自分自身以外の正の約数の和が互いに他方に等しい2つの自然数の組。
- 社交数 (sociable numbers)[42]
- 友愛数と同様の関係が成立する3個以上の自然数の組。
- 準完全数 (quasiperfect number)[43]
- n が準完全数であるとは、正の約数の和が 2n + 1 に等しいことと定義される。過剰数の一種。そのような数はいまだに見つかっていないが、存在するならばそれは奇数の平方数で 1035 より大きく、少なくとも7つの約数を持つということが示されている。
- 概完全数 (almost perfect number)[44]
- n が概完全数であるとは、正の約数の和が 2n − 1 に等しいことと定義される。不足数の一種。2k (= 1, 2, 4, 8, 16, …) の形の自然数はこの条件を満たしているが、この形の自然数以外の概完全数が存在するのかどうかは知られていない。
その他
Remove ads
エピソード
小川洋子の小説『博士の愛した数式』(2003年)では登場人物の「博士」が阪神タイガースの江夏豊投手のファンであったことの理由として江夏の背番号が28であったことを挙げ、その際に完全数の説明がなされている。
江夏ではないが、日本のプロ野球で初めて完全試合が達成されたのは月・日とも完全数の1950年6月28日だった。6月28日は「完全」の意味を持つ食べ物「パフェの日」にもなっている。
脚注
参考文献
関連項目
外部リンク
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads













