Аркус тангенс

Аркус тангенс – функција инверзна на тангенсната функција во ограничениот интервал [-π/2,π/2]. Се користи за одредување на големина на агол во овој опсег, када е позната вредноста на неговиот тангенс. Може да се дефинира со следната формула:

${\displaystyle \operatorname {arctg} \;x=\tan ^{-1}x={\frac {i}{2}}\left(\log(1-ix)-\log(ix+1)\right)}$

Аркус тангенс
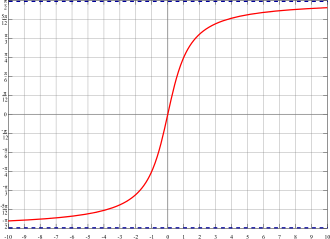y(x)=arctg(x)
Основни особини
Домен	(-∞,∞)
Кодомен	(-π/2,π/2)
Паритет	непарна
Одредени вредности
Асимптота	y = ± π/2
Вредност х=+∞	π/2
Вредност х=-∞	-π/2
Други особини
Извод	:${\displaystyle {\frac {1}{1+x^{2}}}}$
Превојна точка	(0, 0)

Формули

Формули кои се поврзани со аркус тангенс:

${\displaystyle \operatorname {arctg} \;x={\frac {\pi }{2}}-\operatorname {arcctg} \;x}$ (правило на комплементарни агли)

${\displaystyle \operatorname {arctg} (-x)=-\operatorname {arctg} \;x\!}$ (непарност на функцијата)

${\displaystyle \operatorname {arctg} \;{\frac {1}{x}}={\frac {\pi }{2}}-\operatorname {arctg} \;x=\operatorname {arcctg} \;x,\ }$ ${\displaystyle x>0}$

${\displaystyle \operatorname {arctg} \;{\frac {1}{x}}=-{\frac {\pi }{2}}-\operatorname {arctg} \;x=-\pi +\operatorname {arcctg} \;x,\ }$ ${\displaystyle x<0}$

Преку формулата за половина агол се добива и:

${\displaystyle \operatorname {arctg} \;x=2\operatorname {arctg} \;{\frac {x}{1+{\sqrt {1+x^{2}}}}}}$

Извод

Изводот на аркус тангенс е:

${\displaystyle {\frac {d}{dx}}\operatorname {arctg} \;x{}={\frac {1}{1+x^{2}}}}$

Претставување во форма на интеграл

Претставена во форма на интеграл аркус тангенс е:

${\displaystyle \operatorname {arctg} \;x{}=\int _{0}^{x}{\frac {1}{x^{2}+1}}\,dx}$

Претставување во форма на бесконечна сума

Претставена во форма на бесконечна сума аркус тангенс е:

${\displaystyle {\begin{aligned}\operatorname {arctg} x&{}=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{2n+1}};\qquad |x|\leq 1\qquad x\neq i,-i\end{aligned}}}$

Поврзано

• Тригонометриски функции
• Инверзни тригонометриски функции

Надворешни врски

• ArcTan/ Функцијата аркус тангенс на wolfram.com

Тригонометриски и хиперболични функции

Синус Косинус Тангенс Котангенс Секанс Косеканс Функција sin(x) cos(x) tg(x) ctg(x) sec(x) cosec(x) Инверзна arcsin(x) arccos(x) arctg(x) arcctg(x) arcsec(x) arccosec(x) Хиперболична sinh(x) cosh(x) tgh(x) ctgh(x) sech(x) cosech(x) Инв. хиперболична arcsinh(x) arccosh(x) arctgh(x) arcctgh(x) arcsech(x) arccosech(x)