Funkcja τ

Funkcja τ (tau) – funkcja na zbiorze dodatnich liczb naturalnych, używana w teorii liczb. Jej wartość to liczba dzielników danej liczby^[1][2].

Wykres funkcji dla argumentów od 1 do 250

Dla dowolnej liczby ${\displaystyle n\in \mathbb {N} _{+}}$ funkcja ${\displaystyle \tau (n)}$ określona jest jako:

${\displaystyle \tau (n):=|\{d\in \mathbb {N} :d|n\}|.}$

Wzór można też zapisać inaczej:

${\displaystyle \tau (n)\equiv \sigma _{0}(n)=\sum _{d|n}1.}$

Uogólnieniem funkcji tau są funkcje σ (sigma); funkcja tau to funkcja sigma stopnia zerowego^{[potrzebny przypis]}.

Własności

Wiedząc, że funkcja ta jest multiplikatywna^[1] oraz że dla dowolnej liczby pierwszej ${\displaystyle p}$ i dowolnej liczby całkowitej nieujemnej ${\displaystyle a}$ zachodzi^[3]:

${\displaystyle \tau (p^{a})=a+1,}$

(ponieważ dzielnikami liczby ${\displaystyle p^{a}}$ są: ${\displaystyle 1,p,p^{2},\dots ,p^{a}}$) otrzymujemy wzór ogólny dla funkcji ${\displaystyle \tau (n).}$

Niech ${\displaystyle n=\prod _{i=1}^{m}p_{i}^{e_{i}},}$

gdzie:

${\displaystyle m}$ – liczba czynników pierwszych,

${\displaystyle e_{i}}$ – wykładniki w rozkładzie na czynniki pierwsze,

${\displaystyle p_{i}}$ – parami różne czynniki pierwsze.

Wtedy^[2]:

${\displaystyle \tau (n)=\prod _{i=1}^{m}(e_{i}+1).}$

Przykład

Jeśli ${\displaystyle n=24,}$ to mamy dwa dzielniki pierwsze: ${\displaystyle p_{1}=2,p_{2}=3,}$ ponieważ ${\displaystyle 24=2^{3}\cdot 3^{1},}$ czyli ${\displaystyle e_{1}=3,e_{2}=1.}$ Można zatem obliczyć ${\displaystyle \tau (24)}$ w sposób następujący:

${\displaystyle \tau (24)=\prod _{i=1}^{2}(e_{i}+1)=(3+1)(1+1)=4\cdot 2=8.}$

Faktycznie, zbiór dzielników liczby 24 to zbiór ${\displaystyle \{1,2,4,8,3,6,12,24\},}$ którego moc wynosi 8.

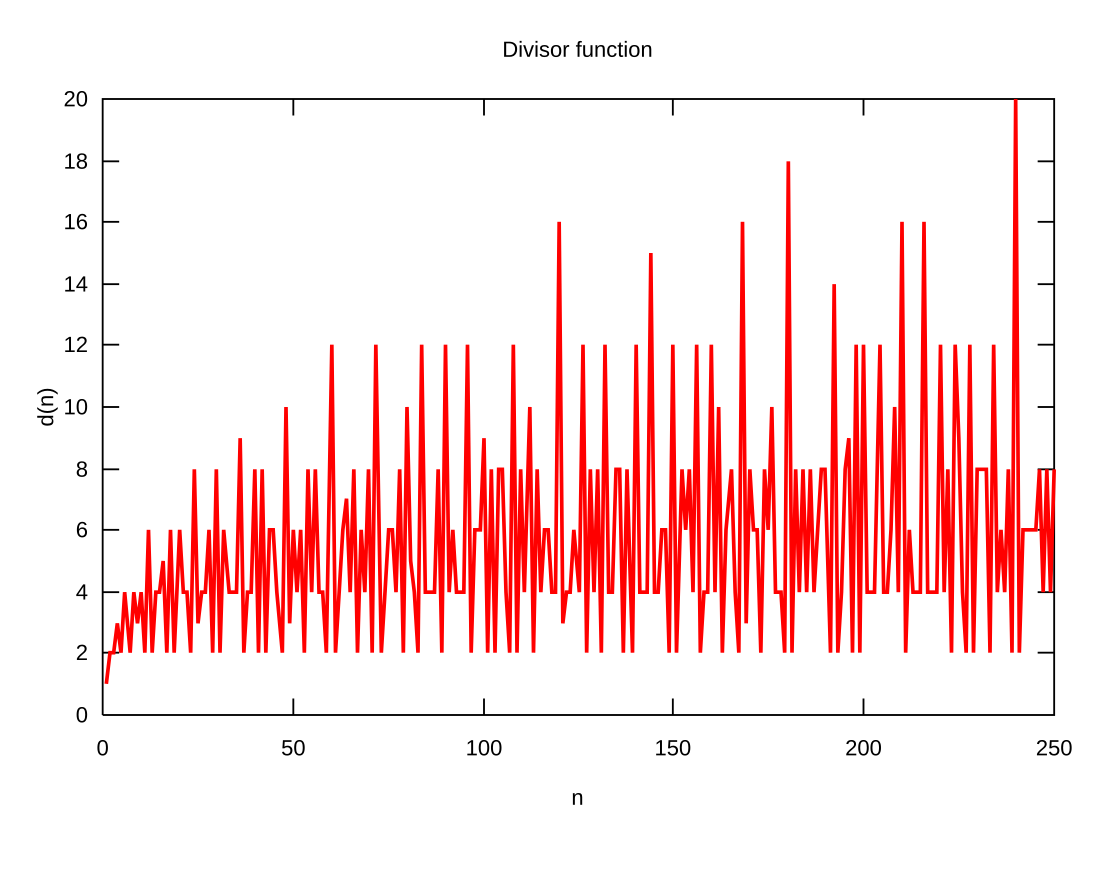
Pierwsze wartości przyjmowane przez funkcję (ciąg A000005 w OEIS) to:

${\displaystyle n}$	1	2	3	4	5	6	7	8	9	10	11	12
Dzielniki liczby ${\displaystyle n}$	1	1, 2	1, 3	1, 2, 4	1, 5	1, 2, 3, 6	1, 7	1, 2, 4, 8	1, 3, 9	1, 2, 5, 10	1, 11	1, 2, 3, 4, 6, 12
${\displaystyle d(n)}$	1	2	2	3	2	4	2	4	3	4	2	6