Funkcja

Funkcja (łac. functio, -onis „odbywanie, wykonywanie, czynność”^[a]), odwzorowanie^[1][2], przekształcenie^[3], transformacja^[4] ze zbioru ${\displaystyle X}$ do zbioru ${\displaystyle Y,}$ która każdemu elementowi zbioru ${\displaystyle X}$ przypisuje (odwzorowuje) dokładnie jeden element zbioru ${\displaystyle Y}$^[5].

Ten artykuł dotyczy pojęcia matematycznego. Zobacz też: inne znaczenia słowa „funkcja”.

Metaforyczne (ale prezycyjne) przedstawienie funkcji ${\displaystyle f}$ jako maszyny, która przekształca dany element ${\displaystyle x}$ ze zbioru ${\displaystyle X}$, na pewien element ${\displaystyle y}$ ze zbioru ${\displaystyle Y}$.

Diagram przedstawiajacy funkcję: każdemu elementowi zbioru ${\displaystyle X}$ przyporządkowano (strzałką) dokładnie jeden element zbioru ${\displaystyle Y}$.

Funkcje stały się jednym z podstawowych i najważniejszych pojęć całej nowożytnej matematyki^[6] i innych nauk ścisłych oraz stosowanych, o szerokich zastosowaniach w działalności człowieka na wielu polach.

Formalna definicja

Funkcja ${\displaystyle f=(X,Y,W)}$ to trójka uporządkowana składająca się z poniższych elementów^{[7][8][9][10][11][12][13]}:

• dziedziny ${\displaystyle X}$ będącej dowolnym zbiorem (którego elementy nazywamy argumentami funkcji^[14]),
• przeciwdziedziny ${\displaystyle Y}$ również będącej dowolnym zbiorem (którego elementy nazywamy wartościami funkcji^[14]),
• wykresu ${\displaystyle W\subseteq X\times Y}$ będącym zbiorem par, takim że ${\displaystyle \forall x\in X,\exists !y\in Y:(x,y)\in W.}$

Wyjaśnienie

Wykres ${\displaystyle W}$ to zbiór tylko takich par, że dla każdego elementu ${\displaystyle x}$ z ${\displaystyle X}$ istnieje dokładnie jeden ${\displaystyle y}$ z ${\displaystyle Y,}$ taki że para ${\displaystyle (x,y)}$ znajduje się w zbiorze ${\displaystyle W}$ (czyli każdemu ${\displaystyle x}$ jest przyporządkowany dokładnie jeden ${\displaystyle y}$ a razem stanowią parę która jest „punktem” z wykresu funkcji).

Zauważmy że dla teoriomnogościowej definicji trójki jako pewnego zbioru (co zwykle się przyjmuje), funkcja ${\displaystyle f}$ staje się zbiorem.

Powyższa definicja nazywana jest definicją Bourbakiego^[7][8] (wprowadzoną w 1954 r.^[15]), a jej odmianą zredukowaną tylko do wykresu (tj. ${\displaystyle f=W}$), również powszechnie używaną jest definicja Peana.

Przykład ${\displaystyle }$

Niech dziedzina będzie zbiorem składającym się z trzech liczb tj. ${\displaystyle X=\{1,2,3\}}$, przedziwdziedzina zbiorem składającym się z czterech liter tj. ${\displaystyle Y=\{a,b,c,d\}}$. Niech wykres funkcji będzie następującym zbiorem ${\displaystyle W=\{(1,a),(2,b),(3,b)\}}$. Wówczas możemy zapisać formalnie funkcję ${\displaystyle f}$ jak następującą trójkę zbiorów: ${\displaystyle f={\Big (}\ \ \ \{1,2,3\},\ \ \ \{a,b,c,d\},\ \ \ \{(1,a),(2,b),(3,b)\}\ \ \ {\Big )}}$ Na obrazku poniżej znajduje się przedstawienie trzech elementów powyższej funkcji czyli zbiorów ${\displaystyle X,Y,W}$. W celach poglądowych, elmenty z ${\displaystyle X}$ i ${\displaystyle Y}$ tworzące pary w zbiorze ${\displaystyle W}$ połączono szarymi strzałkami. Przedstawienie trzech elementów funkcji: dziedziny X, przeciwdziedziny Y oraz wykresu W. W celach poglądowych nasieniono szare strzałki obrazujące pary zawarte w W W świetle formalnej definicji funkcji, zwróćmy uwagę że każdy element z dziedziny ${\displaystyle X}$ musi znajdować się w dokładnie jednej parze (jako jej pierwszy element) w zbiorze ${\displaystyle W}$ tzn. patrząc na obrazek, z kadego elementu należacego do zbioru ${\displaystyle X}$ musi wychodzić dokładnie jedna szara strzałka (do jakiegoś elementu z ${\displaystyle Y}$), jeżeli z jakiegoś elementu w ${\displaystyle X}$ nie wychodziła by żadna strzałka (nie miał by pary) albo wychodziły by dwie strzałki lub więcej (byłby w wielu parach), to ${\displaystyle f}$ nie było by funkcją, nie każdy element z przeciwdziedziny ${\displaystyle Y}$ musi być elementem jakieś pary np. litera ${\displaystyle c}$ nie ma pary, dany element ze zbioru ${\displaystyle Y}$ może być elementem wielu par np. litera ${\displaystyle b}$ występuje w dwóch parach: ${\displaystyle (2,b)}$ oraz ${\displaystyle (3,b)}$, wykres czyli zbiór ${\displaystyle W}$ nie może zawierać par w których pierwszy element pary nie należy do ${\displaystyle X}$ lub drugi element pary nie należy do ${\displaystyle Y}$ np. dla powyższej funkcji to takie pary w zbiorze ${\displaystyle W}$ są niedozwolone: ${\displaystyle (a,1)}$, ${\displaystyle (4,b)}$, ${\displaystyle (1,e)}$ czy ${\displaystyle (5,g)}$ . Korzystając z notacji tradycyjnej (zwykle używanej) funkcję ${\displaystyle f}$ zapisalibyśmy następująco: ${\displaystyle f:\{1,2,3\}\rightarrow \{a,b,c,d\},f(x)={\begin{cases}a,&{\text{gdy }}x=1\\b,&{\text{gdy }}x=2{\text{ lub }}x=3.\\\end{cases}}}$

Notacja

Funkcje oznacza się na ogół literami (małymi lub dużymi) ${\displaystyle f,g,h}$ itd., ale stosuje się również litery greckie np. funkcja dzeta ${\displaystyle \zeta }$, oznaczenia wieloliterowe np. sin, czy symbole np. iloczyn wektorowy ${\displaystyle \times }$. Dziedzinę i przeciwdziedzinę funkcji ${\displaystyle f}$ przyporządkowującej elementom zbioru ${\displaystyle X}$ elementy zbioru ${\displaystyle Y}$, tradycyjnie zapisuje się w poniższy sposób:

${\displaystyle f\colon X\to Y}$.

Wartość ${\displaystyle y}$ funkcji ${\displaystyle f}$ dla argumentu ${\displaystyle x}$ zapisujemy zwykle w formie formuły ${\displaystyle f(x)=y}$, która jednocześnie definije caly wykres funkcji ${\displaystyle f}$. Ale stosuje się również indywidualne notacje dla niektórych funkcji np. wartość bezwzględna ${\displaystyle |x|}$, silnia ${\displaystyle n!}$, dodawanie ${\displaystyle +}$ (i inne działania), i tym podobne.

Pełny tradycyjny zapis funkcji (zawierający informację o dziedzinie, przeciwdziedzinie i wykresie) jest zgodny z szablonem:

${\displaystyle f\colon X\to Y}$, ${\displaystyle f(x)=y}$

Przykład ${\displaystyle }$

Dana jest funkcja ${\displaystyle f\colon \mathbb {N} \to \mathbb {R} }$ określona wzorem ${\displaystyle f(x)=x/2}$, tu najpierw podano dziedzinę ${\displaystyle \mathbb {N} }$ (liczby naturane) i przeciwdziedzinę ${\displaystyle \mathbb {R} }$ (liczby rzeczywiste), a następnie osobno zdefiniowano wykres (zbiór ${\displaystyle W}$ w formalnej definicji) poprzez formułę pozwalającą wyznaczyć każdy jego element - czyli każdą parę ${\displaystyle (x,y)=(x,f(x))=(x,x/2)}$, gdzie ${\displaystyle x\in \mathbb {N} }$, oraz ${\displaystyle y\in \mathbb {R} }$ (symbol ${\displaystyle \in }$ oznacza przynależność do zbioru). Dokładniej: poprzez podstawienie danego elementu ${\displaystyle x}$ dziedziny pod formułę ${\displaystyle f(x)=x/2=y}$ otrzymamy element przeciwdziedziny ${\displaystyle y}$, co pozwoli skonstruować parę ${\displaystyle (x,y)}$ bądącą elementem (punktem) wykresu ${\displaystyle W}$ funkcji, np. dla ${\displaystyle x=6}$ podstawiamy ${\displaystyle f(6)=6/2=3}$ - otrzymaliśmy więc parę ${\displaystyle (6,3)\in W}$, jeśli podobnie ucznimy dla pozostalych elementów dziedziny to znajdziemy wszystkie punktu (elementy) wykresu. Bardziej formalny zapis (którego zwykle się nie stosuje w praktyce) dla tego przykładu wyglądałby tak: ${\displaystyle f=\left(\mathbb {N} ,\mathbb {R} ,\left\{\left(x,{\frac {x}{2}}\right):x\in \mathbb {N} \right\}\right).}$ Jeżeli pomija się podanie dziedziny i przeciwdziedziny dla danej funkcji to oznacza, że należy wywieść te informacje z wykresu lub kontekstu – co często ma miejsce (i uzasadnia oddzielenie definicji wykresu w tradycyjnej notacji).

Zmienna zależna i niezalezna

Zapiszmy wykres funkcji w formie formuły ${\displaystyle f(x)=y}$. Zmienną ${\displaystyle x}$, oznaczającą dowolny argument funkcji, nazywamy zmienną niezależną. Zmienną ${\displaystyle y}$ nazywamy zmienną zależną gdyż jej konkretna wartość zależy od ${\displaystyle f}$ i wybranego ${\displaystyle x}$^[16].

Zbiór wszystkich funkcji

Zbiór wszystkich funkcji ze zbioru ${\displaystyle X}$ do zbioru ${\displaystyle Y}$ oznacza się ${\displaystyle Y^{X}}$^[2].

Notacja dla funkcji wielu zmiennych

Zgodnie z definicja formalną, każda funkcja może przyjmować dokładnie jeden argument (który jest elementem dziedziny). Jednak dziedzina w szczególności może być zbiorem par albo trójek albo w ogólności n-tek . Funkcje o takiej dziedzinie nazywamy funkcjami wielu zmiennych. Do ich zapisu stosuje się skrót notacyjny polegający na omijaniu nawiasów funkcji, podczas podstawiania do niej danej pary/trójki/n-tki . Przykładowo dla funkcji która dla danego punktu płaszczyzny euklidesowej wyznacza jego wysokość tj. ${\displaystyle f:\mathbb {R} ^{2}\rightarrow \mathbb {R} }$, gdy postawimy punkt ${\displaystyle (1,2)}$, czyli argument który jest parą liczb, to zamiast pisać

${\displaystyle f((1,2))}$

zapisujemy skrótowo:

${\displaystyle f(1,2)}$

Warto wspomanieć, że wynikiem funkcji również jest dokładnie jedna wartość ale może ona być n-tką zawierająca wiele elementów (np. ${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{3}}$ przyjmuje parę a zwraca trójkę liczb).

Szczegółowe przykłady ${\displaystyle }$

Rozważmy funkcję której dziedzina to ${\displaystyle \mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R} =\left\{(u,v)\colon u\in \mathbb {R} \;\wedge \;v\in \mathbb {R} \right\}}$ (iloczyn kartezjański) czyli każdy element ${\displaystyle x\in \mathbb {R} ^{2}}$ z dziedziny jest parą dwóch liczb rzeczywistych tj. ${\displaystyle x=(u,v)}$. Przeciwdziedziną zaś niech będzie ${\displaystyle \mathbb {R} }$ zaś wykresem ${\displaystyle f(x)=f((u,v))=u^{2}+v^{2}}$. Zwróćmy uwagę że tak zdefiniowana funkcja przyjmuje defacto dwie liczby ${\displaystyle u,v}$ (stanowiące jedną parę ${\displaystyle (u,v)}$ oznaczoną przez ${\displaystyle x}$ ) jako argument a zwraca w wyniku jedną liczbę (będącą sumą kwadratów elementów pary). Kożystając z tradycyjnej notacji zapiszemy ${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} }$, ${\displaystyle f(u,v)=u^{2}+v^{2}}$ zwróćmy uwagę, że zamiast ${\displaystyle f((u,v))}$ zapisano ${\displaystyle f(u,v)}$ a więc pominięto wewnętrzne nawiasy - jest to powszechnie stosowany skrót notacyjny. Formalnie funkcja przyjmuje tylko jeden argument (który jest parą liczb). Formalnie powyższa funkcja ma taką postać: ${\displaystyle f=\left(\mathbb {R} ^{2},\mathbb {R} ,\left\{\left((u,v),u^{2}+v^{2}\right):u,v\in \mathbb {R} \right\}\right)}$ ${\displaystyle f:[0,1]^{4}\to \mathbb {R} ,f(x,y,z,t)=t+xyz}$, (${\displaystyle [0,1]}$ to przedział domknięty wszystkich liczb rzeczywistych od 0 do 1) z definicji ${\displaystyle f=([0,1]^{4},\mathbb {\mathbb {R} } ,\{((x,y,z,t),t+xyz):x,y,z,t\in [0,1]\})}$, np. funkcja określa temperaturęw każdym punkcie kostki o boku 1, w każdym momencie przedział czasu od 0 do 1. ${\displaystyle f:\mathbb {R} \to \mathbb {\mathbb {R} } ^{3},f(x)=(x^{2},x,0)}$. Wynikiem działania tej funkcji jest trójka liczb którą można interpretować jak współrzedne x,y,z w przestrzeni 3D (w tym przypadku z=0). Z definicji ${\displaystyle f=(\mathbb {R} ,\mathbb {R} ^{3},\{(x,(x^{2},x,0)):x\in \mathbb {R} \})}$ (funkcja przyporządkowuje każdej liczbie pewien punkt na płaszczyźnie (z=0) w przestrzeni trójwymiarowej - czyli rysuje płaską krzywą w 3D), np. funkcja określa położenie pewnego pojazdu na płaskiej nawierzchni w czasie x.

Indywidualna notacja/nazewnictwo dla wybranych funkcji: działań, funkcjonałów, operatorów

Jak wspomniano powyżej, stosuje się indywitualną notacje dla niektórych funkcji jednej zmiennej np. wartość bezwzględna ${\displaystyle |x|}$, silnia ${\displaystyle n!}$, Potęgowanie ${\displaystyle x^{a}}$ itp.

Operacje arytmetyczne są kolejnym przykłądem funkcji dla których stosuje się indywidualną notację np. dodawanie liczb naturalnych ${\displaystyle +:\mathbb {N} ^{2}\to \mathbb {N} }$ (do oznaczenia tej funkcji użyto tu znaku "${\displaystyle +}$" zamist litery "${\displaystyle f}$") z indywidualną notacją w której zamiast pisać ${\displaystyle +(a,b)}$ piszemy ${\displaystyle a+b}$, oraz uwzględniamy szereg specyficznych reguł związanych ze składaniem operacji dodawania z samą sobą i innymi operacjami z uwzględnieniem nawiasów. Przykładowo:

${\displaystyle a+b+c=+(+(a,b),c)}$

${\displaystyle (a+b)\cdot c=\cdot (+(a,b),c)}$,

notacja (lewa strona powyższych równości) jest intepretowana (prawa strona równości) jako odpowiednie złożenie funkcji ${\displaystyle +}$ oraz ${\displaystyle \cdot }$ właśnie ze względu na uwzględnienie owych reguł.

Funkcjonał to funkcja która przyjmuje inną funkcję jako argument i zwraca liczbę jako wynik. Niektóre funkcjonały posiadają indywidualną notację np. funkcjonał ${\displaystyle F:C\to \mathbb {\mathbb {R} } }$ (gdzie ${\displaystyle C\subset \mathbb {R} ^{R}}$ tu zbiór wszystkich funkcji rzeczywistych całkowalnych w sensie Riemana na przedziale ${\displaystyle [a,b]}$) zwracający pole pod wykresem funkcji na przedziale ${\displaystyle [a,b]}$ dla danej funkcji ${\displaystyle f}$, to zamiast pisać ${\displaystyle F(f)=y}$ piszemy

${\displaystyle \int \limits _{a}^{b}f(x)dx=y}$.

Przykład funkcjonału

${\displaystyle f:\mathbb {N} ^{\mathbb {Z} }\to \mathbb {\mathbb {R} } ,f(x)={\sqrt {x(-1)}}}$, gdzie ${\displaystyle \mathbb {Z} ^{\mathbb {N} }}$ to zbiór wszystkich funkcji ${\displaystyle x:\mathbb {Z} \to \mathbb {N} }$ tj. działających z liczb całkowitych ${\displaystyle \mathbb {Z} }$ w liczby naturalne ${\displaystyle \mathbb {N} }$. Tutaj ${\displaystyle x}$ nie oznacza liczby tylko funkcję, a ${\displaystyle x(-1)}$ to wartość tej funkcji dla minus jedynki. Funkcja ${\displaystyle f(x)}$ zwraca więc pierwiastek z pewnej liczby naturalnej która jest wartością funkcji ${\displaystyle x}$ w minus jeden. Z definicji formalnej zapisujemy ${\displaystyle f=(\mathbb {N} ^{\mathbb {Z} },\mathbb {\mathbb {R} } ,\{(x,{\sqrt {x(-1)}}):x\in \mathbb {Z} ^{\mathbb {N} }\})}$. Funkcja której argumentem są inne funkcje a wartościami liczby (zamienia/mapuje/transformuje funkcje na liczby) to funkcjonał.

Operator to funkcja która jako argument przyjmuje pewną funkcję i zwraca inną funkcję. Operatory transformują/zmieniają daną funkcję na inną i często do ich zapisu stosuje się indywidualna odrębną notację (np. transformata Fouriera ${\displaystyle {\hat {f}}}$, operator składania funkcji ${\displaystyle f\circ g}$, operator Nabla dla gradientu ${\displaystyle \nabla f}$ itp.)

Szczegółowe omówienie wybranych przykładów w świetle formalnej definicji

${\displaystyle f:\mathbb {Z} ^{\mathbb {N} }\to \mathbb {\mathbb {R} } ^{\mathbb {N} },f(x)=\pi x^{2}}$, tutaj funkcja f jako argument bierze pewną funkcję ${\displaystyle x:\mathbb {N} \to \mathbb {Z} }$ a jako wynik zwraca inną funkcję ${\displaystyle y:\mathbb {N} \to \mathbb {R} }$. Funkcje których argumentami są pewne funkcje a wynikiem inne funkcje (czyli zamieniają/transofmują jedne funkcje na inne funkcje) nazywamy operatorami. Poszczególne operatory mogą posiadać indywidualną niezależną notację (i nierzadko nazewnictwo oraz być centralnym elementem teorii matematycznych) np. dywergencja ${\displaystyle div(.),\nabla \cdot }$, transformata Fouriera ${\displaystyle {\hat {f}}}$ etc. Szczegóły przykładu ${\displaystyle }$ Wartość funkcji ${\displaystyle y}$, z przykładu, w każdym punkcie równa jest kwadratowi wartości funkcji ${\displaystyle x}$ w owym punkcie wymnożonym przez ${\displaystyle \pi }$ tj. ${\displaystyle y(t)=\pi (x(t))^{2},t\in \mathbb {N} }$. Z definicji formalnej mamy: ${\displaystyle f=(\mathbb {Z} ^{\mathbb {N} },\mathbb {R} ^{\mathbb {N} },\{(x,\pi x^{2}):x\in \mathbb {Z} ^{\mathbb {N} }\})}$. Ponieważ funkcja ${\displaystyle x}$ ma taką samą dziedzinę jak funkcja ${\displaystyle y}$ oraz ${\displaystyle t}$ w formule na y jest użyte tylko w ${\displaystyle x(t)}$ to możemy operować na nich podobnie jak na zmiennych liczbowych (np. pisząc skrótowo ${\displaystyle y=\pi x^{2}}$ zamiast ${\displaystyle y(t)=\pi x(t)^{2}}$ co skraca notację). ${\displaystyle f:\mathbb {N} ^{\mathbb {Z} }\to \mathbb {\mathbb {R} } ^{\mathbb {Q} },f(x)=y,y(t)=\pi t+2x(\lfloor t\rfloor ),t\in \mathbb {Q} }$ (gdzie ${\displaystyle \lfloor t\rfloor }$ oznacza podłogę, ${\displaystyle \mathbb {Q} }$ to liczby wymierne) funkcja (operator) ${\displaystyle f}$ zmienia funkcję ${\displaystyle x:\mathbb {Z} \to \mathbb {N} }$ w funkcję ${\displaystyle y:\mathbb {Q} \to \mathbb {R} }$. Bardziej formalnie (z definicji) ${\displaystyle f=(\mathbb {N} ^{\mathbb {Z} },\mathbb {\mathbb {R} } ^{\mathbb {Q} },\{(x,(\mathbb {Q} ,\mathbb {R} ,\{(t,\pi t+2x(\lfloor t\rfloor )):t\in \mathbb {Q} \})):x\in \mathbb {N} ^{\mathbb {Z} }\})}$. Przykładowe użycie operatora ${\displaystyle f}$ dla funkcji ${\displaystyle x(s)=3s^{2}+5,s\in \mathbb {Z} }$ czyli zapis ${\displaystyle f(x)=y}$ da w wyniku funkcję ${\displaystyle y(t)=\pi t+2(3\lfloor t\rfloor ^{2}+5)=\pi t+6\lfloor t\rfloor ^{2}+10}$. ${\displaystyle \circ :Z^{Y}\times Y^{X}\to Z^{X},\circ (f,g)(x)=f(g(x))}$ ta funkcja jest operatorem składania dwóch funkcji ${\displaystyle f:Y\to Z}$ oraz ${\displaystyle g:X\to Y}$ który jako wnik zwraca funkcję ${\displaystyle h:X\to Z,h(x)=f(g(x))}$. Dla tego operatora stosuje się notację taką jak dla działań arytmetycznych tj. ${\displaystyle f\circ g}$. Formalnie ${\displaystyle \circ =(Z^{Y}\times Y^{X},Z^{X},\{((f,g),h):f\in Z^{Y},g\in Y^{X},h\in Z^{X},h(x)=f(g(x)),x\in X\})}$

Funkcje róznowartościowe i "na"

Opisano dziesiątki odmian funkcji; niezależnie od dziedziny i przeciwdziedziny można wyróżnić funkcje różnowartościowe (iniekcje), funkcje „na” (suriekcje) oraz przecięcie tych dwóch zbiorów – funkcje wzajemnie jednoznaczne (bijekcje). Inne typy definiuje się m.in. za pomocą konkretnej dziedziny lub przeciwdziedziny, co opisano w dalszych sekcjach.

Funkcje używające tej samej formuły ${\displaystyle f(x)}$ do zdefiniowania wykresu nie muszą być tożsame. Rozważmy taki przypadek czterech funkcji korzystających z formuły ${\displaystyle f(x)=x^{2}}$ (poniżej oznaczono: ${\displaystyle \mathbb {R} }$ to liczby rzeczywiste a ${\displaystyle \mathbb {R} ^{+}}$ to liczby rzeczywiste większe od zera):

${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ^{+},f(x)=x^{2},}$ więc z definicji: ${\displaystyle f=(\mathbb {R} ,\mathbb {R} ^{+},\{(x,x^{2}):x\in \mathbb {R} \}),}$

${\displaystyle g\colon \mathbb {R} \to \mathbb {R} \ ,g(x)=x^{2},}$ więc z definicji: ${\displaystyle g=(\mathbb {R} ,\mathbb {R} ,\{(x,x^{2}):x\in \mathbb {R} \}),}$

${\displaystyle h\colon \mathbb {R} ^{+}\to \mathbb {R} ^{+},h(x)=x^{2},}$ więc z definicji: ${\displaystyle h=(\mathbb {R} ^{+},\mathbb {R} ^{+},\{(x,x^{2}):x\in \mathbb {R} ^{+}\}),}$

${\displaystyle k\colon \mathbb {R} ^{+}\to \mathbb {R} \ ,k(x)=x^{2},}$ więc z definicji: ${\displaystyle k=(\mathbb {R} ^{+},\mathbb {R} ,\{(x,x^{2}):x\in \mathbb {R} ^{+}\}).}$

mamy: ${\displaystyle k\neq g\neq f\neq h\neq k\neq f\neq h\neq g}$ (bo każda jest inną trójką). Każda z funkcji ma inny charakter: ${\displaystyle f}$ to suriekcja, ${\displaystyle h}$ to bijekcja, k to iniekcja.

Obraz i przeciwobraz

• Zbiór ${\displaystyle f(A)=\{y=f(x)\colon x\in A\}}$ jest obrazem podzbioru ${\displaystyle A}$ zbioru ${\displaystyle X}$ w przekształceniu ${\displaystyle f}$^[17],
• dla każdego elementu ${\displaystyle b\in f(X)}$ przeciwobrazem elementu ${\displaystyle b}$ (dokładniej pełnym przeciwobrazem) nazywamy zbiór ${\displaystyle f^{-1}(b)=\{a\in X\colon f(a)=b\};}$ jeśli ${\displaystyle b\notin f(X),}$ to ${\displaystyle f^{-1}(b)=\varnothing }$^[17],
• przeciwobrazem podzbioru ${\displaystyle B\subset Y}$ nazywamy zbiór ${\displaystyle f^{-1}(B)=\{a\in X\colon f(a)\in B\};}$ jeżeli ${\displaystyle B\cap f(X)=\varnothing ,}$ to ${\displaystyle f^{-1}(B)=\varnothing }$^[18].

Wykres funkcji

Osobny artykuł: wykres funkcji.

Wykresem funkcji ${\displaystyle f\colon X\to Y}$ nazywa się zbiór ${\displaystyle W_{f}=\{(x,y)\in X\times Y:y=f(x)\}.}$ Z definicji funkcji wynika, że dla każdego ${\displaystyle x_{0}\in X}$ istnieje dokładnie jeden taki ${\displaystyle y_{0}\in Y,}$ że ${\displaystyle (x_{0},y_{0})\in W_{f}.}$ Jeśli ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ jest funkcją ciągłą, to jej wykres jest krzywą w układzie współrzędnych na płaszczyźnie.

Jeżeli zakładamy, że funkcja jest suriekcją, to wykres funkcji jednoznacznie ją określa. Jeśli ${\displaystyle (x_{0},y_{0})\in W_{f},}$ to ${\displaystyle y_{0}=f(x_{0}),}$ przy czym ${\displaystyle y_{0}}$ jest jedynym takim elementem.

Ogólne przypadki funkcji i nie-funkcji

Poniżej kilka nietypowych/granicznych przypadków – kolumna po stronie lewej trójka f; w środku to interpretacja f jako funkcji w świetle formalnej definicji zapisana w tradycyjnej notacji; ostatnia kolumna to wyjaśnienie (dziedzina ${\displaystyle X}$ i przeciwdziedzina ${\displaystyle Y}$ to dowolne nie puste zbiory, ${\displaystyle W}$ to niepusty wykres dla ${\displaystyle X}$ i ${\displaystyle Y}$)

trójka	tradycyjna notacja	wyjaśnienie
${\displaystyle f=(\emptyset ,\emptyset ,\emptyset )}$	${\displaystyle f\colon \emptyset \to \emptyset ,}$ pusty wykres	dzedzina, przeciwdziedzina i wykres są zbiorami pustymi
${\displaystyle f=(X,\emptyset ,\emptyset )}$	to nie funkcja	jeżeli dziedzina jest niepusta, to i wykres nie może być pusty (skoro dziedzina jest niepusta więc istnieje ${\displaystyle x\in X}$ a więc zgodnie z definicją w ${\displaystyle W}$ musi istnieć para zawierająca ${\displaystyle x}$, zatem ${\displaystyle W\neq \emptyset }$)
${\displaystyle f=(\emptyset ,Y,\emptyset )}$	${\displaystyle f\colon \emptyset \to Y,}$ pusty wykres	dziedzina i wykres są zbiorami pustymi
${\displaystyle f=(\emptyset ,\emptyset ,W)}$	to nie funkcja	jeżeli wykres jest niepusty, to i dziedzina nie może być pusta (skoro ${\displaystyle W\neq \emptyset }$ więc istnieje jakaś para ${\displaystyle (x,y)\in W}$ gdzie ${\displaystyle x\in X}$, zatem ${\displaystyle X\neq \emptyset }$)
${\displaystyle f=(\emptyset ,Y,W)}$	to nie funkcja	jeżeli wykres jest niepusty, to i dziedzina nie może być pusta
${\displaystyle f=(X,\emptyset ,W)}$	to nie funkcja	przeciwdziedzina nie może być zbiorem pustym, bo z definicji funkcji wynika, że dla każdego elementu niepustej dziedziny X musi istnieć dokładnie jeden element przeciwdziedziny.
${\displaystyle f=(X,Y,\emptyset )}$	to nie funkcja	jeżeli dziedzina jest niepusta, to i wykres nie może być pusty
${\displaystyle f=(X,X,W)}$	${\displaystyle f\colon X\to X,f(x)=y,y\in X}$	dziedzina jest równa przeciwdziedzinie
${\displaystyle f=(X,Y,X)}$	to nie funkcja (przy założeniu ZF)	wykres musiałby być tym samym co dziedzina ${\displaystyle W=X}$ (co jest niemożliwe jeśli przyjmujemy aksjomatykę ZF, co zwykle ma miejsce)
${\displaystyle f=(X,Y,Y)}$	to nie funkcja (przy założeniu ZF)	wykres musiałby być tym samym co przeciwdziedzina ${\displaystyle W=Y}$ (co jest niemożliwe jeśli przyjmujemy aksjomatykę ZF, co zwykle ma miejsce)

Funkcje liczbowe

Ważną klasą funkcji są funkcje

${\displaystyle f\colon X\to \mathbb {C} }$ (zbiór ${\displaystyle \mathbb {C} }$ jest zbiorem liczb zespolonych)

nazywane funkcjami o wartościach liczbowych^[19].

W zbiorze funkcji liczbowych określonych na ustalonym zbiorze ${\displaystyle X}$ można zdefiniować działania arytmetyczne:

• Dla ${\displaystyle f,g\colon X\to Y}$ funkcja ${\displaystyle f+g}$ przyjmuje dla każdego ${\displaystyle x\in X}$ wartość ${\displaystyle f(x)+g(x).}$
• Dla ${\displaystyle f,g\colon X\to Y}$ funkcja ${\displaystyle f-g}$ przyjmuje dla każdego ${\displaystyle x\in X}$ wartość ${\displaystyle f(x)-g(x).}$
• Dla ${\displaystyle f,g\colon X\to Y}$ funkcja ${\displaystyle f\cdot g}$ przyjmuje dla każdego ${\displaystyle x\in X}$ wartość ${\displaystyle f(x)\cdot g(x).}$
• Dla ${\displaystyle f,g\colon X\to Y}$ i ${\displaystyle \forall _{x\in X}g(x)\neq 0}$ funkcja ${\displaystyle f/g}$ przyjmuje dla każdego ${\displaystyle x\in X}$ wartość ${\displaystyle f(x)/g(x).}$
• Dla ${\displaystyle f\colon X\to Y}$ i ${\displaystyle \lambda \in \mathbb {C} }$ funkcja ${\displaystyle \lambda \cdot f}$ przyjmuje dla każdego ${\displaystyle x\in X}$ wartość ${\displaystyle \lambda \cdot f(x).}$

Funkcja ${\displaystyle f}$ jest ograniczona, jeśli istnieje taka liczba rzeczywista dodatnia ${\displaystyle M,}$ że dla każdego ${\displaystyle x\in X}$ spełniona jest nierówność ${\displaystyle |f(x)|<M.}$

Jeśli funkcja liczbowa ${\displaystyle f}$ przyjmuje jedynie wartości rzeczywiste

${\displaystyle f\colon X\to \mathbb {R} ,}$

to nazywa się ją funkcją o wartościach rzeczywistych^[19].

Dla funkcji o wartościach rzeczywistych wyniki powyżej zdefiniowanych czterech działań arytmetycznych są funkcjami o wartościach rzeczywistych. Wyjątkiem jest mnożenie przez stałą, która powinna być rzeczywista, aby w wyniku mnożenia funkcji o wartościach rzeczywistych przez tę stałą uzyskać funkcję o wartościach rzeczywistych.

Funkcjami liczbowymi nazywamy:

${\displaystyle f\colon X\to \mathbb {C} ,}$ gdzie ${\displaystyle X\subset \mathbb {C} }$ (jest to funkcja zespolona)

${\displaystyle f\colon X\to \mathbb {R} ,}$ gdzie ${\displaystyle X\subset \mathbb {R} }$ (jest to funkcja rzeczywista)^[20]

Można także mówić o funkcjach liczbowych wielu zmiennych (rzeczywistych lub zespolonych):

${\displaystyle f\colon X\to \mathbb {C} ,}$ gdzie ${\displaystyle X\subset \mathbb {C} ^{n}=\underbrace {\mathbb {C} \times \ldots \times \mathbb {C} } _{n},}$

${\displaystyle f\colon X\to \mathbb {R} ,}$ gdzie ${\displaystyle X\subset \mathbb {R} ^{n}=\underbrace {\mathbb {R} \times \ldots \times \mathbb {R} } _{n},}$

których dziedzina jest podzbiorem iloczynu kartezjańskiego zbioru liczb rzeczywistych lub zbioru liczb zespolonych, które zapisuje się:

${\displaystyle y=f(x_{1},x_{2},\dots ,x_{n}),}$ gdzie ${\displaystyle x_{1},\dots ,x_{n}}$ są współrzędnymi punktu w ${\displaystyle \mathbb {R} ^{n}}$ lub odpowiednio w ${\displaystyle \mathbb {C} ^{n}.}$

Rodzaje funkcji liczbowych

Zobacz też: funkcje elementarne, funkcje specjalne, przebieg zmienności funkcji i granica funkcji.

• funkcja rosnąca;
• funkcja malejąca;
• funkcja nierosnąca;
• funkcja niemalejąca;
• funkcja monotoniczna – funkcja rosnąca lub funkcja malejąca, lub funkcja nierosnąca, lub funkcja niemalejąca;
• funkcje ograniczone – funkcja, której zbiór wartości jest ograniczony;
• funkcja parzysta – wykres funkcji parzystej jest symetryczny względem osi rzędnych;
• funkcja nieparzysta – wykres funkcji nieparzystej jest symetryczny względem początku układu współrzędnych;
• funkcja okresowa;
• funkcja ciągła;
• funkcja różniczkowalna – funkcja, dla której istnieje pochodna w każdym punkcie jej dziedziny.

Przykładem funkcji jest kwadrat liczby: y=x². Funkcja rzeczywista zdefiniowana tym wzorem ma wykres w kartezjańskim układzie współrzędnych – jest nim parabola.

Wykres części rzeczywistej funkcji wykładniczej w dziedzinie zespolonej.

Sposoby określania funkcji

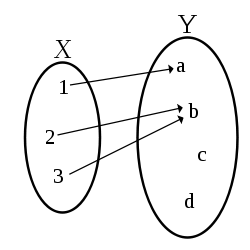
Jeżeli dziedzina ${\displaystyle X}$ jest skończona, wystarczy wymienić wszystkie pary (argument, wartość). Można to zrobić za pomocą grafu (przykład obok).

Funkcje liczbowe można definiować za pomocą wzorów. Jest to sposób analityczny. W tym celu wykorzystuje się pewien zasób funkcji (wielomiany, funkcje elementarne itp.), działania algebraiczne, złożenie funkcji i operację przejścia do granicy (w tym operacje analizy matematycznej, takie jak różniczkowanie, całkowanie i sumowanie szeregów)^[20].

Klasa funkcji, które można przedstawić za pomocą szeregu (potęgowego, trygonometrycznego itp.) jest bardzo szeroka. Każdą funkcję elementarną można przedstawić za pomocą szeregu potęgowego zwanego szeregiem Taylora.

Przedstawić analitycznie funkcję można w sposób jawny, tzn. Jako ${\displaystyle y=f(x)}$ lub jako tak zwaną funkcję uwikłaną, tzn. za pomocą równania ${\displaystyle F(x,y)=0}$^[20].

Czasem funkcja jest dana kilkoma wzorami, na przykład:

${\displaystyle f(x)={\begin{cases}3^{x},&{\text{gdy }}x>0\\0,&{\text{gdy }}x=0\\2x-1&{\text{gdy }}x<0\end{cases}}.}$

Do określenia funkcji można też stosować metodę opisową. Na przykład funkcja Dirichleta jest funkcją, która dla argumentów wymiernych przyjmuje wartość 1, a dla argumentów niewymiernych 0.

Funkcja może na ogół być określona na wiele sposobów. Na przykład funkcję sgn (x) można określić w taki sposób:

${\displaystyle \operatorname {sgn}(x)={\begin{cases}1,&{\text{gdy }}x>0\\0,&{\text{gdy }}x=0\\-1&{\text{gdy }}x<0\end{cases}},}$

albo w taki:

${\displaystyle \operatorname {sgn}(x)={\begin{cases}{\frac {x}{|x|}},&{\text{gdy }}x\neq 0\\0,&{\text{gdy }}x=0\end{cases}}.}$

Dla funkcji rzeczywistych o wartościach rzeczywistych stosowano tabelaryczny sposób określania funkcji. Obecnie w dobie kalkulatorów i arkuszy kalkulacyjnych tabele wartości funkcji logarytmicznych i trygonometrycznych i innych nie są już niezbędne, ale bywają wykorzystywane^[21].

Ważnym sposobem przedstawiania i badania funkcji jest jej wykres, który dla funkcji ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ w przypadku funkcji ciągłej jest krzywą na płaszczyźnie^[21].

Przykłady funkcji liczbowych określonych za pomocą wzoru

• ${\displaystyle y=ax+b}$ – funkcja liniowa
• ${\displaystyle y=ax^{2}+bx+c}$ – funkcja kwadratowa
• ${\displaystyle y=a_{0}+a_{1}x+\ldots +a_{n}x^{n}}$ – funkcja wielomianowa
• ${\displaystyle y=1+{\sqrt {\ln {\sin {2\pi x}}}}}$
• ${\displaystyle P_{n}(x)={\frac {1}{2^{n}n!}}{\frac {d^{n}(x^{2}-1)^{n}}{dx^{n}}}}$
• ${\displaystyle I(\alpha ,\beta )=\int _{0}^{+\infty }e^{-\alpha x}{\frac {\sin \beta x}{x}}dx}$
• ${\displaystyle \sigma (z)=\textstyle \sum _{n=1}^{\infty }{\frac {1}{n^{z}}}}$
• ${\displaystyle y-f(x)=0}$ – funkcja jawna zapisana jako uwikłana
• ${\displaystyle x^{2}+y^{2}-1=0}$ – funkcja uwikłana (równanie okręgu)

Funkcja jako związek między zmiennymi

Zamiast mówić o funkcji jako o relacji między zbiorami, można też mówić o zależności (związku) między dwiema zmiennymi ${\displaystyle x}$ i ${\displaystyle y,}$ gdzie pierwsza z nich przyjmuje wartości ze zbioru ${\displaystyle X,}$ a druga przyjmuje wartości ze zbioru ${\displaystyle Y;}$ wtedy ${\displaystyle x}$ nazywa się zmienną niezależną, a ${\displaystyle y}$ – zmienną zależną^[22][23]. Taka interpretacja funkcji jest często używana w analizie matematycznej i zastosowaniach matematyki w innych naukach. W tym wypadku niezależność zmiennej ${\displaystyle x}$ oznacza, że może się ona zmieniać w dowolny sposób, a zależność zmiennej ${\displaystyle y}$ oznacza, że jej zmiany są zależne od zmian zmiennej ${\displaystyle x.}$ Na przykład droga ${\displaystyle s}$ w ruchu jednostajnym o prędkości ${\displaystyle v}$ jest zależna od czasu ${\displaystyle t}$ ruchu i wyraża się wzorem:

${\displaystyle s=v\cdot t.}$

W praktyce często się zdarza, że zbiór ${\displaystyle X}$ jest opisywany przez kilka zmiennych niezależnych ${\displaystyle x_{1},\dots ,x_{n}.}$ Mówimy wtedy, że zmienna ${\displaystyle y}$ jest funkcją zmiennych ${\displaystyle x_{1},\dots ,x_{n}.}$ Na przykład siła ${\displaystyle F}$ działająca na ciało jest zależna od masy ${\displaystyle m}$ ciała i jego przyspieszenia ${\displaystyle a{:}}$

${\displaystyle F=m\cdot a.}$

Zastosowania funkcji

W matematyce i informatyce

• analiza matematyczna – są głównym przedmiotem badań;
• pozwoliły zdefiniować jedno z podstawowych pojęć kombinatoryki i teorii mnogości: moc zbioru^[24].
• pojawiają się w logice matematycznej w postaci funkcji zdaniowych (predykatów) i innych funktorów;
• stały się jednym z fundamentów informatyki, gdzie nazywa się tak odmianę procedury; powstałe całe metody programowania oparte na tym pojęciu jak programowanie funkcyjne;.

Definicję funkcji spełniają na przykład:

• działania arytmetyczne: dodawanie, odejmowanie, mnożenie i dzielenie. Można je traktować jako funkcje liczbowe dwóch lub większej liczby zmiennych.
• Jednoargumentowe działania na liczbach: zaokrąglanie, podłoga i sufit oraz część ułamkowa, wartość bezwzględna, liczba przeciwna (przykład funkcji liniowej), liczba odwrotna (przykład funkcji wymiernej),
• średnie: arytmetyczna, geometryczna i inne. To funkcje dwóch lub dowolnej liczby zmiennych. Można je traktować jako funkcje na ciągach lub multizbiorach liczb.
• inne funkcje statystyczne, np. mediana, moda, minimum i maksimum,
• funkcje teorioliczbowe: największy wspólny dzielnik i najmniejsza wspólna wielokrotność dwóch lub więcej liczb całkowitych,
• przekształcenia geometryczne: odbicie względem prostej lub punktu i inne symetrie, obrót względem punktu lub osi, jednokładność, dylatacja, inwersja i wiele innych,
• odległość między punktami (w ogólności metryka), długość wektora (w ogólności norma),
• Średnica zbioru – funkcja ze zbioru potęgowego dowolnej przestrzeni metrycznej,
• długość linii (łamanej lub ogólnie krzywej), w szczególności obwód dla krzywych zamkniętych,
• pole powierzchni, objętość, prawdopodobieństwo i inne przykłady miary.
• działania na zdaniach lub formułach: negacja, implikacja, alternatywa, alternatywa rozłączna, koniunkcja, dysjunkcja, równoważność,
• same formuły zdaniowe: przyporządkowanie termom zdania,
• wartość logiczna,
• działania na zbiorach,
• działania na ciągach skończonych, jak permutacja (np. inwersja) oraz konkatenacja,
• układ współrzędnych to funkcja z przestrzeni geometrycznej (zwłaszcza rozmaitości) w przestrzeń kartezjańską.

W fizyce

Zobacz też: zmienne zależna i niezależna.

Wszystkie wielkości fizyczne rozpatruje się jako funkcje innych zmiennych:

• Jednostki fizyczne są często funkcjami liniowymi innych jednostek, np. temperatura w skali Fahrenehita jest liniową funkcją tej Celsjusza.
• Czasami jednostki są logarytmicznymi funkcjami innych jednostek, np. poziom natężenia dźwięku, wysokość dźwięku, jasność absolutna,
• W statyce: przyporządkowanie każdemu ciału fizycznemu jego masy oraz środka masy. Zgodnie z prawem Hooke’a siła nacisku lub naciągu jest proporcjonalna do odkształcenia ciała (dla odpowiednio małych wartości tych parametrów). To funkcje liniowe siebie nawzajem. Ich zależność opisują współczynnik sprężystości, moduł Younga i inne. Tarcie jest liniową funkcją siły nacisku.
• W kinematyce: ruch ciał fizycznych opisywany jest przez wektor położenia lub przemieszczenia ${\displaystyle {\vec {r}}}$ oraz skalary odległości lub drogi s. Wszystkie są funkcjami czasu. Ta pierwsza to tzw. trajektoria lub linia świata. Na ich podstawie są oparte inne funkcje czasu: prędkość i przyspieszenie.
• W dynamice: pęd jest funkcją dwóch zmiennych: masy i prędkości, przy czym obydwie mogą być funkcjami czasu. Siła okazuje się pochodną pędu po czasie (II zasada dynamiki). Praca jest funkcją siły i przesunięcia ciała, a energia może być zależna od różnych wielkości. Energia kinetyczna ruchu ciała jest zależna od masy ciała i jego prędkości; energia potencjalna grawitacji jest (w przypadku grawitacji ziemskiej) zależna od masy ciała i jego odległości h od powierzchni Ziemi; przyrost energii cieplnej cieczy jest funkcją masy cieczy i przyrostu jej temperatury T
• W bardziej zaawansowanej mechanice definiuje się też inne wielkości dynamiczne: lagranżjan, działanie i hamiltonian, które też są funkcjami mas, położeń i prędkości.
• Liczne pola fizyczne: funkcje z przestrzeni lub czasoprzestrzeni w zbiór skalarów, wektorów, tensorów itp.
• prąd jest funkcją napięcia – w prostych wypadkach opisywaną przez prawo Ohma.
• W termodynamice: objętość ciał oraz ich gęstość jest funkcją temperatury – rozszerzalność cieplna
• W mechanice kwantowej wektor stanu bywa funkcją, a konkretniej zespolonym polem skalarnym – tzw. funkcja falowa.
• Tensory: formy wieloliniowe, czyli funkcje wielu wektorów i kowektorów. Są używane w statyce (wytrzymałość materiałów), w optyce (dwójłomność) oraz w ogólnej teorii względności Einsteina.

W innych dziedzinach

Funkcja może wyrażać własność pewnego obiektu, dlatego obejmuje bardzo wiele pojęć z nauk empirycznych. Jako funkcję można też traktować każdą relację równoważności zachodzącą między dokładnie dwoma obiektami – jest to tzw. inwolucja.

Astronomia:

• położenie ciał niebieskich na niebie (współrzędne astronomiczne) jest funkcją czasu oraz współrzędnych geograficznych,
• okres obiegu planety wokół Słońca jest malejącą funkcją promienia jej orbity, zgodnie z III prawem Keplera,
• jasność obserwowana gwiazdy jest funkcją jej jasności absolutnej i odległości od obserwatora,
• krzywa rotacji galaktyki – prędkość gwiazdy względem galaktyki jest funkcją odległości od jej środka,
• przesunięcie ku czerwieni widm odległych galaktyk jest funkcją ich odległości od Ziemi – zgodnie z prawem Hubble’a,
• Diagram HR opisuje moc promieniowania i temperaturę gwiazdy w funkcji czasu.

Chemia:

• Przykładowo liczba atomowa, blok, grupa i okres w UOP albo liczba elektronów walencyjnych to funkcje na zbiorze pierwiastków chemicznych. Ta pierwsza jest różnowartościowa, a pozostałe – nie.
• liczba masowa i liczba neutronowa to funkcje na zbiorze nuklidów (wszystkie izotopy wszystkich pierwiastków),
• masa cząsteczkowa – funkcja na zbiorze molekuł albo związków,
• jądro lustrzane – bijekcja w zbiorze nuklidów,
• odbicie lustrzane – bijekcja w zbiorze cząsteczek chiralnych,
• własności makroskopowe subtancji jak temperatura wrzenia, temperatura topnienia itp.,
• skala pH jest logarytmiczną funkcją altywności jonów hydroniowych.

Biologia:

• Przykładem nieliczbowej funkcji jest kod genetyczny. Zgodnie z zasadą szufladkową Dirichleta nie może być funkcją różnowartościową, czyli innymi słowy jest zdegenerowany.
• mutacje genowe – zmiana sekwencji nukleotydów, np. substytucja, delecja, insercja,
• komplementarny nukleotyd lub cała nić DNA,
• krzywa wzrostu i inne parametry populacji.

Medycyna i fizjologia:

• BMI – funkcja dwóch zmiennych: wzrostu i wagi
• EKG i EEG – funkcje napięcia między elektrodami od czasu,

Geografia fizyczna, geodezja i inne nauki o Ziemi:

• wysokość bezwzględna, temperatura, ciśnienie atmosferyczne, a dla zbiorków wodnych zasolenie – funkcje współrzędnych geograficznych. To przykłady funkcji wielu zmiennych – konkretniej pól skalarnych.
• Temperatura i ciśnienie są też funkcją współrzędnych geograficznych i wysokości bezwzględnej,
• średnia temperatura atmosfery ziemskiej jest od XX w. funkcją rosnącą – globalne ocieplenie.

Geografia społeczna, demografia i socjologia:

• piramida wieku danemu wiekowi lub przedziałowi wieku przyporządkowuje odsetek osób w tym wieku. Dla społeczeństw młodych jest to funkcja malejąca. Niże i echa niżów demograficznych to lokalne minima tej funkcji.
• opinia publiczna, np. procentowe poparcie dla danej opcji politycznej albo decyzji jest funkcją czasu, a także wieku, płci i regionu.

Ekonomia:

• funkcje podaży i popytu,
• cena, np. kurs walutowy,
• rozmaite parametry gospodarki: PKB, inflacja, dług publiczny, HDI itd. Można je traktować jako funkcje na zbiorze państw, a dla danego państwa: funkcje od czasu.
• Liczne krzywe ekonomiczne, np. Laffera i Phillipsa

Psychologia:

• wyniki testów IQ są rosnącą funkcją czasu – efekt Flynna,
• funkcja komfortu psychicznego obserwatora od podobieństwa androida do człowieka ma lokalne minimum – to tzw. dolina niesamowitości,
• wiele wyników testów psychometrycznych w populacji, np. IQ i EQ jest opisanych funkcją rozkładu normalnego.

Pojęcia

Złożenie. Iteracja

Osobny artykuł: złożenie funkcji.

Dwie funkcje ${\displaystyle f}$ i ${\displaystyle g.}$ Ich złożenie przyjmuje wartości:
${\displaystyle (g\circ f)(\mathrm {a} )=}$ @
${\displaystyle (g\circ f)(\mathrm {b} )=}$ @
${\displaystyle (g\circ f)(\mathrm {c} )=\#}$
${\displaystyle (g\circ f)(\mathrm {d} )=\$ !!}

Mając dwie funkcje ${\displaystyle f\colon X\to Y}$ i ${\displaystyle g\colon Y\to Z,}$ można utworzyć funkcję złożoną ${\displaystyle (g\circ f)\colon X\to Z}$ określoną wzorem ${\displaystyle (g\circ f)(x)=g{\Big (}f(x){\Big )}.}$

Wielokrotne złożenie funkcji ${\displaystyle f\colon X\to X}$ nosi nazwę iteracji. Ściśle: ${\displaystyle n}$-tą iteracją funkcji ${\displaystyle f}$ nazywa się funkcję

${\displaystyle f^{n}={\begin{matrix}\underbrace {f\circ f\circ \ldots \circ f} \\{n}\\[-4ex]\end{matrix}}.}$

Funkcja odwrotna

Osobny artykuł: funkcja odwrotna.

Dla każdej funkcji wzajemnie jednoznacznej można określić funkcję ${\displaystyle f^{-1}\colon Y\to X}$ taką, że ${\displaystyle (f\circ f^{-1})(x)=x,}$ którą nazywa się wówczas funkcją odwrotną.

W definicji Bourbakiego, dla funkcji ${\displaystyle f=(X,Y,W)}$ utworzmy trójkę ${\displaystyle f^{-1}=(Y,X,W^{-1})}$, gdzie ${\displaystyle W^{-1}=\{(y,x):(x,y)\in W\}}$. Jeżeli trójka ${\displaystyle f^{-1}}$ jest funkcją, to jest to funkcja odwrotna do ${\displaystyle f}$. Aby funkcja odwrotna istniała ${\displaystyle f}$ musi być bijekcją.

Zawężenie i przedłużenie

Osobny artykuł: Restrykcja funkcji.

Dla funkcji ${\displaystyle f\colon X\to Y}$ można określić jej zawężenie, nazywane też obcięciem lub ograniczeniem, do zbioru ${\displaystyle M\subseteq X.}$ Jest to funkcja ${\displaystyle f|_{M}\colon M\to Y}$ taka, że ${\displaystyle f|_{M}(x)=f(x)}$ dla każdego ${\displaystyle x\in M.}$ Nazywa się ją też funkcją częściową dla funkcji f^[25].

Jeżeli ${\displaystyle f\colon X\to Y}$ jest funkcją, a ${\displaystyle f|_{M}\colon M\to Y}$ jest jej zawężeniem do zbioru ${\displaystyle M\subset X,}$ to dla dowolnego zbioru ${\displaystyle B\subset Y}$ mamy ${\displaystyle \left(f|_{M}\right)^{-1}(B)=M\cap f^{-1}(B).}$

Z drugiej strony, dla ${\displaystyle M\subset X,}$ można przedłużyć funkcję ${\displaystyle f\colon M\to Y}$ zachowawszy często pewną regułę, otrzymując w ten sposób funkcję ${\displaystyle g\colon X\to Y.}$ Można np. wymagać, by przedłużenie ${\displaystyle g}$ funkcji ${\displaystyle f}$ było ciągłe, różniczkowalne lub okresowe.

Współczesne definicje

Funkcja jako pojęcie matematyczne używane było w co najmniej dwóch zbliżonych znaczeniach:

• dla danych dwóch zbiorów ${\displaystyle X}$ i ${\displaystyle Y}$ funkcją nazywano każde przyporządkowanie^[b] elementom zbioru ${\displaystyle X}$ po jednym elemencie zbioru ${\displaystyle Y}$^[c][17];
• zazwyczaj wymaga się też, aby to przypisanie dotyczyło każdego elementu zbioru ${\displaystyle X}$^[6]. Wtedy obiekty spełniające tylko pierwszy warunek są znane jako funkcje częściowe.

Definicja Bourbakiego i jej alternatywne formy

Definicja ${\displaystyle f=(X,Y,W)}$ Bourbakiego^[7][8], ze względu na prostotę, pełność i ogólność spełnia wymogi współczesnej matematyki^[26]. W literaturze definicja może różnić się kolejnością elementów np. ${\displaystyle f=(W,X,Y)}$ albo ${\displaystyle f=(X,W,Y)}$. Spotyka się również wariant tej definicji w której używa się klas zamiast zbiorów^[9].

Definicja Peana

Jeżeli zakładamy że funkcja jest surjekcją lub jeśli jest wygodne nie ustalanie przeciwdziedziny, wówczas można skorzystać z definicji Peana redukującej funkcję tylko do wykresu funkcji (wykresu z definicji Bourbakiego) tj. ${\displaystyle f=W}$ (a więc do pewnego zbioru par). Tak zredukowana definicja jest bardziej pierwotna i została sformalizowana wcześniej. Często w literaturze zaznacza się (z przyczyn głównie historycznych związanych z oryginalnym sformułowaniem Peana), że taka zredukowana definicja (wykres) jest pewną relacją binarną. Relacja ${\displaystyle R}$ jest funkcją, jeśli spełnia dwa warunki, poniżej zapisane za pomocą kwantyfikatorów^[2]:

1. jednoznaczność^[27]: ${\displaystyle \forall x\in X,y_{1},y_{2}\in Y:[xRy_{1}\wedge xRy_{2}\Rightarrow (y_{1}=y_{2})],}$
2. ${\displaystyle \forall x\in X\ \exists y\in Y:xRy.}$

Przez to funkcje – rozumiane szeroko – są też znane jako relacje jednoznaczne^[28]. Podana własność jest też znana jako jednoznaczność prawostronna^[29].

Teoria mnogości definiuje relacje za pomocą iloczynu kartezjańskiego zbiorów, czyli zbioru par uporządkowanych: ${\displaystyle R\subseteq X\times Y.}$

Porównanie

Należy zauważyć że między definicją Bourbakiego ${\displaystyle f=(X,Y,W)}$ a definicją Peana ${\displaystyle f=W}$ istnieją poważne różnice^[30] (obydwie jednak, są powszechnie używane w literaturze^[26]) np.:

• w def. Bourbakiego funkcja jest trójką, natomiast w def. Peana jest zbiorem par - a więc są różnymi obiektami
• niech ${\displaystyle W^{-1}=\{(y,x):(x,y)\in W\}}$, wówczas w definicji Peana funkcja odwrota to ${\displaystyle f^{-1}=W^{-1}}$ i istnieje ona tylko wtedy gdy ${\displaystyle f}$ jest różnowartościowa, natomaist w definicji Bourbakiego ${\displaystyle f^{-1}=(Y,X,W^{-1})}$ i istnieje ona tylko, gdy f jest różnowartościowa oraz "na".

Rys historyczny

Poszukiwaniem wzajemnych zależności między różnymi wielkościami zajmowali się już starożytni Grecy, którzy badali dość szeroki krąg zależności funkcyjnych. Pojęcie funkcji w postaci początkowej pojawiało się w średniowieczu, lecz dopiero w pracach matematyków XVII wieku, Fermata, Kartezjusza, Newtona i Leibniza, zaczęło być traktowane jako obiekt badań.

Termin funkcja pojawił się w matematyce w XVII wieku, po czym kolejni uczeni nadawali mu nowe znaczenia^[6]. Leonhard Euler w osiemnastym wieku był pierwszym matematykiem, który użył wpółczesnego oznaczenia funkcji^[31]. Euler używał dwóch definicji funkcji, pierwsze jako analityczne wyrażenie (formuła), zawierajaca stałe oraz zmienne. Druga definicja to zmienna zależna od innej zmiennej. Takie samo podejście można znaleźć w książkach Lagrange’a. Drugie podejście, z drobnymi zmianami, było używane przez późniejszych matematyków, takich jak Cauchy, Fourier, Drichlet, czy Riemann^[32].

Newton używał terminu fluenta^[d]. Terminu funkcja użył po raz pierwszy^[33] Leibniz w pracy Odwrotna metoda stycznych lub o funkcjach^[34]. Po raz drugi Leibniz użył tego terminu w dość wąskim znaczeniu w pracy opublikowanej w czasopiśmie „Acta Eruditorum” w 1692 roku i dwa lata później w „Journal des sçavans”. Następnie w tym samym 1694 roku Johann Bernoulli w „Acta Eruditorum”, nie używając co prawda słowa funkcja, oznaczył mimochodem literą n „dowolną wielkość utworzoną z nieoznaczonych i stałych”^[e][35]. Po trzech latach, w tym samym piśmie, Bernoulli wielkości te oznaczał przez X i ${\displaystyle \xi ,}$ a w liście do Leibniza z 26 kwietnia 1698 roku stwierdził, że symbole te są lepsze, bo „od razu jest widoczne, od jakiej zmiennej jest funkcja”. Jeszcze w 1698 roku w korespondencji między oboma uczonymi funkcja była rozumiana jako wyrażenie analityczne i weszły do użytku terminy wielkość zmienna i wielkość stała.

Określenie funkcji jako wyrażenia analitycznego było po raz pierwszy sformułowane w druku w artykule Johanna Bernoulli opublikowanym w 1718 roku. Napisał on:

Definicja. Funkcją wielkości zmiennej nazywa się tutaj wielkość utworzoną w jakikolwiek sposób z tej wielkości zmiennej i stałych^[36].

W tym samym artykule zaproponował on jako „charakterystykę” funkcji grecką literę ${\displaystyle \varphi ,}$ zapisując argument jeszcze bez nawiasów ${\displaystyle \varphi x.}$ Zarówno nawiasy, jak literę f wprowadził Leonhard Euler w 1734 roku.

Definicję relacyjną ok roku 1911 zaproponował Giuseppe Peano^[14][37]; utożsamia ona funkcję z jej wykresem tj. ${\displaystyle f=W}$. Jest użyteczna w tworzeniu systemów aksjomatycznych pewnych teorii, bowiem funkcja jest wtedy pojęciem pochodnym względem aksjomatyki teorii mnogości^{[potrzebny przypis]}.

Współczesna definicja ${\displaystyle f=(X,Y,W)}$ Bourbakiego^[7][8] została wprowadzona w 1954 r.^[38]. Relacyjna definicja Peana oraz pełna definicja Bourbakiego, są powszechnie używane w literaturze^[26].

Zobacz też

Zobacz hasło funkcja w Wikisłowniku

Zobacz podręcznik w Wikibooks: Matematyka dla liceum – Pojęcie funkcji

• rachunek lambda

Uwagi

1. Od fungor, functus sum, fungi „wykonać, wypełnić, zwolnić”.
2. W Słowniku języka polskiego, PWN, 1996: ustalić relację między czymś a czymś, uczynić zależnym od czegoś...
3. Tej szerokiej definicji używali m.in. Giuseppe Peano oraz Kazimierz Kuratowski i Andrzej Mostowski w swojej książce cytowanej poniżej.
4. Dokładniej, po łacinie, fluentes quantitates.
5. ...positio n esse quantitatem quomodocunque formatam ex indeterminatis et constantibus.