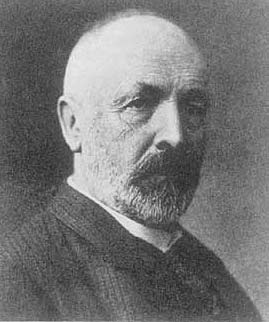Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor (ur. 3 marca 1845 w Petersburgu, zm. 6 stycznia 1918 w sanatorium w Halle) – niemiecki matematyk, profesor Uniwersytetu w Halle, laureat Medalu Sylvestera za rok 1904^[1].

Georg Cantor

Data i miejsce urodzenia	3 marca 1845 Petersburg
Data i miejsce śmierci	6 stycznia 1918 Halle
Zawód, zajęcie	matematyk

Cantor to pionier teorii mnogości, w której m.in. wprowadził ogólne pojęcie mocy zbioru, udowodnił nieprzeliczalność zbioru liczb rzeczywistych^[2] przez rozumowanie przekątniowe, wykazał też ogólniejsze twierdzenie Cantora oraz sformułował hipotezę continuum.

Życiorys

Studiował w Darmstadt, Zurychu i Getyndze. Doktorat obronił w 1867 roku w Berlinie. Do jego nauczycieli należeli: Karl Weierstrass, Ernst Eduard Kummer oraz Leopold Kronecker. Uczył w berlińskim gimnazjum i ponad trzydzieści lat był profesorem uniwersytetu w Halle (Saale). Był zaprzyjaźniony z Richardem Dedekindem. Cantor miał znaczący udział w tworzeniu podwalin nowoczesnej matematyki. W szczególności uchodzi za twórcę teorii mnogości. Ζmarł 6 stycznia 1918 na skutek zawału serca.

Dzieło

Pierwsze prace Cantora dotyczyły teorii liczb. Do stworzenia teorii mnogości doprowadziły go prowadzone przez niego badania dotyczące szeregów trygonometrycznych. Cantor zetknął się w nich z nieskończonymi zbiorami punktów i zwrócił uwagę na ich paradoksalne własności. Zauważył między innymi, że między każdym odcinkiem leżącym na prostej, a tą prostą istnieje wzajemnie jednoznaczna odpowiedniość. Zagadnienia te doprowadziły Cantora do wprowadzenia pojęć równoliczności i mocy zbioru (liczby kardynalnej) – obecnie podstawowych terminów w teorii mnogości. Stosunkowo później Cantor podał następującą definicję zbioru:

Zbiorem jest spojenie w całość określonych rozróżnialnych podmiotów naszej poglądowości czy myśli, które nazywamy elementami danego zbioru.

Obecnie ta definicja nie ma zastosowania – przyjmuje się, że zbiór jest pojęciem pierwotnym.

Kilkanaście lat życia Cantor poświęcił rozwijaniu teorii mnogości, a w tym koncepcji liczb pozaskończonych. Odkrył, że zbiory nieskończone mogą być różnej wielkości – w szczególności odkrył pojęcie przeliczalności i pokazał za pomocą rozumowania przekątniowego, że zbiór liczb naturalnych nie jest równoliczny ze zbiorem liczb rzeczywistych.

Cantor przez długi czas starał się udowodnić hipotezę continuum (jak się okazało w latach 60. XX w. – jego wysiłki nie mogły przynieść zadowalającego go rezultatu). W ostatnich latach swojej pracy naukowej odkrył pewne paradoksy w teorii mnogości. Długie lata cierpiał na ciężkie depresje (parokrotnie był z tego powodu hospitalizowany). Pod koniec życia zajmował się mistycyzmem – rozwijał koncepcję Absolutnej Nieskończoności, którą utożsamiał z Bogiem. Z powodu choroby i niemożności uniknięcia paradoksów zaprzestał publikowania prac naukowych.

Początkowo większość współczesnych Cantorowi matematyków odnosiła się do jego badań bardzo krytycznie (zwłaszcza Leopold Kronecker). Obecnie jednak jego wyniki są nie tylko w pełni akceptowane, ale uznawane za przełomowe w historii matematyki. Dzięki nim mogły rozwinąć się między innymi takie jej dziedziny jak topologia i analiza rzeczywista.

Publikacje

• Über die Ausdehnung eines Satzes aus der Theorie der trigonometrischen Reihen, 1872. (niem.)
• Über die verschiedenen Standpunkte in bezug auf das aktuale Unendliche, 1886. (niem.)
• Über eine elementare Frage der Mannigfaltigkeitslehre, 1890/91. (niem.)
• Beiträge zur Begründung der transfiniten Mengenlehre, 1895-97. (niem.)
• Ex Oriente Lux (dialog), przeł. Tomasz Ososiński, oryg. 1905.

Upamiętnienia

• Ulica Georg-Cantor-Straße w mieście Halle (Saale)^[3]
• Specjalistyczne gimnazium matematyczno-przyrodnicze Georg-Cantor-Gymnasium w mieście Halle (Saale)^[4]
• Stowarzyszenie przyjaciół i mecenasów matematyki i informatyki na Uniwersytecie Marcina Lutra w Halle i Wittenberdze Georg-Cantor-Vereinigung der Freunde und Förderer von Mathematik und Informatik an der Martin-Luther-Universität Halle-Wittenberg e. V.^[5]
• Nazwisko Cantora uwiecznia też Medal Cantora – nagroda dla matematyków niemieckojęzycznych.

Zobacz też

• zbiór Cantora
• twierdzenie Cantora-Bernsteina-Schrödera
• twierdzenie Heinego-Cantora
• Absolutna nieskończoność