Pierwiastek z jedynki

Pierwiastek z jedynki ${\displaystyle n}$-tego stopnia w ciele K – element ${\displaystyle a\in K}$ spełniający równość^[1]:

${\displaystyle a^{n}=1}$

gdzie ${\displaystyle n}$ jest liczbą naturalną większą od 0. Ciałem ${\displaystyle K}$ może być w szczególności ciało liczb zespolonych ${\displaystyle \mathbb {C} }$^[2].

Grupa pierwiastków z jedynki

Zbiór wszystkich pierwiastków z jedynki stopnia ${\displaystyle n}$ tworzy grupę ze względu na mnożenie. Grupa ta jest grupą cykliczną rzędu ${\displaystyle n,}$ zatem jest ona izomorficzna z grupą addytywną klas reszt ${\displaystyle \mathbb {Z} _{n}.}$

Pierwiastki z jedynki w ciele liczb zespolonych

Pierwiastki piątego stopnia z jedynki na płaszczyźnie zespolonej

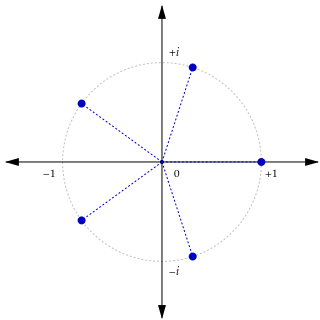
Istnieje dokładnie ${\displaystyle n}$ różnych pierwiastków stopnia ${\displaystyle n}$ z jedynki w zbiorze liczb zespolonych ${\displaystyle \mathbb {C} }$; dane są one wzorami de Moivre'a:

${\displaystyle \omega _{n}^{(k)}=\cos \left({\tfrac {2k\pi }{n}}\right)+i\sin \left({\tfrac {2k\pi }{n}}\right)}$ , ${\displaystyle k=0,1,\dots ,n-1}$

lub równoważnie

${\displaystyle \omega _{n}^{(k)}=e^{\frac {2\pi ik}{n}}}$, ${\displaystyle k=0,1,\dots ,n-1}$

Tradycyjnie liczby ${\displaystyle k=0,1,\dots ,n-1}$ ustanawia się jednocześnie indeksami poszczególnych pierwiastków z jedynki stopnia ${\displaystyle n}$.

Pierwiastki z jedynki w ciele liczb zespolonych nazywane są także liczbami de Moivre’a dla uhonorowania francuskiego matematyka Abrahama de Moivre’a.

Przykłady

Z powyższych wzorów otrzymujemy:

• Pierwiastki 1-go stopnia z jedynki: ${\displaystyle \omega _{0}=1}$
• Pierwiastki 2-go stopnia z jedynki: ${\displaystyle \omega _{0}=1,\ \omega _{1}=-1}$
• Pierwiastki 3-go stopnia z jedynki: ${\displaystyle \omega _{0}=1,\ \ \omega _{1}={\tfrac {-1+i{\sqrt {3}}}{2}},\ \ \omega _{2}={\tfrac {-1-i{\sqrt {3}}}{2}}}$

• Pierwiastki 4-go stopnia z jedynki: ${\displaystyle \omega _{0}=1,\ \ \omega _{1}=i,\ \ \omega _{2}=-1,\ \ \omega _{3}=-i}$

Własności

(1) Na płaszczyźnie zespolonej pierwiastki ${\displaystyle n}$-tego stopnia z jedności są wierzchołkami wielokąta foremnego o ${\displaystyle n}$ bokach wpisanego w okrąg jednostkowy, którego jeden z wierzchołków leży w punkcie ${\displaystyle 1.}$ Realizują one podział tego okręgu na ${\displaystyle n}$ równych części.

(2) Dla ${\displaystyle n>1}$ wszystkie pierwiastki z jedynki ${\displaystyle n}$-tego stopnia sumują się do ${\displaystyle 0{:}}$

${\displaystyle \sum _{k=0}^{n-1}e^{\frac {2\pi ik}{n}}=0}$

(3) Przypadek ${\displaystyle n=2}$ powyższej tożsamości jest znany pod nazwą tożsamości Eulera:

${\displaystyle e^{\pi i}+1=0}$

(4) Grupy ${\displaystyle \mathbb {C} _{n}}$ pierwiastków z jedności ${\displaystyle n}$-tego stopnia wyczerpują skończone podgrupy grupy multiplikatywnej ciała liczb zespolonych. Ważnymi ze względu na klasyfikację grup abelowych są grupy

${\displaystyle \mathbb {C} _{p^{\infty }}{\overset {\underset {\mathrm {def} }{}}{=}}\bigcup _{n=1}^{\infty }~\mathbb {C} _{p^{n}},}$

gdzie ${\displaystyle p}$ jest ustaloną liczbą pierwszą.

Pierwiastki pierwotne z jedynki

Pierwiastki z jedynki stopnia 6-go. Tylko pierwiastek 1-szy i 5-ty są pierwiastkami pierwotnymi (generują wszystkie inne poprzez mnozenie przez siebie).

Df. Pierwiastkami pierwotnymi stopnia ${\displaystyle n}$ z jedynki nazywamy te spośród pierwiastków ${\displaystyle \omega _{n}^{(k)}}$, ${\displaystyle k=0,1,\dots ,n-1}$, które są generatorami grupy, jaką tworzą te pierwiastki. Innymi słowy, wszystkie pozostałe pierwiastki można otrzymać z mnożenia przez siebie generatora odpowiednią ilość razy.

Tw. 1 Dla stopnia ${\displaystyle n}$ pierwiastkiem pierwotnym z jedynki jest na pewno pierwiastek postaci

${\displaystyle \omega =\cos {\frac {2\pi }{n}}+i\sin {\frac {2\pi }{n}}}$

lub równoważnie, w zapisie wykładniczym

${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$

Dowód: Ze wzoru de Moivre'a mamy dla ${\displaystyle k=1,\dots ,n-1}$

${\displaystyle \omega ^{k}=\left(\cos {\frac {2\pi }{n}}+i\sin {\frac {2\pi }{n}}\right)^{\!k}=\cos {\frac {2k\pi }{n}}+i\sin {\frac {2k\pi }{n}}\neq 1}$

zaś dla ${\displaystyle k=n}$ mamy

${\displaystyle \omega ^{n}=\left(\cos {\frac {2\pi }{n}}+i\sin {\frac {2\pi }{n}}\right)^{\!n}=\cos 2\pi +i\sin 2\pi =1,}$

co dowodzi, że ${\displaystyle k=n}$ jest najniższym stopniem, dla którego ${\displaystyle \omega ^{k}=1}$. Oznacza to, że ${\displaystyle \omega =\cos {\tfrac {2\pi }{n}}+i\sin {\tfrac {2\pi }{n}}}$ jest pierwotnym pierwiastkiem z jedynki stopnia ${\displaystyle n}$.

Tw. 2 Pierwiastek stopnia ${\displaystyle n}$ z jedynki o indeksie ${\displaystyle k}$ jest pierwotny, jeżeli liczba ${\displaystyle k}$ jest względnie pierwsza względem stopnia ${\displaystyle n}$ pierwiastka.

Z Tw. 2 wynika stąd, że pierwiastkami prymitywnymi z jedynki są

• 1-go stopnia: ${\displaystyle \omega _{0}=1}$
• 2-go stopnia: ${\displaystyle \omega _{1}=-1}$
• 3-go stopnia: ${\displaystyle \omega _{1}={\tfrac {-1+i{\sqrt {3}}}{2}},\ \ \omega _{2}={\tfrac {-1-i{\sqrt {3}}}{2}}}$

• 4-go stopnia: ${\displaystyle \omega _{1}=i,\ \ \omega _{3}=-i}$
• 5-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{2},\ \ \omega _{3},\ \ \omega _{4}}$
• 6-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{5}}$
• 7-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{2},\ \ \omega _{3},\ \ \omega _{4},\ \ \omega _{5},\ \ \omega _{6}}$
• 8-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{3},\ \ \omega _{5},\ \ \omega _{7}}$
• 9-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{2},\ \ \omega _{4},\ \ \omega _{5},\ \ \omega _{7},\ \ \omega _{8}}$
• 10-go stopnia: ${\displaystyle \omega _{1},\ \ \omega _{3},\ \ \omega _{7},\ \ \omega _{9}}$
• ....

Obliczając liczby pierwiastków dla poszczególnych stopni otrzymamy:

${\displaystyle \varphi (1)=1,\varphi (2)=1,}$ ${\displaystyle \varphi (3)=2,\varphi (4)=2,}$ ${\displaystyle \varphi (5)=4,\varphi (6)=2,}$ ${\displaystyle \varphi (7)=6,\varphi (8)=4,}$ ${\displaystyle \varphi (9)=6,\varphi (10)=4,}$

- zgodnie z funkcją Eulera, co wyraża poniższe twierdzenie.

Tw. 3 Liczba pierwiastków pierwotnych stopnia ${\displaystyle n}$ z jedynki jest równa ${\displaystyle \varphi (n),}$ gdzie ${\displaystyle \varphi }$ jest funkcją Eulera.

Tw. 4 Pierwiastek pierwotny stopnia n z jedynki spełnia równanie algebraiczne stopnia n-1 postaci:

${\displaystyle \omega ^{n-1}+\omega ^{n-2}+\ldots +\omega +1=0}$

Dowód:

Z twierdzenia o sumowaniu się wszystkich pierwiastków stopnia n mamy

${\displaystyle \sum _{k=0}^{n-1}e^{\frac {2\pi ik}{n}}=0}$

Dokonując przekształceń i podstawiając do równania postać wykładniczą pierwiastka pierwotnego ${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$ otrzymamy

${\displaystyle \sum _{k=0}^{n-1}{\Big (}e^{\frac {2\pi i}{n}}{\Big )}^{k}=\sum _{k=0}^{n-1}\omega ^{k}=\omega ^{0}+\omega ^{1}+\ldots +\omega ^{n-1}=0}$

Ponieważ ${\displaystyle \omega ^{0}=1}$, to po zamianie kolejności składników sumy na odwrotny otrzymamy tezę, cnd.

Zobacz też

• addytywna grupa klas reszt
• ciało algebraicznie domknięte
• pierwiastkowanie

Przypisy

1. Browkin 1977 ↓, s. 86.
2. van der Waerden 1967 ↓, s. 153.

Bibliografia

• Jerzy Browkin: Teoria ciał. Warszawa: Państwowe Wydawnictwo Naukowe, 1977, s. 86–88.
• Bartel Leendert van der Waerden: Algebra. Springer-Verlag, 1967., tłum. ros., Москва 1976, s. 153–158.

Literatura dodatkowa

• Bagiński Cz.: Wstęp do teorii grup. Warszawa: SCRIPT, 2005. ISBN 83-904564-9-4. Brak numerów stron w książce

Encyklopedie internetowe (miejsce zerowe):

• Catalana: 0149312