Równoległość

Równoległość – w matematyce jest to wspólna nazwa powiązanych relacji między figurami geometrycznymi jak:

• proste i ich części, np. półproste i odcinki;
• linie krzywe^[1][2];
• płaszczyzny i ich części, np. figury płaskie;
• inne powierzchnie^[3];
• figury w wyższych wymiarach^[a];
• wektory^[4].

Para równoległych prostych oraz para równoległych płaszczyzn. Oprócz tego proste te są równoległe do tych płaszczyzn

Tory kolejowe są budowane z równoległych szyn

Oprócz tego równoległość ma znaczenia mniej matematyczne, bliższe zjawiskom fizycznym – równoległe procesy są przynajmniej częściowo jednoczesne^[5][6].

Definicje

Wektory u i v są nazywane równoległymi, bo ich odpowiednie proste d i d′ są równoległe

Równoległość bywa utożsamiana z rozłącznością – nieprzecinaniem się – dla^[7]:

• prostych na płaszczyźnie;
• płaszczyzn w przestrzeni trójwymiarowej;
• prostej i płaszczyzny^[8].

Przy szerszych definicjach za równoległe uznaje się też:

• proste pokrywające się, inaczej tożsame^[9];
• płaszczyzny pokrywające się^[10];
• prostą i płaszczyznę, na której ona leży^[11].

Analogicznie można definiować równoległość dla obiektów mających więcej wymiarów.

Dla dwóch prostych w trójwymiarze równoległość to więcej niż rozłączność lub równość – ta pierwsza nie jest warunkiem wystarczającym równoległości. Dwie różne proste w trójwymiarze są nazywane równoległymi pod dodatkowym warunkiem, że są współpłaszczyznowe – przechodzi przez nie wspólna płaszczyzna^[12][13]. Proste rozłączne przez to, że nie mają wspólnej płaszczyzny, nazywa się skośnymi^[12].

Równoległość dwóch wektorów w przestrzeni euklidesowej można definiować dwojako – przez:

• równoległość ich prostych;
• ich proporcjonalność wprost – to, że jeden wektor jest przeskalowaniem drugiego.

W pierwszym wypadku równoległość to relacja wyłącznie między wektorami niezerowymi, tj. różnymi od zerowego^[14]. Oprócz tego w trójwymiarze definiuje się iloczyn wektorowy, a równoległość wektorów jest równoważna temu, że ich iloczyn wektorowy jest wektorem zerowym^[15][16]:

${\displaystyle {\vec {u}}\parallel {\vec {v}}\ \Leftrightarrow \ {\vec {u}}\times {\vec {v}}={\vec {0}}.}$

Istnieją także mniej ścisłe definicje, używane w słownikach języka polskiego – odwołują się do równości pewnych odległości między figurami lub przedmiotami^[17][6].

Rola pojęcia

Za pomocą równoległości definiuje się inne pojęcia geometryczne, m.in. planimetrii i stereometrii:

• w geometrii płaskiej równoległością odcinków definiuje się m.in. trapezy^[18] i równoległoboki^[19];
• w geometrii trójwymiarowej równoległość płaszczyzn i odcinków pojawia się w definicjach równoległościanów^[20], bardziej ogólnych graniastosłupów^[21] oraz walców^[22] i powierzchni walcowych^[23].

Oprócz tego równoległość jest też przedmiotem:

• podanego niżej postulatu Euklidesa i jego odmian;
• twierdzenia Talesa^[24].

Geometria euklidesowa

Aksjomaty

Postulat Euklidesa

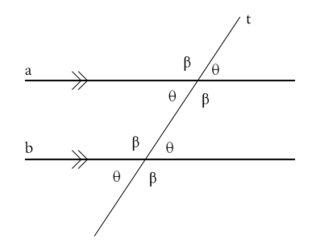
Jeżeli prosta (transwersalna) ${\displaystyle t}$ przecina proste ${\displaystyle a,b}$ tak, że kąty sobie odpowiadające są sobie różne, to proste ${\displaystyle a,b}$ przecinają się. O takich prostych mówi się, że są nierównoległe i oznacza się ${\displaystyle a\nparallel b.}$ Proste, które nie są nierównoległe, nazywane są równoległymi i oznacza się ${\displaystyle a\parallel b.}$

Szkocki matematyk John Playfair określił następujący aksjomat:

Aksjomat Playfaira

Przez dowolny punkt można przeprowadzić najwyżej jedną prostą rozłączną z zadaną prostą. O takiej prostej mówi się, że jest równoległa do zadanej prostej.

Geometrie euklidesowe to geometrie wykorzystujące aksjomat Euklidesa.

Właściwości

Trzy płaszczyzny równoległe parami

Równoległość obiektów tego samego rodzaju – np. między prostymi lub między płaszczyznami – jest relacją równoważności^[25][26], tzn. jest:

• zwrotna: ${\displaystyle a\parallel a,}$
• symetryczna: ${\displaystyle a\parallel b\;{}}$ pociąga ${\displaystyle {}\;b\parallel a,}$
• przechodnia^[12]: jeśli ${\displaystyle a\parallel b\;{}}$ oraz ${\displaystyle {}\;b\parallel c,\;{}}$ to ${\displaystyle {}\;a\parallel c.}$

Planimetria kartezjańska

Na niebiesko zaznaczono parę prostych równoległych na płaszczyźnie kartezjańskiej

Warunki równoległości

Proste zadane równaniami w postaci kierunkowej są równoległe wtedy i tylko wtedy, gdy mają równe współczynniki kierunkowe^[27][28].

Dwie proste na płaszczyźnie kartezjańskiej są interpretacją graficzną układu dwóch równań liniowych z dwiema niewiadomymi. Proste równoległe rozłączne odpowiadają układowi sprzecznemu, proste pokrywające się układowi nieoznaczonemu. Stąd dwie proste zadane równaniami ogólnymi

${\displaystyle {\begin{cases}A_{1}x+B_{1}y+C_{1}=0\\[2pt]A_{2}x+B_{2}y+C_{2}=0\end{cases}}}$

nie przecinają się lub pokrywają się, jeżeli wyznacznik (macierzy głównej) tego układu jest równy zeru^[29]:

${\displaystyle {\begin{vmatrix}A_{1}&B_{1}\\A_{2}&B_{2}\end{vmatrix}}=0\iff A_{1}B_{2}=A_{2}B_{1}.}$

Podobnymi wzorami można sprawdzać równoległość wektorów płaskich^[30].

Odległość prostych równoległych

Jest to odległość któregokolwiek punktu leżącego na jednej prostej od jego rzutu prostopadłego na drugą prostą.

Niech l || k. Wówczas ${\displaystyle l:Ax+By+C_{1}}$ i ${\displaystyle k:Ax+By+C_{2},}$ gdy ${\displaystyle A_{2}+B_{2}>0.}$ Odległość punktu ${\displaystyle O}$ od prostej ${\displaystyle l}$ wyraża się wzorem:

${\displaystyle d={\frac {|Ax_{0}+By_{0}+C_{1}|}{\sqrt {A^{2}+B^{2}}}}.}$

Ponieważ ${\displaystyle O\in k,}$ to ${\displaystyle Ax_{0}+By_{0}+C_{2}=0,}$ więc ${\displaystyle Ax_{0}+By_{0}=-C_{2}.}$

Zatem wzór na odległość dwóch prostych równoległych ma postać^[31]:

${\displaystyle d={\frac {|C_{1}-C_{2}|}{\sqrt {A^{2}+B^{2}}}}.}$

Jeżeli przedstawimy dane proste w postaci kierunkowej: ${\displaystyle l:y=mx+n_{1},}$ ${\displaystyle k:y=mx+n_{2},}$

to wzór przybierze postać:

${\displaystyle d={\frac {|n_{1}-n_{2}|}{\sqrt {1+m^{2}}}}.}$

Geometrie nieeuklidesowe

Ta sekcja jest niekompletna. Jeśli możesz, rozbuduj ją.

Równoległość jest pojęciem charakterystycznym dla geometrii euklidesowej (ogólniej – afinicznej).

W geometrii rzutowej (i geometrii eliptycznej) każde dwie różne proste mają dokładnie jeden punkt wspólny. Nie jest więc spełniony aksjomat Playfaira i nie jest możliwe zdefiniowanie pojęcia równoległości.

W geometrii hiperbolicznej także nie jest spełniony aksjomat Playfaira, tutaj przez dowolny punkt można przeprowadzić (co najmniej) dwie proste rozłączne z zadaną prostą. Można zdefiniować pojęcie równoległości dwóch prostych, odmienne jednak od równoległości definiowanej na płaszczyźnie euklidesowej – np. nie jest to relacja przechodnia.

Zobacz też

Zobacz hasło równoległość w Wikisłowniku

• Przeniesienie równoległe
• obliczenia równoległe
• prostopadłość

Uwagi

1. Ogólniej podprzestrzenie o wymiarze co najwyżej ${\displaystyle n{-}1}$ w przestrzeni ${\displaystyle n}$-wymiarowej.