Треугольная мозаика порядка 8

Треугольная мозаика порядка 8 — это правильная мозаика на гиперболической плоскости. Мозаика имеет символ Шлефли {3,8}, у неё восемь правильных треугольников вокруг каждой вершины.

Треугольная мозаика порядка 8
Тип	Гиперболическая правильная мозаика
Конфигурация вершины	38
Символ Шлефли	{3,8} (3,4,3)
Символ Витхоффа	8 | 3 2 4 | 3 3
Симметрии	[8,3], (*832) [(4,3,3)], (*433) [(4,4,4)], (*444)
Диаграммы Коксетера — Дынкина	или
Двойственные соты	восьмиугольная мозаика?!
Свойства	Изогональная, изотоксальная, изоэдральная

Однородные раскраски

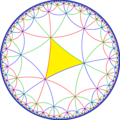
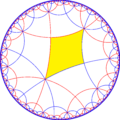
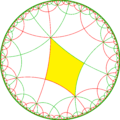
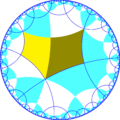
Полусимметрия [1⁺,8,3] = [(4,3,3)] может быть показана чередующейся двухцветной раскраской треугольников:

Симметрия

Восьмиугольная мозаика с *444 зеркалами, .

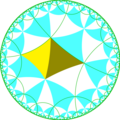
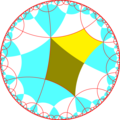
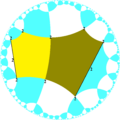
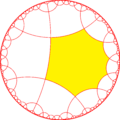
Исходя из симметрии [(4,4,4)], имеется 15 подгупп с малым индексом (7 уникальных), получаемых удалением зеркального отражения и и операцией альтернации^[англ.]. Зеркала могут быть удалены, если их порядки ветвей все чётные, и удаление приводит к уменьшению порядков соседних ветвей вдвое. Удаление двух зеркал оставляет точку вращения половинного порядка в месте пересечения зеркал. На рисунках фундаментальные области выкрашены с чередованием цветов и зеркала находятся на границах между областями разного цвета. Добавление 3 зеркал в каждую фундаментальную область создаёт симметрию 832^[англ.]. Группа с индексом 8 [(1⁺,4,1⁺,4,1⁺,4)] (222222) является коммутантом группы [(4,4,4)].

Подгруппа [(4,4,4^*)] с индексом 8, построенная из (2*2222) путём удаления точек вращения, становится (*22222222).

Симметрия может быть удвоена до симметрии 842 путём добавления зеркал в фундаментальные области.

Подгруппы [(4,4,4)] (*444) с малым индексом

Индек	1	2			4
Диаграмма
Коксетер[англ.]	[(4,4,4)]	[(1+,4,4,4)] =	[(4,1+,4,4)] =	[(4,4,1+,4)] =	[(1+,4,1+,4,4)]	[(4+,4+,4)]
Орбифолд[англ.]	*444	*4242			2*222	222×
Диаграмма
Коксетер		[(4,4+,4)]	[(4,4,4+)]	[(4+,4,4)]	[(4,1+,4,1+,4)]	[(1+,4,4,1+,4)] =
Орбифолд		4*22			2*222
Прямые подгруппы
Индекс	2	4			8
Диаграмма
Коксетер	[(4,4,4)]+	[(4,4+,4)]+ =	[(4,4,4+)]+ =	[(4+,4,4)]+ =	[(4,1+,4,1+,4)]+ =
Орбифолд	444	4242			222222
Радикальные подгруппы
Индекс	8			16
Диаграмма
Коксетер	[(4,4*,4)]	[(4,4,4*)]	[(4*,4,4)]	[(4,4*,4)]+	[(4,4,4*)]+	[(4*,4,4)]+
Орбифолд	*22222222			22222222

Связанные многогранники и мозаики

Соты {3,3,8}^[англ.] имеют вершинные фигуры {3,8}.

*n32 симметрии правильных мозаик: 3ⁿ or {3,n}

Сферическая				Евклидова	Компактная гипербол.		Пара- компактная	Некомпактная гиперболическая
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

Исходя из построения Витхоффа существует десять гиперболических однородных мозаик, которые базируются на правильных мозаиках - восьмиугольной и треугольной порядка 8.

Если рисовать мозаики, выкрашивая красным цветом исходные грани, жёлтым цветом исходные вершины и синим цветом исходные рёбра, получим 10 форм.

Однородные восьмиугольные/треугольные мозаики
Симметрия: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								или	или
Однородные двойственные
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

Правильные мозаики {n,8}
Сферические	Гиперболические мозаики
{2,8}	{3,8}	{4,8}	{5,8}	{6,8}	{7,8}	{8,8}	...	{∞,8}

Мозаика также может быть получена из (4 3 3) гиперболических мозаик:

Однородные мозаики (4,3,3)
Симметрия: [(4,3,3)], (*433)							[(4,3,3)]+, (433)
h{8,3} t0(4,3,3)	r{3,8}1/2 t0,1(4,3,3)	h{8,3} t1(4,3,3)	h2{8,3} t1,2(4,3,3)	{3,8}1/2 t2(4,3,3)	h2{8,3} t0,2(4,3,3)	t{3,8}1/2 t0,1,2(4,3,3)	s{3,8}1/2 s(4,3,3)
Однородные двойственные
V(3.4)3	V3.8.3.8	V(3.4)3	V3.6.4.6	V(3.3)4	V3.6.4.6	V6.6.8	V3.3.3.3.3.4

Однородные мозаики (4,4,4)
Симметрия: [(4,4,4)], (*444)							[(4,4,4)]+ (444)	[(1+,4,4,4)] (*4242)	[(4+,4,4)] (4*22)
t0(4,4,4) h{8,4}	t0,1(4,4,4) h2{8,4}	t1(4,4,4) {4,8}1/2	t1,2(4,4,4) h2{8,4}	t2(4,4,4) h{8,4}	t0,2(4,4,4) r{4,8}1/2	t0,1,2(4,4,4) t{4,8}1/2	s(4,4,4) s{4,8}1/2	h(4,4,4) h{4,8}1/2	hr(4,4,4) hr{4,8}1/2
Однородные двойственные
V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V8.8.8	V3.4.3.4.3.4	V88	V(4,4)3

См. также

• Тетраэдральные соты порядка 8^[англ.]
• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на плоскости^[англ.]
• Список правильных многомерных многогранников и соединений