Восьмиугольная мозаика

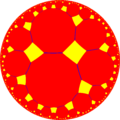
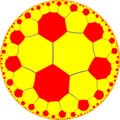
Восьмиугольная мозаика — это правильная мозаика на гиперболической плоскости. Мозаика представлена символом Шлефли {8,3} и имеет три правильных восьмиугольника вокруг каждой вершины. Мозаика также имеет построение в виде усечения квадратной мозаики порядка 8, t{4,8}.

Восьмиугольная мозаика
Тип	Правильная гиперболическая мозаика
Конфигурация вершины	83
Символ Шлефли	{8,3} t{4,8}
Символ Витхоффа	3 | 8 2 2 8 | 4 4 4 4 |
Симметрии	[8,3], (*832) [8,4], (*842) [(4,4,4)], (*444)
Диаграммы Коксетера — Дынкина
Двойственные соты	Треугольная мозаика порядка 8
Свойства	Изогональная, изотоксальная, изоэдральная

Однородные раскраски

Подобно шестиугольной раскраске евклидовой плоскости имеется 3 такие однородные гиперболические раскраски. Двойственная мозаика V8.8.8 представляет фундаментальные области с симметрией [(4,4,4)].

Правильные	Усечения
{8,3}	t{4,8}	t{4[3]} = =
Двойственная раскраска
{3,8} =	=	= =

Правильные карты

Правильную карту {8,3}_2,0 можно рассматривать как 6-цветную раскраску гиперболической мозаики {8,3}. В правильной карте восьмиугольники одного цвета считаются теми же гранями, показанными в разных местах. Нижний индекс 2,0 показывает, что тот же цвет повторяется при движении на пару шагов в сторону противоположного ребра. Эта правильная карта имеет также представление как двойное покрытие куба, что соответствует символу Шлефли {8/2,3}, с 6 восьмиугольными гранями, дважды обёрнутыми {8/2}, с 24 рёбрами и 16 вершинами. Покрытие описано Бранко Грюнбаумом в главе Are Your Polyhedra the Same as My Polyhedra? (Ваш многогранник тот же, что и мой?) книги 2003 года^[1]

Связанные многогранники и мозаики

Эта мозаика топологически является частью последовательности правильных многогранников и мозаик с символом Шлефли {n,3}.

*n32 варианты симметрии правильных мозаик: n³ или {n,3}

Сферические				Евклидовы	Компактные гиперболические.		Параком- пактные.	Некомпактные гиперболические.
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Она также топологически является частью последовательности правильных мозаик с символом Шлефли {8,n}.

Шаблон:Восьмиугольные мозаики

Исходя из построения Витхоффа существует десять гиперболических однородных мозаик, которые базируются на правильных восьмиугольных мозаиках.

Если рисовать мозаики, выкрашивая красным цветом исходные грани, жёлтым цветом исходные вершины и синим цветом исходные рёбра, получим 10 форм.

Однородные восьмиугольные/треугольные мозаики
Симметрия: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								или	или
Однородные двойственные
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

Однородные восьмиугольные/квадратные мозаики
[8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (и подсимметрия [(∞,4,∞,4)] (*4242) )
= = =	=	= = =	=	= =	=
{8,4}	t{8,4}	r{8,4}	2t{8,4}=t{4,8}	2r{8,4}={4,8}	rr{8,4}	tr{8,4}
Однордные двойственные
V84	V4.16.16	V(4.8)2	V8.8.8	V48	V4.4.4.8	V4.8.16
Альтернированные
[1+,8,4] (*444)	[8+,4] (8*2)	[8,1+,4] (*4222)	[8,4+] (4*4)	[8,4,1+] (*882)	[(8,4,2+)] (2*42)	[8,4]+ (842)
=	=	=	=	=	=
h{8,4}	s{8,4}	hr{8,4}	s{4,8}	h{4,8}	hrr{8,4}	sr{8,4}
Альтернированные двойственные
V(4.4)4	V3.(3.8)2	V(4.4.4)2	V(3.4)3	V88	V4.44	V3.3.4.3.8

Однородные мозаики (4,4,4)
Симметрия: [(4,4,4)], (*444)							[(4,4,4)]+ (444)	[(1+,4,4,4)] (*4242)	[(4+,4,4)] (4*22)
t0(4,4,4) h{8,4}	t0,1(4,4,4) h2{8,4}	t1(4,4,4) {4,8}1/2	t1,2(4,4,4) h2{8,4}	t2(4,4,4) h{8,4}	t0,2(4,4,4) r{4,8}1/2	t0,1,2(4,4,4) t{4,8}1/2	s(4,4,4) s{4,8}1/2	h(4,4,4) h{4,8}1/2	hr(4,4,4) hr{4,8}1/2
Однородные двойственные
V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V8.8.8	V3.4.3.4.3.4	V88	V(4,4)3

См. также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на плоскости^[англ.]
• Список правильных многомерных многогранников и соединений