Список k-однородных мозаик

k-Однородные мозаики — это замощение плоскости выпуклыми правильными многоугольниками, соединёнными ребро-к-ребру и имеющими k типов вершин. 1-Однородные мозаики включают 3 правильные мозаики и 8 полуправильных мозаик. 1-Однородные мозаики могут определены их вершинными конфигурациями. Более высокие k-однородные мозаики перечислены по их вершинным фигурам, но они, в общем случае, не определяются уникально таким образом.

Примеры k-однородных мозаик

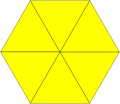
1-однородная (правильная)	1-однородная (полуправильная)
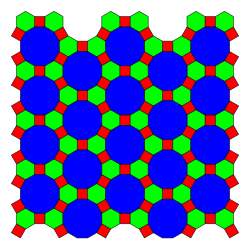
2-однородная мозаика	3-однородная мозаика

Полные списки k-однородных мозаик известны вплоть до k=6. Существует 20 2-однородных мозаик, 61 3-однородная мозаика, 151 4-однородная мозаика, 332 5-однородные мозаики и 673 6-однородные мозаики. Данная статья приводит все решения вплоть до k=5.

Эта квадратная мозаика вершинно транзитивна и гранетранзитивна, но не является однородной, поскольку она не соединена ребро-к-ребру.

Другие замощения правильными многоугольниками не ребро-к-ребру позволяют использование многоугольников других размеров и сдвиг места контакта.

Классификация

3-однородная мозаика №57 (из списка 61 мозаики)

Раскраска по числу сторон - жёлтые треугольники, красные квадраты (по многоугольникам)

Раскраска по 4-изоэдральным позициям, 3 цвета треугольников (по орбитам)

Такие периодические замощения выпуклыми многоугольниками можно классифицировать по числу орбит вершин, рёбер и плиток. Если имеется k орбит вершин, мозаика считается k-однородной или k-вершинно транзитивной; Если имеется t орбит плиток, мозаика считается t-гранетранзитивной; Если имеется e орбит рёбер, мозаика считается e-рёберно транзитивной.

k-однородные мозаики с одинаковой вершинно фигурой можно далее идентифицировать по их симметрии группы орнамента.

Перечисление

1-однородные мозаики вклюяает 3 правильные мозаики и 8 полуправильных с 2 и более типами правильных граней. Имеется 20 2-однородных мозаик, 61 3-однородная мозаика, 151 4-однородная мозаика, 332 5-однородные мозаики и 673 6-однородные мозаики. Мозаики можно сгруппировать по числу m различных вершинных фигур, они называются также m-архимедовыми мозаиками^[1].

Наконец, если число типов верши равно однородности (m = k ниже), то говорят, что это мозаика Кротенхирдта. В общем случае однородность больше либо равна числу типов вершин (m ≥ k), поскольку различные типы вершин обязательно имеют различные орбиты, что в обратную сторону не выполняется. Если положить m = n = k, имеется 11 таких мозаик для n = 1; 20 для n = 2; 39 для n = 3; 33 для n = 4; 15 для n = 5; 10 для n = 6 и 7 таких мозаик для n = 7.

число k-однородных, m-архимедовых мозаик^[2]

		m-архимедовы
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	≥ 15	Всего
k-однородные	1	11	0														11
	2	0	20	0													20
	3	0	22	39	0												61
	4	0	33	85	33	0											151
	5	0	74	149	94	15	0										332
	6	0	100	284	187	92	10	0									673
	7	0	?	?	?	?	?	7	0								?
	8	0	?	?	?	?	?	20	0	0							?
	9	0	?	?	?	?	?	?	8	0	0						?
	10	0	?	?	?	?	?	?	27	0	0	0					?
	11	0	?	?	?	?	?	?	?	1	0	0	0				?
	12	0	?	?	?	?	?	?	?	?	0	0	0	0			?
	13	0	?	?	?	?	?	?	?	?	?	?	?	0	0		?
	14	0	?	?	?	?	?	?	?	?	?	?	?	?	0	0	?
	≥ 15	0	?	?	?	?	?	?	?	?	?	?	?	?	?	0	?
	Всего	11	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	0	∞

1-однородные мозаики (правильные)

Говорят, что мозаика правильная, если группа симметрии мозаики действует транзитивно на флаги мозаики, где флаг — это тройка, состоящая из взаимно инцидентных вершины, ребра и грани. Это означает, что для каждой пары флагов существует операция симметрии, переводящая первый флаг во второй. Это эквивалентно тому, что мозаика состоит из соединённых ребро-к-ребру конгруэнтных правильных многоугольников. Должно быть шесть правильных треугольников, четыре квадрата или три правильных шестиугольника в вершине, в результате получаем три правильных мозаики.

Подробное рассмотрение темы: Список правильных многомерных многогранников и соединений § Евклидовы мозаики

Правильные мозаики (3)

p6m, *632		p4m, *442
36 (t=1, e=1)	63 (t=1, e=1)	44 (t=1, e=1)

m-Архимедовы и k-однородные мозаики

Подробное рассмотрение темы: Список однородных мозаик на евклидовой плоскости

Вершинная транзитивность означает, что для любой пары вершин имеется операция симметрии^[англ.], переводящая первую вершину во вторую^[3].

Если требование транзитивности флагов ослаблено до требования транзитивности вершин при сохранении соединения многоугольников ребро-к-ребру, имеется восемь дополнительных мозаик, известных как архимедовыили однородные. Заметим, что имеется два зеркальных отражения (энантиоморфный или хиральный), образующих 3⁴.6 (плосконосую шестиугольную) мозаику, только одна из которых показана в следующей таблице. Все другие правильные и полуправильные мозаики ахиральны.

Грюнбаум и Шепард примененяют термин архимедова для этих мозаик как ссылку на локальность свойства расположения плиток вокруг вершины, а термин однородная как ссылку на глобальность свойства транзитивности вершин. Хотя на плоскости это приводит к одному и тому же множеству мозаик, в других пространствах есть архимедовы мозаики, не являющиеся однородными.

1-однородные мозаики (полуправильные)

однородные мозаики (8)

p6m, *632
[ 3.122?!] (t=2, e=2)	[ 3.4.6.4] (t=3, e=2)	[ 4.6.12] (t=3, e=3)	[ (3.6)2] (t=2, e=1)
[ 4.82] (t=2, e=2)	[ 32.4.3.4] (t=2, e=2)	[ 33.42] (t=2, e=3)	[ 34.6] (t=3, e=3)

2-однородные мозаики

Имеется двадцать (20) 2-однородных мозаик на евклидовой плоскости (называемых также 2-вершинно транзитивными мозаиками)^[4][5][6] Типы вершин указаны для каждой мозаики. Если две мозаики имеет два одинаковых типа вершин, добавляются индексы 1,2.

2-однородные мозаики (20)

p6m, *632						p4m, *442
[36; 32.4.3.4 (t=3, e=3)	[3.4.6.4; 32.4.3.4] (t=4, e=4)	[3.4.6.4; 33.42] (t=4, e=4)	[3.4.6.4; 3.42.6] (t=5, e=5)	[4.6.12; 3.4.6.4][англ.] (t=4, e=4)	[36; 32.4.12] (t=4, e=4)	[3.12.12; 3.4.3.12][англ.] (t=3, e=3)
p6m, *632	p6, 632	p6, 632	cmm, 2*22	pmm, *2222	cmm, 2*22	pmm, *2222
[36; 32.62] (t=2, e=3)	[36; 34.6]1 (t=3, e=3)	[36; 34.6]2 (t=5, e=7)	[32.62; 34.6] (t=2, e=4)	[3.6.3.6; 32.62] (t=2, e=3)	[3.42.6; 3.6.3.6]2 (t=3, e=4)	[3.42.6; 3.6.3.6]1 (t=4, e=4)
p4g, 4*2	pgg, 22×	cmm, 2*22	cmm, 2*22	pmm, *2222	cmm, 2*22
[33.42; 32.4.3.4]1[англ.] (t=4, e=5)	[33.42; 32.4.3.4]2[англ.] (t=3, e=6)	[44; 33.42]1 (t=2, e=4)	[44; 33.42]2 (t=3, e=5)	[36; 33.42]1 (t=3, e=4)	[36; 33.42]2 (t=4, e=5)

3-однородные мозаики

Имеется 61 3-однородная мозаика на евклидовой плоскости. 39 мозаик являются 3-архимедовы с 3 различными типами вершин, в то время как 22 имеют 2 идентичных типа вершин с различными орбитами симметрии^[7].

3-однородные мозаики, 3 типа вершин

3-однородные мозаики c 3 типами вершин (39)

[3.426; 3.6.3.6; 4.6.12] (t=6, e=7)	[36; 324.12; 4.6.12] (t=5, e=6)	[324.12; 3.4.6.4; 3.122] (t=5, e=6)	[3.4.3.12; 3.4.6.4; 3.122] (t=5, e=6)	[3342; 324.12; 3.4.6.4] (t=6, e=8)
[36; 3342; 324.12] (t=6, e=7)	[36; 324.3.4; 324.12] (t=5, e=6)	[346; 3342; 324.3.4] (t=5, e=6)	[36; 324.3.4; 3.426] (t=5, e=6)	[36; 324.3.4; 3.4.6.4] (t=5, e=6)
[36; 3342; 3.4.6.4] (t=6, e=6)	[36; 324.3.4; 3.4.6.4] (t=6, e=6)	[36; 3342; 324.3.4] (t=4, e=5)	[324.12; 3.4.3.12; 3.122] (t=4, e=7)	[3.4.6.4; 3.426; 44] (t=3, e=4)
[324.3.4; 3.4.6.4; 3.426] (t=4, e=6)	[3342; 324.3.4; 44] (t=4, e=6)	[3.426; 3.6.3.6; 44] (t=5, e=7)	[3.426; 3.6.3.6; 44] (t=6, e=7)	[3.426; 3.6.3.6; 44] (t=4, e=5)
[3.426; 3.6.3.6; 44] (t=4, e=6)	[3342; 3262; 3.426] (t=5, e=8)	[3262; 3.426; 3.6.3.6] (t=4, e=7)	[3262; 3.426; 3.6.3.6] (t=5, e=7)	[346; 3342; 3.426] (t=5, e=7)
[3262; 3.6.3.6; 63] (t=4, e=5)	[3262; 3.6.3.6; 63] (t=2, e=4)	[346; 3262; 63] (t=2, e=5)	[36; 3262; 63] (t=2, e=3)	[36; 346; 3262] (t=5, e=8)
[36; 346; 3262] (t=3, e=5)	[36; 346; 3262] (t=3, e=6)	[36; 346; 3.6.3.6] (t=5, e=6)	[36; 346; 3.6.3.6] (t=4, e=4)	[36; 346; 3.6.3.6] (t=3, e=3)
[36; 3342; 44] (t=4, e=6)	[36; 3342; 44] (t=5, e=7)	[36; 3342; 44] (t=3, e=5)	[36; 3342; 44] (t=4, e=6)

3-однородные мозаики, 2 типа вершин (2:1)

3-однородные мозаики (2:1) (22)

[(3.4.6.4)2; 3.426] (t=6, e=6)	[(36)2; 346] (t=3, e=4)	[(36)2; 346] (t=5, e=5)	[(36)2; 346] (t=7, e=9)	[36; (346)2] (t=4, e=6)
[36; (324.3.4)2] (t=4, e=5)	[(3.426)2; 3.6.3.6] (t=6, e=8)	[3.426; (3.6.3.6)2] (t=4, e=6)	[3.426; (3.6.3.6)2] (t=5, e=6)	[3262; (3.6.3.6)2] (t=3, e=5)
[(346)2; 3.6.3.6] (t=4, e=7)	[(346)2; 3.6.3.6] (t=4, e=7)	[3342; (44)2] (t=4, e=7)	[(3342)2; 44] (t=5, e=7)	[3342; (44)2] (t=3, e=6)
[(3342)2; 44] (t=4, e=6)	[(3342)2; 324.3.4] (t=5, e=8)	[3342; (324.3.4)2] (t=6, e=9)	[36; (3342)2] (t=5, e=7)	[36; (3342)2] (t=4, e=6)
[(36)2; 3342] (t=6, e=7)	[(36)2; 3342] (t=5, e=6)

4-однородные мозаики

Имеется 151 4-однородные мозаики на евклидовой плоскости. Поиск, проведённый Брайаном Галебахом, воспроизвёл список Кротенхирдта из 33 4-однородных мозаик с 4 различными типами вершин, как и списки 85 мозаик с 3 типами вершин и 33 с 2 типами вершин.

4-однородные мозаики, 4 типа вершин

Имеется 33 мозаики с 4 типами вершин.

4-однородные мозаики с 4 типами вершин (33)

[33434; 3262; 3446; 63]	[3342; 3262; 3446; 46.12]	[33434; 3262; 3446; 46.12]	[36; 3342; 33434; 334.12]	[36; 33434; 334.12; 3.122]
[36; 33434; 343.12; 3.122]	[36; 3342; 33434; 3464]	[36; 3342; 33434; 3464]	[36; 33434; 3464; 3446]	[346; 3262; 3636; 63]
[346; 3262; 3636; 63]	[334.12; 343.12; 3464; 46.12]	[3342; 334.12; 343.12; 3.122]	[3342; 334.12; 343.12; 44]	[3342; 334.12; 343.12; 3.122]
[36; 3342; 33434; 44]	[33434; 3262; 3464; 3446]	[36; 3342; 3446; 3636]	[36; 346; 3446; 3636]	[36; 346; 3446; 3636]
[36; 346; 3342; 3446]	[36; 346; 3342; 3446]	[36; 346; 3262; 63]	[36; 346; 3262; 63]	[36; 346; 3262; 63]
[36; 346; 3262; 63]	[36; 346; 3262; 3636]	[3342; 3262; 3446; 63]	[3342; 3262; 3446; 63]	[3262; 3446; 3636; 44]
[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]

4-однородные мозаики, 3 типа вершин (2:1:1)

Имеется 85 мозаик с 3 типами вершин.

4-однородные мозаики (2:1:1)

[3464; (3446)2; 46.12]	[3464; 3446; (46.12)2]	[334.12; 3464; (3.122)2]	[343.12; 3464; (3.122)2]	[33434; 343.12; (3464)2]
[(36)2; 3342; 334.12]	[(3464)2; 3446; 3636]	[3464; 3446; (3636)2]	[3464; (3446)2; 3636]	[(36)2; 3342; 33434]
[(36)2; 3342; 33434]	[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (3262)2; 63]	[36; (3262)2; 63]
[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (346)2; 3262]	[36; (3262)2; 3636]	[(346)2; 3262; 63]
[(346)2; 3262; 63]	[346; 3262; (3636)2]	[346; 3262; (3636)2]	[3342; 33434; (3464)2]	[36; 33434; (3464)2]
[36; (33434)2; 3464]	[36; (3342)2; 3464]	[(3464)2; 3446; 3636]	[346; (33434)2; 3446]	[36; 3342; (33434)2]
[36; 3342; (33434)2]	[(3342)2; 33434; 44]	[(3342)2; 33434; 44]	[3464; (3446)2; 44]	[33434; (334.12)2; 343.12]
[36; (3262)2; 63]	[36; (3262)2; 63]	[36; 346; (3262)2]	[(36)2; 346; 3262]	[(36)2; 346; 3262]
[(36)2; 346; 3636]	[346; (3262)2; 3636]	[346; (3262)2; 3636]	[(346)2; 3262; 3636]	[(346)2; 3262; 3636]
[36; 346; (3636)2]	[3262; (3636)2; 63]	[3262; (3636)2; 63]	[(3262)2; 3636; 63]	[3262; 3636; (63)2]
[346; 3262; (63)2]	[346; (3262)2; 3636]	[3262; 3446; (3636)2]	[3262; 3446; (3636)2]	[346; (3342)2; 3636]
[346; (3342)2; 3636]	[346; 3342; (3446)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]
[3446; 3636; (44)2]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]
[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[3446; (3636)2; 44]
[3446; (3636)2; 44]	[3446; (3636)2; 44]	[3446; (3636)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]
[36; (3342)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]	[36; (3342)2; 44]	[36; (3342)2; 44]
[36; (3342)2; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]

4-однородные мозаики, 2 типа вершин (2:2) и (3:1)

Имеется 33 мозаики с 2 типами вершин, 12 с двумя парами типов и 21 с отношением типов 3:1.

4-однородные мозаики (2:2)

[(3464)2; (46.12)2]	[(33434)2; (3464)2]	[(33434)2; (3464)2]	[(346)2; (3636)2]	[(36)2; (346)2]
[(3342)2; (33434)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(36)2; (3342)2]
[(36)2; (3342)2]	[(36)2; (3342)2]

4-однородные мозаики (3:1)

[343.12; (3.122)3]	[(346)3; 3636]	[36; (346)3]	[(36)3; 346]	[(36)3; 346]
[(3342)3; 33434]	[3342; (33434)3]	[3446; (3636)3]	[3446; (3636)3]	[3262; (3636)3]
[3262; (3636)3]	[3342; (44)3]	[3342; (44)3]	[(3342)3; 44]	[(3342)3; 44]
[(3342)3; 44]	[36; (3342)3]	[36; (3342)3]	[36; (3342)3]	[(36)3; 3342]
[(36)3; 3342]

5-однородные мозаики

Имеется 332 5-однородные мозаики на евклидовой плоскости. Поиск, проведённый Брайаном Галебахом, воспроизвёл список Кротенхирдта из 332 5-однородных мозаик с типами вершин от 2 до 5. Имеется 74 мозаики с 2 типами вершин, 149 мозаик с 3 типами вершин, 94 мозаик с 4 типами вершин и 15 с 5 типами.

5-однородные мозаики, 5 типов вершин

Имеется 15 5-однородных мозаик с 5 типами вершинных фигур.

5-однородные мозаики, 5 types

[33434; 3262; 3464; 3446; 63]	[36; 346; 3262; 3636; 63]	[36; 346; 3342; 3446; 46.12]	[346; 3342; 33434; 3446; 44]	[36; 33434; 3464; 3446; 3636]
[36; 346; 3464; 3446; 3636]	[33434; 334.12; 3464; 3.12.12; 46.12]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]
[36; 346; 3446; 3636; 44]	[36; 3342; 3446; 3636; 44]	[36; 346; 3342; 3446; 44]	[36; 3342; 3262; 3446; 3636]	[36; 346; 3342; 3262; 3446]

5-однородные мозаики, 4 типа вершин (2:1:1:1)

Имеется 94 5-однородные мозаики с 4 типами вершин.

5-однородные мозаики (2:1:1:1)

[36; 33434; (3446)2; 46.12]	[36; 33434; 3446; (46.12)2]	[36; 33434; 3464; (46.12)2]	[36; 3342; (334.12)2; 3464]	[36; (3342)2; 334.12; 3464]
[36; 33434; (334.12)2; 3464]	[36; 33434; 334.12; (3.12.12)2]	[36; 346; (3342)2; 334.12]	[36; 33434; 343.12; (3.12.12)2]	[(3342)2; 334.12; 343.12; 3.12.12]
[(3342)2; 334.12; 343.12; 3.12.12]	[(3342)2; 334.12; 343.12; 44]	[33434; 3262; (3446)2; 44]	[36; (3342)2; 33434; 44]	[346; (3342)2; 33434; 44]
[36; 3342; (3464)2; 3446]	[3342; 3262; 3464; (3446)2]	[33434; 3262; 3464; (3446)2]	[36; 33434; (3446)2; 3636]	[3342; 33434; 3464; (3446)2]
[36; 33434; (3262)2; 3446]	[3342; 3262; (3464)2; 3446]	[33434; 3262; (3464)2; 3446]	[346; 3342; (3464)2; 3446]	[36; (3342)2; 33434; 3464]
[36; (3342)2; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 334.12]
[36; 33434; (334.12)2; 343.12]	[(36)2; 346; 3342; 33434]	[(36)2; 346; 3262; 63]	[36; (346)2; 3262; 63]	[(36)2; 346; 3262; 3636]
[36; 346; (3262)2; 3636]	[36; (346)2; 3262; 3636]	[(36)2; 346; 3262; 3636]	[36; 346; 3262; (3636)2]	[36; (346)2; 3262; 3636]
[36; (346)2; 3262; 3636]	[36; (346)2; 3262; 3636]	[36; 346; (3262)2; 3636]	[36; 346; (3262)2; 3636]	[36; 346; 3262; (63)2]
[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]	[(346)2; 3262; 3636; 63]	[(36)2; 346; 3262; 63]	[(36)2; 346; 3262; 63]
[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]
[346; (3262)2; 3636; 63]	[346; (3262)2; 3636; 63]	[346; 3262; 3636; (63)2]	[346; (3262)2; 3636; 63]	[3342; 3262; 3446; (63)2]
[3342; 3262; 3446; (63)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]	[3262; 3446; (3636)2; 44]
[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]
[3262; 3446; (3636)2; 44]	[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[346; (3342)2; 3636; 44]	[36; 3342; (3446)2; 3636]
[346; (3342)2; 3446; 3636]	[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[36; 3342; (3446)2; 3636]	[346; (3342)2; 3446; 3636]
[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[(36)2; 3342; 3446; 3636]	[36; 3342; 3446; (3636)2]	[346; 3342; (3446)2; 3636]
[36; 346; (3342)2; 3446]	[346; (3342)2; 3262; 3636]	[346; (3342)2; 3262; 3636]	[36; (346)2; 3342; 3446]	[36; (346)2; 3342; 3446]
[36; (346)2; 3342; 3446]	[36; 346; (3342)2; 3262]	[(36)2; 346; 3342; 3636]	[(36)2; 346; 3342; 3636]

5-однородные мозаики, 3 типа вершин (3:1:1) и (2:2:1)

Имеется 149 5-однородных мозаик, 60 имеют копии 3:1:1, 89 имеют копии 2:2:1.

5-однородные мозаикиs (3:1:1)

[36; 334.12; (46.12)3]	[3464; 3446; (46.12)3]	[36; (334.12)3; 46.12]	[334.12; 343.12; (3.12.12)3]	[36; (33434)3; 343.12]
[3262; 3636; (63)3]	[346; 3262; (63)3]	[36; (3262)3; 63]	[36; (3262)3; 63]	[3262; (3636)3; 63]
[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]	[3446; (3636)3; 44]
[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[(36)3; 3342; 44]
[(36)3; 3342; 44]	[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]
[(3342)3; 3262; 3446]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]
[3446; (3636)3; 44]	[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(36)3; 3342; 44]	[(36)3; 3342; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(3342)3; 3446; 3636]	[(3342)3; 3446; 3636]	[346; (3342)3; 3446]	[(36)3; 346; 3262]	[(36)3; 346; 3262]
[(36)3; 346; 3262]	[346; (3262)3; 3636]	[346; (3262)3; 3636]	[(346)3; 3262; 3636]	[(346)3; 3262; 3636]
[(36)3; 346; 3262]	[(36)3; 346; 3262]	[(346)3; 3262; 3636]	[36; 346; (3636)3]	[36; 346; (3636)3]
[36; 346; (3636)3]	[36; 346; (3636)3]	[(36)3; 346; 3636]	[(36)3; 346; 3636]	[36; (346)3; 3636]

5-однородные мозаики (2:2:1)

[(3446)2; (3636)2; 46.12]	[(36)2; (3342)2; 3464]	[(3342)2; 334.12; (3464)2]	[36; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]
[3342; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]	[(33434)2; 343.12; (3464)2]	[36; (3262)2; (63)2]	[(3262)2; (3636)2; 63]
[(36)2; (3342)2; 33434]	[(36)2; 3342; (33434)2]	[346; (3342)2; (33434)2]	[(36)2; 3342; (33434)2]	[(36)2; 3342; (33434)2]
[(3262)2; 3636; (63)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[(3446)2; 3636; (44)2]
[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]	[(36)2; 3342; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]
[36; (3342)2; (44)2]	[(36)2; (3342)2; 44]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]
[(36)2; 3342; (44)2]	[36; (3342)2; (44)2]	[36; (3342)2; (44)2]	[(3446)2; 3636; (44)2]	[(36)2; (3342)2; 44]
[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(33434)2; 3262; (3446)2]	[3342; (3262)2; (3446)2]
[3342; (3262)2; (3446)2]	[3262; (3446)2; (3636)2]	[(3262)2; 3446; (3636)2]	[(3262)2; 3446; (3636)2]	[(3464)2; (3446)2; 3636]
[3262; (3446)2; (3636)2]	[3262; (3446)2; (3636)2]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]
[(346)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(346)2; (3342)2; 3446]	[(346)2; 3342; (3446)2]
[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[(36)2; 346; (3262)2]	[(346)2; (3262)2; 63]	[36; (3262)2; (63)2]
[36; (346)2; (3262)2]	[346; (3262)2; (3636)2]	[(346)2; (3262)2; 3636]	[36; (346)2; (3262)2]	[(346)2; 3262; (3636)2]
[(346)2; (3262)2; 3636]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3636]	[(36)2; (346)2; 3636]
[36; (346)2; (3342)2]	[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[36; (346)2; (3262)2]	[346; (3342)2; (3636)2]
[346; (3342)2; (3636)2]	[(36)2; 346; (3636)2]	[(36)2; (346)2; 3636]	[(36)2; 3342; (33434)2]

5-однородные мозаики, 2 типа вершин (4:1) и (3:2)

Имеется 74 5-однородных типов с 2 типами вершин, 27 с 4:1 и 47 с 3:2 копиями каждого типа.

5-однородные мозаики (4:1)

[(3464)4; 46.12]	[343.12; (3.12.12)4]	[36; (33434)4]	[36; (33434)4]	[(36)4; 346]
[(36)4; 346]	[(36)4; 346]	[36; (346)4]	[3262; (3636)4]	[(346)4; 3262]
[(346)4; 3262]	[(346)4; 3636]	[3262; (3636)4]	[3446; (3636)4]	[3446; (3636)4]
[(3342)4; 33434]	[3342; (33434)4]
[3342; (44)4]	[3342; (44)4]	[(3342)4; 44]	[(3342)4; 44]	[(3342)4; 44]
[36; (3342)4]	[36; (3342)4]	[36; (3342)4]	[(36)4; 3342]	[(36)4; 3342]

Имеется 29 5-однородных мозаик с 3 и 2 типами вершинных фигур.

5-однородные мозаики (3:2)

[(3464)2; (46.12)3]	[(3464)2; (46.12)3]	[(3464)3; (3446)2]	[(33434)2; (3464)3]	[(33434)3; (3464)2]
[(36)2; (346)3]	[(36)2; (346)3]	[(36)3; (346)2]	[(36)3; (346)2]	[(36)3; (346)2]
[(36)3; (346)2]	[(36)2; (346)3]	[(36)2; (346)3]	[(36)2; (346)3]
[(3262)2; (3636)3]	[(346)3; (3636)2]	[(346)3; (3636)2]	[(346)2; (3636)3]
[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)2; (3636)3]
[(3342)3; (33434)2]	[(3342)3; (33434)2]	[(3342)2; (33434)3]	[(3342)2; (33434)3]
[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)2; (44)3]
[(3342)3; (44)2]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)3; (44)2]
[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)3; (3342)2]
[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]

Более высокие k-однородные мозаики

k-Однородные мозаики были перечислены вплоть до k=6. Имеется 673 6-однородные мозаики на евклидовой плоскости. Поиск, проведённый Брайаном Галебахом, воспроизвёл список Кротенхирдта из 10 6-однородных мозаик с 6 различными типами вершин, список из 92 с 5 типами вершин, 187 с 4 типами вершин, 284 с 3 типами вершин и 100 с 2 типами вершин.