Лучшие вопросы
Таймлайн
Чат
Перспективы
Усечённая треугольно-шестиугольная мозаика
Из Википедии, свободной энциклопедии
Remove ads
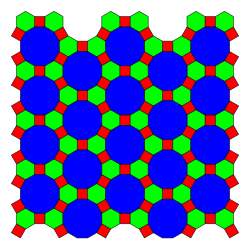
Усечённая треугольно-шестиугольная мозаика — это одна из восьми однородных мозаик на евклидовой плоскости. Мозаика имеет один квадрат, один шестиугольник и один двенадцатиугольник в каждой вершине. Её символ Шлефли tr{3,6}.

Remove ads
Имена
| Название усечённая треугольно-шестиугольная мозаика аналогично названиям Усечённый кубооктаэдр и Ромбоусечённый икосододекаэдр, но в некотором смысле вводит в заблуждение.
Настоящее усечение тришестиугольной мозаики имеет прямоугольники, а не квадраты, а его шестиугольные и двенадцатиугольные грани не могут одновременно быть правильными. Альтернативными взаимозаменяемыми названиями являются: |
Remove ads
Однородная раскраскаs
Существует только одна однородная раскраска усечённой треугольно-шестиугольной мозаики. 2-Однородная раскраска имеет два цвета шестиугольников. 3-Однородная раскраска может иметь 3 цвета двенадцатиугольников и 3 цвета квадратов.
Свазанные 2-однородные мозаики
Усечённая треугольно-шестиугольная мозаика имеет три связанные 2-однородные мозаики[англ.], одной из которых является 2-однородная раскраска полуправильной ромбитришестиугольной мозаики. Первая мозаика разбивает шестиугольники на 6 треугольников. Другие два разбивает двенадцатиугольники на центральный шестиугольник и окружающие его на треугольники и квадраты в двух различных ориентациях[2][3].
Упаковка кругов
Усечённая треугольно-шестиугольная мозаика может быть использована для упаковка кругов, если разместить круги одинакового диаметра с ценрами в каждой точке. Тогда каждый круг соприкасается с 3 другими окружностями в упаковке (контактное число)[4].
Разделенная ромбическая мозаика
Суммиров вкратце
Перспектива
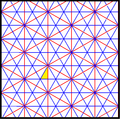
Разделенная ромбическая мозаика или 3-6 разделенная ромбическая мозаика — это мозаика на евклидовой плоскости. Мозаика строится конгруэнтными треугольниками 30-60-90 с 4, 6 и 12 треугольниками в каждой вершине.
Разделение граней этих мозаик создаёт разделенную ромбическую мозаику.
- шестиугольная
- треугольная
(как шестиразделённая шестиугольная) - триразделённая треугольная[англ.]
Разделенная ромбическая мозаика под двойственной ей (слева) и под цветочной пятиугольной мозаикой (справа),
из которой она может быть создана как частичное усечение.
Построение из ромбической мозаики
Конвей называет её kisrhombille[5] (kis означает операцию деления, применённой здесь к ромбической мозаике). Более точно можно назвать её 3-6 разделённой ромбической мозаикой, чтобы отличить её от других похожих гиперболических мозаик, наподобие 3-7 разделённой ромбической мозаики[англ.].
Мозаику можно рассматривать как равностороннюю шестиугольную мозаику с каждым шестиугольником, разделённым на 12 треугольников из центральной точки. (Альтернативно мозаику можно рассматривать как разделённую треугольную мозаику, разделённую на 6 треугольников, или как бесконечная конфигурация прямых из шести параллельных семейств.)
Мозаика обозначена как V4.6.12, поскольку каждая треугольная грань имеет три типа вершин - одна с 4, одна с 6 и одна с 12 треугольниками.
Симметрия
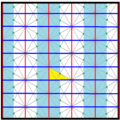
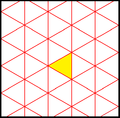
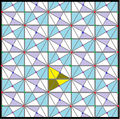
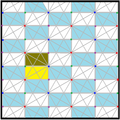
Треугольники разделенной ромбической мозаика представляют фундаментальные области p6m, [6,3] (*632 Орбифолдная нотация[англ.]) симметрии группы обоев. Есть ряд подгрупп с малым индексом, построенных из [6,3] путём удаления зеркал и альтернации. [1+,6,3] образует симметрию *333, показанную как красные линии зеркал. [6,3+] создаёт симметрию 3*3. [6,3]+ является подгруппой вращений. Коммутатором является [1+,6,3+], который имеет симметрию 333. Подгруппа с индексом 6, построенная как [6,3*], также становится (*333), показанной как синие линии зеркал, и она имеет собственную вращательную симметрию 333 с индексом 12.
Remove ads
Связанные многогранники и шаблоны
Существует восемь однородных мозаик, которые могут быть основаны на правильной шестиугольной мозаике (или двойственной треугольной мозаике). Если рисовать плитки красными на месте исходных граней, жёлтым на месте исходных вершин и синим вдоль исходных рёбер, существует 8 форм, 7 из которых топологически различны. (Усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)
Варианты симметрии
Эта мозаика может считаться членом последовательности однородных мозаик с вершинной фигурой (4.6.2p) и диаграммой Коксетера — Дынкина ![]()
![]()
![]()
![]()
![]() .
Для p < 6 членами последовательности являются всеусечённые[англ.] многогранники (зоноэдры),
которые показаны ниже как сферические мозаики.
Для p > 6 мозаики являются гиперболическими, начиная с усечённой треугольно-семиугольной мозаики?!.
.
Для p < 6 членами последовательности являются всеусечённые[англ.] многогранники (зоноэдры),
которые показаны ниже как сферические мозаики.
Для p > 6 мозаики являются гиперболическими, начиная с усечённой треугольно-семиугольной мозаики?!.
Remove ads
См. также
Примечания
Литература
Ссылки
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

 ...
...