Конічні перерізи

Коні́чні пере́різи — невироджені криві, утворені перетином площини з однією або обома частинами конуса. Перетин площиною, перпендикулярною до осі конуса, утворює коло. Перетин площини, не перпендикулярної до осі конуса, з однією з частин конуса утворює еліпс або параболу. Криву, отриману перетином площини з обома частинами конуса, називають гіперболою. Також існують вироджені перерізи: точка, пряма та пара прямих.

Евклідова геометрія

Конічні перерізи вивчалися сотні років і стали джерелом багатьох цікавих відкриттів в евклідовій геометрії.^{[джерело?]}

Визначення

Чорні (частково штрихові) криві, що є межами кольорових областей, є конічними перерізами. На зображенні не показано другу половину гіперболи, яка лежить на другій частині подвоєного конуса, не показаній тут.

Конічний переріз або переріз це крива, що отримується шляхом перетину площини, яку називають січною площиною, і поверхні подвійного конуса (конус із двома симетричними частинами). Для спрощення опису будемо вважати, що це правильний круговий конус, але це не обов'язково, бо поняття є актуальним для будь-якого подвоєного конуса,^[що?] що можна утворити коло при перетині площиною. Площини, що проходять через вершину конуса утворять у перерізі точку, пряму або дві прямі, які перетинаються. Такий випадок називають виродженим і він не становить ніякого інтересу, тому, зазвичай, його не розглядають як конічний переріз. Якщо явно не сказано інше, то під «конічним перерізом» розуміють не вироджені варіанти.

Є три види конічних перерізів, еліпс, парабола, і гіпербола. Коло є частковим випадком еліпса, хоча історично його розглядали як четвертий тип (наприклад, давньогрецький математик Аполлоній). Коло і еліпс виникають коли перетин площини і конуса утворює замкнену криву. Коло утворюється коли січна площина є паралельною площині основного кола, яке утворює конус — для правильного конуса, це означає, що січна площина також перпендикулярна до осі симетрії конуса. Якщо січна площина паралельна до однієї з прямих, які утворюють конус, тоді конічний переріз необмежений і не є замкнений і називається параболою. Залишився ще один варіант перерізу — гіпербола, в цьому випадку січна площина перетне обидві половини конуса, утворюючи окрему необмежену криву.

Ексцентриситет, фокус та директриса

Конічний переріз можна визначити виключно в межах геометрії на площині: це множина всіх точок ${\displaystyle P}$, для яких відношення відстані до фіксованої точки ${\displaystyle F}$ (яку називають фокусом) до відстані до фіксованої прямої ${\displaystyle d}$ (яку називають директрисою) є постійною величиною ${\displaystyle e}$ (яку називають ексцентриситетом).

Коло (e = 0), еліпс (e = 1/2), парабола (e = 1) та гіпербола (e = 2) з фіксованими фокусом F та директрисою. Для точки ${\displaystyle M}$ на еліпсі (e = 1/2): ${\displaystyle |FM|=e\cdot |MM'|}$, де ${\displaystyle MM'}$ перерпендикуляр опущений на ${\displaystyle d}$.

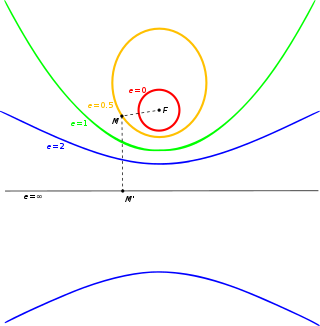
Залежно від значення ексцентриситету, утворюється:

• при ${\displaystyle 0<e<1}$ — еліпс;
• при ${\displaystyle e=1}$ — парабола;
• при ${\displaystyle e>1}$ — гіпербола.

Якщо ${\displaystyle e=0}$, то утворюється коло.

Коло є граничним і не описується фокусом і директрисою на евклідовій площині. Ексцентриситет кола дорівнює нулю, його фокус збігається з центром кола, але його директриса може бути взята тільки як пряма на нескінченності в проєктивній площині.

Ексцентриситет еліпса можна розглядати як міру того, наскільки далеко еліпс відхиляється від кола.

Параметри

Параметри конічних перерізів на прикладі з еліпсом

Існує ряд параметрів, що пов'язані із конічним перерізом. Основною віссю є пряма, що проходить крізь фокуси еліпса або гіперболи, а центр — це середина відрізка прямої, що сполучає фокуси. Нижче наведено деякі спільні поняття і параметри конічних перерізів.^[1]

Лінійний ексцентриситет (позначається буквою ${\displaystyle c}$) — відстань між центром і фокусом (або одним із двох фокусів).

Важливим елементом є хорда, що паралельна директрисі і яка проходить через фокус. Її повна довжина позначається як ${\displaystyle 2\ell }$.

Фокальний параметр (${\displaystyle \ell }$) — половина довжини хорди, що проходить через фокус і паралельна директрисі.

Параметр (${\displaystyle p}$) — відстань від фокуса (або одного з фокусів) до директриси.

Коли еліпс або гіпербола лежать у стандартній позиції (основна вісь збігається з віссю ${\displaystyle x}$, а центр у початку координат) вершини конічних перерізів матимуть координати ${\displaystyle (-a,0)}$ і ${\displaystyle (a,0)}$, де ${\displaystyle a}$ не від'ємні.

Велика піввісь — це значення ${\displaystyle a}$.

Мала піввісь — це значення ${\displaystyle b}$ в рівнянні еліпса або гіперболи на стандартній евклідовій площині.

Виконуються такі рівності:

• ${\displaystyle pe=\ell }$
• ${\displaystyle ae=c.}$

Співвідношення цих параметрів наведено в таблиці нижче, за умови стандартного розташування на координатній площині. В усіх випадках, ${\displaystyle a}$ та ${\displaystyle b}$ додатні.

Конічний переріз	Рівняння	Ексцентриситет (e)	Лінійний ексцентриситет (c)	Половина фокального параметра (ℓ)	Параметр (p)
коло	${\displaystyle x^{2}+y^{2}=a^{2}\,}$	${\displaystyle 0\,}$	${\displaystyle 0\,}$	${\displaystyle a\,}$	${\displaystyle \infty }$
еліпс	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}-b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}}$
парабола	${\displaystyle y^{2}=4ax\,}$	${\displaystyle 1\,}$	-	${\displaystyle 2a\,}$	${\displaystyle 2a\,}$
гіпербола	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}+b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}}$

На декартовій площині

Стандартні форми еліпса

Стандартні форми параболи

Стандартні форми гіперболи

Вибравши декартову систему координат, можна використати фокусу і директрису, аби вивести рівняння, що визначають координати точок конічних перерізів.^[2] Застосовуючи перетворення системи координат, такі як поворот і переміщення осей, ці рівняння можна звести до стандартної форми.^[3] Для еліпсів і гіпербол у стандартній формі декартова вісь x збігається з головною віссю, а початок координат (точка (0,0)) лежить у центрі. Вершини матимуть координати (±a, 0), а фокуси — координати (±c, 0). Визначимо для гіперболи b рівняннями c² = a² − b² для еліпса і c² = a² + b². Для кола, c = 0 тому a² = b². Для параболи, її стандартна форма матиме фокус на осі x в точці (a, 0) а директрисою буде пряма, що задовольняє рівняння x = −a. В стандартній формі парабола завжди проходитиме через початок координат. Особливим випадком гіперболи є ситуація, коли її асимптоти перпендикулярні. В такому випадку гіперболу називають рівнобічною, і стандартну форму можна отримати, прийнявши асимптоти за координатні осі, а пряму x = y за основну вісь. Фокуси матимуть координати (c, c) і (−c, −c).^[4]

• Коло: x² + y² = a²
• Еліпс: x²/a² + y²/b² = 1
• Гіпербола: x²/a² − y²/b² = 1
• Парабола: y² = 4ax, де a > 0
• Рівнобічна гіпербола:^[5] xy = c²/2

Перші три наведені форми є симетричними відносно обох x та y осей (коло, еліпс і гіпербола), або лише відносно осі x (для параболи). Рівнобічна гіпербола, в свою чергу, є симетричною відносно прямих y = x і y = −x.

Ці стандарті форми можна записати у вигляді параметричних рівнянь:

• Коло: (a cos θ, a sin θ),
• Еліпс: (a cos θ, b sin θ),
• Парабола: (at², 2at),
• Гіпербола: (a sec θ, b tan θ) або (±a cosh u, b sinh u),
• Рівнобічна гіпербола: ${\displaystyle \left(dt,{\frac {d}{t}}\right),}$ де ${\displaystyle d={\frac {c}{\sqrt {2}}}.}$

Загальна форма

В системі декартових координат графіком квадратного рівняння двох змінних завжди буде конічний переріз (хоча він може бути виродженим^[6]), і так можна отримати всі конічні перерізи. Загальне рівняння матиме вигляд^[7]

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}$

де всі коефіцієнти — дійсні числа, а A, B, C не дорівнюють нулю.

Отже, конічні перерізи є квадриками.

Дискримінант

Конічні перерізи описані таким рівнянням можна класифікувати в залежності від значення ${\displaystyle B^{2}-4AC}$, що є дискримінантом рівняння.^[8] Тобто, дискримінант дорівнює − 4Δ, де Δ — детермінант матриці ${\displaystyle \left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|.}$

Типи конічних перерізів, залежно від значення дискримінанта, такі:

• Якщо B² − 4AC < 0, то рівняння задає еліпс (вироджені випадки: точка або порожня множина);
  • Якщо A = C і B = 0, то рівняння задає коло, що є частковим випадком еліпса;
• Якщо B² − 4AC = 0, то це парабола, (вироджені випадки: пряма або пара паралельних прямих)
• Якщо B² − 4AC > 0, то це гіпербола або, у виродженому випадку, пара прямих, що перетинаються.
  • Якщо також матимемо A + C = 0, то рівняння задає рівнобічну гіперболу.

В цих позначеннях A і B є коефіцієнтами полінома, не варто їх плутати із позначеннями великої і малої півосей A і B, що використовуються в деяких джерелах.

Матрична нотація

Вище наведене рівняння можна задати в матричному вигляді як^[9]

${\displaystyle \left({\begin{matrix}x&y\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+\left({\begin{matrix}D&E\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+F=0.}$

А також, загальне рівняння можна записати як

${\displaystyle \left({\begin{matrix}x&y&1\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\1\end{matrix}}\right)=0.}$

Ексцентриситет через коефіцієнти рівняння

Якщо конічний переріз задано в алгебраїчній формі як

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,\,}$

ексцентриситет можна визначити як функцію коефіцієнтів квадратичного рівняння.^[10] Якщо 4AC = B², то конічним перерізом є парабола, а її ексцентриситет дорівнює 1 (якщо вона не вироджена). В інших випадках, вважаючи, що рівняння задає невироджені еліпс або гіперболу, ексцентриситет буде задаватися так:

${\displaystyle e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}},}$

де η = 1, якщо детермінант вищезгаданої матриці 3×3 є від'ємним і η = −1, якщо детермінант додатній.

Також можна довести^{[11]:p. 89}, що ексцентриситет є додатним розв'язком рівняння

${\displaystyle \Delta e^{4}+[(A+C)^{2}-4\Delta ]e^{2}-[(A+C)^{2}-4\Delta ]=0,}$

де також ${\displaystyle \Delta =AC-{\frac {B^{2}}{4}}.}$ Воно має рівно один додатний розв'язок — ексцентриситет, у випадку параболи або еліпса, тоді як у випадку з гіперболою воно має два додатні розв'язки, один з яких є ексцентриситетом.

В полярних координатах

В полярних координатах ${\displaystyle (\rho ,\theta )}$ з центром в одному з фокусів та нульовим напрямом вздовж головної осі рівняння конічного перерізу має вигляд:

${\displaystyle \rho (1-e\cos \theta )=l\,}$

де ${\displaystyle e}$ — ексцентриситет, ${\displaystyle l}$ — константа.

Властивості

Конічні перерізи можуть утворюватись як перетин площини і двобічного конуса

${\displaystyle a^{2}z^{2}=x^{2}+y^{2}}$ (в декартових координатах),

де

${\displaystyle a=\operatorname {tg} \theta ,}$

${\displaystyle \theta }$ — кут між твірною конуса та його віссю.

Якщо площина проходить через початок координат, то буде отримано вироджений переріз.

Рівняння конуса квадратичне, тому конічні перерізи є квадриками, також всі квадрики площини є конічними перерізами (хоча дві паралельні прямі утворюють вирождену квадрику яку неможливо отримати перетином конуса, їх вважають «виродженим конічним перерізом»).

Так само як дві (різні) точки визначають пряму, п'ять точок визначають конічний переріз. Через довільні п'ять точок на площині, з яких жодні три не лежать на одній прямій, можна провести єдиний конічний переріз. Формально кажучи, для довільних п'яти точок на площині, що лежать у загальному лінійному положенні, тобто, серед них немає трьох, що були б колінеарними, існуватиме один єдиний конічний переріз, який проходить через них, що не буде виродженим. Це істинне для евклідової площини і для дійсної проєктивної площини. Якщо три точки колінеарні, то конічний переріз, який через них проходить, буде виродженим (оскільки він міститиме пряму), і може бути не єдиним.

Всі конічні перерізи мають спільну властивість відображення, яку можна сформулювати так:

усі дзеркальні поверхні, що мають форму не виродженого конічного перерізу, відбивають світло, що потрапляє в один із фокусів, у бік іншого фокуса.

У випадку з параболою, другий фокус вважають розміщеним у нескінченності, тому промені, що йдуть у напрямку другого фокуса, паралельні.^[12][13]

Теорема Паскаля вивчає колінеарність трьох точок, що побудовані із множини з шести точок на будь-якому не виродженому конічному перерізі. Теорема також справедлива для вироджених конічних перерізів, що складаються із двох прямих, але цей випадок відомий як теорема Паппа.

Невироджений конічний переріз завжди «гладкий». Це є важливою властивістю для багатьох застосувань, наприклад в аеродинаміці, де необхідно мати гладку поверхню, аби бути впевненим в ламінарності течії для уникання турбулентності.

Групи перетворень

• Ексцентриситет двох невироджених конічних перерізів збігається тоді й лише тоді, коли їх можна перевести один в одного перетворенням подібності.
• Афінні перетворення зберігають тільки знак ексцентриситету, тобто, для афінної геометрії існують лише три різні невироджені конічні перерізи: еліпс, парабола та гіпербола.
• У проєктивній геометрії неможливо розрізнити всі невироджені конічні перерізи.

Історія

Конічні перерізи були відомі ще математикам Давньої Греції. Менехм займався в Академії Платона дослідженням конічних перерізів на прикладі макета конуса. Він з'ясував, що задачу про подвоєння куба можна звести до визначення точок перетину двох конічних перерізів. Евклід написав про конічні перерізи чотири книжки, які, однак, донині не збереглись. Найповнішим твором, присвяченим цим кривим, були «Конічні перерізи» Аполлонія із Перги (приблизно 200 до н. е.). Подання конічних перерізів у вигляді рівнянь належить П'єру Ферма та Рене Декарту.

Застосування

Конічні перерізи мають застосування в астрономії: орбіти двох масивних тіл, між якими існує гравітаційна взаємодія, є конічними перерізами, якщо їхній спільний центр мас нерухомий. Якщо вони між собою зв'язані, то рухатимуться по еліптичних орбітах; якщо рухаються окремо, то траєкторії матимуть вигляд парабол або гіпербол (див. закони Кеплера).

Див. також

• Портал «Математика»

• Криві другого порядку.
• Кулі Данделена.
• Коніка дев'яти точок
• Конічна стала
• Проєктивний конус

Джерела

• Синцов Д.М. Аналітична геометрія. — Х.: : Радянська школа, 1931. — 212 с.(укр.)
• Синцов Д.М. Диференціяльна геометрія. — Х.: : Радянська школа, 1931. — 272 с.(укр.)
• Конічні перерізи // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 110. — ISBN 978-966-7407-83-4.
• Анімація на якій зображено різні конічні перерізи^{[недоступне посилання з липня 2019]}.
• Conic Sections [Архівовано 17 жовтня 2008 у Wayback Machine.] — Encyclopaedia of Mathematics.
• Weisstein, Eric W. Конічні перерізи(англ.) на сайті Wolfram MathWorld.[Архівовано 11 грудня 2008 у Wayback Machine.] — Wolfram MathWorld.
• А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, [Архівовано 20 березня 2018 у Wayback Machine.] — М.: МЦНМО, 2007. — 136с.
• И. Н. Бронштейн, Общие свойства конических сечений [Архівовано 28 червня 2006 у Wayback Machine.], Квант, № 5, 1975.