Truncated tetraoctagonal tiling

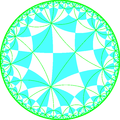
In geometry, the truncated tetraoctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one octagon, and one hexakaidecagon on each vertex. It has Schläfli symbol of tr{8,4}.

Truncated tetraoctagonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.8.16
Schläfli symbol	tr{8,4} or ${\displaystyle t{\begin{Bmatrix}8\\4\end{Bmatrix}}}$
Wythoff symbol	2 8 4 |
Coxeter diagram	or
Symmetry group	[8,4], (*842)
Dual	Order-4-8 kisrhombille tiling
Properties	Vertex-transitive

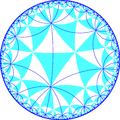
Dual tiling

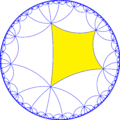
The dual tiling is called an order-4-8 kisrhombille tiling, made as a complete bisection of the order-4 octagonal tiling, here with triangles are shown with alternating colors. This tiling represents the fundamental triangular domains of [8,4] (*842) symmetry.

Symmetry

Truncated tetraoctagonal tiling with *842, , mirror lines

There are 15 subgroups constructed from [8,4] by mirror removal and alternation. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The subgroup index-8 group, [1⁺,8,1⁺,4,1⁺] (4242) is the commutator subgroup of [8,4].

A larger subgroup is constructed as [8,4*], index 8, as [8,4⁺], (4*4) with gyration points removed, becomes (*4444) or (*4⁴), and another [8*,4], index 16 as [8⁺,4], (8*2) with gyration points removed as (*22222222) or (*2⁸). And their direct subgroups [8,4*]⁺, [8*,4]⁺, subgroup indices 16 and 32 respectively, can be given in orbifold notation as (4444) and (22222222).

Small index subgroups of [8,4] (*842)
Index	1	2			4
Diagram
Coxeter	[8,4] =	[1+,8,4] =	[8,4,1+] = =	[8,1+,4] =	[1+,8,4,1+] =	[8+,4+]
Orbifold	*842	*444	*882	*4222	*4242	42×
Semidirect subgroups
Diagram
Coxeter		[8,4+]	[8+,4]	[(8,4,2+)]	[8,1+,4,1+] = = = =	[1+,8,1+,4] = = = =
Orbifold		4*4	8*2	2*42	2*44	4*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[8,4]+ =	[8,4+]+ =	[8+,4]+ =	[8,1+,4]+ =	[8+,4+]+ = [1+,8,1+,4,1+] = = =
Orbifold	842	444	882	4222	4242
Radical subgroups
Index		8	16		32
Diagram
Coxeter		[8,4*] =	[8*,4]	[8,4*]+ =	[8*,4]+
Orbifold		*4444	*22222222	4444	22222222

Related polyhedra and tilings

From a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-4 octagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 7 forms with full [8,4] symmetry, and 7 with subsymmetry.

Uniform octagonal/square tilings v t e
[8,4], (*842) (with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries) (And [(∞,4,∞,4)] (*4242) index 4 subsymmetry)
= = =	=	= = =	=	= =	=
{8,4}	t{8,4}	r{8,4}	2t{8,4}=t{4,8}	2r{8,4}={4,8}	rr{8,4}	tr{8,4}
Uniform duals
V84	V4.16.16	V(4.8)2	V8.8.8	V48	V4.4.4.8	V4.8.16
Alternations
[1+,8,4] (*444)	[8+,4] (8*2)	[8,1+,4] (*4222)	[8,4+] (4*4)	[8,4,1+] (*882)	[(8,4,2+)] (2*42)	[8,4]+ (842)
=	=	=	=	=	=
h{8,4}	s{8,4}	hr{8,4}	s{4,8}	h{4,8}	hrr{8,4}	sr{8,4}
Alternation duals
V(4.4)4	V3.(3.8)2	V(4.4.4)2	V(3.4)3	V88	V4.44	V3.3.4.3.8

*n42 symmetry mutation of omnitruncated tilings: 4.8.2n v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

*nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n v t e
Symmetry *nn2 [n,n]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	*∞∞2 [∞,∞]
Figure
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
Dual
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

See also

• Tilings of regular polygons
• List of uniform planar tilings

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch