Espazo prehilbertiano

En matemáticas, un espazo de produto interno (ou, un espazo prehilbertiano^{[1] [2]}) é un espazo vectorial real ou un espazo vectorial complexo cunha operación chamada produto interno. O produto interno de dous vectores no espazo é un escalar, a miúdo denotado con corchetes angulares como en ${\displaystyle \langle a,b\rangle }$.

Interpretación xeométrica do ángulo entre dous vectores definidos mediante un produto interno

Os espazos de produto escalar, sobre calquera corpo, teñen "produtos escalares" que son simétricos e lineares no primeiro argumento.
Os espazos de produto hermitiano están restrinxidos ao corpo dos números complexos e teñen "produtos hermitianos" que son conxugados-simétricos e lineares no primeiro argumento.
Os espazos de produto interno pódense definir en calquera corpo, tendo "produtos internos" lineares no primeiro argumento, conxugado-simétrico e positivo-definido.
A diferenza dos produtos internos, os produtos escalares e os produtos hermitianos non teñen que ser positivo definidos.

Os produtos internos permiten definicións formais de nocións xeométricas intuitivas, como lonxitudes, ángulos e ortogonalidade (produto interno cero) dos vectores.

Os espazos de produto interno xeneralizan os espazos vectoriais euclidianos, nos que o produto interno é o produto escalar das coordenadas cartesianas.

Os espazos de produto interno de dimensión infinita úsanse amplamente na análise funcional. Ás veces, os espazos de produtos internos sobre o corpo dos números complexos denomínanse espazos unitarios .

O primeiro uso do concepto de espazo vectorial cun produto interno débese a Giuseppe Peano, en 1898.^[3]

Un produto interno induce de xeito natural unha norma asociada, (denotada ${\displaystyle |x|}$ e ${\displaystyle |y|}$ na figura); polo tanto, todo espazo prehilbertiano é un espazo vectorial normado.

Se este espazo normado tamén é completo (é dicir, un espazo de Banach) entón o espazo prehilbertiano é un espazo de Hilbert.^[1]

Se un espazo prehilbertiano H non é un espazo de Hilbert, pódese estender completando a un espazo de Hilbert ${\displaystyle {\overline {H}}.}$ Isto significa que ${\displaystyle H}$ é un subespazo linear de ${\displaystyle {\overline {H}},}$ o produto interno de ${\displaystyle H}$ é a restrición de ${\displaystyle {\overline {H}},}$ e ${\displaystyle H}$ é denso en ${\displaystyle {\overline {H}}}$ para a topoloxía definida pola norma.^{[1] [2]}

Definición

Neste artigo, F denota un corpo que son os números reais ${\displaystyle \mathbb {R} }$ ou os números complexos ${\displaystyle \mathbb {C} .}$ Un escalar é polo tanto un elemento de F. Unha barra sobre unha expresión que representa un escalar indica o complexo conxugado deste escalar. Denotase un vector cero ${\displaystyle \mathbf {0} }$ para distinguilo do escalar 0.

Un espazo de produto interno é un espazo vectorial V sobre o corpo F xunto cun produto interno, é dicir, un mapa

${\displaystyle \langle \cdot ,\cdot \rangle :V\times V\to F}$

que satisfaga as seguintes tres propiedades para todos os vectores ${\displaystyle x,y,z\in V}$ e todos os escalares ${\displaystyle a,b\in F}$.^[4][5]

• Simetría conxugada :

${\displaystyle \langle x,y\rangle ={\overline {\langle y,x\rangle }}.}$

Como ${\textstyle a={\overline {a}}}$ se e só se ${\displaystyle a}$ é real, a simetría conxugada implica que ${\displaystyle \langle x,x\rangle }$ sempre é un número real. Se F é ${\displaystyle \mathbb {R} }$, a simetría conxugada é só simetría.

• Linearidade no primeiro argumento:

${\displaystyle \langle ax+by,z\rangle =a\langle x,z\rangle +b\langle y,z\rangle .}$

• Definición positiva: se ${\displaystyle x}$ non é cero, entón

${\displaystyle \langle x,x\rangle >0}$(a simetría conxugada implica que ${\displaystyle \langle x,x\rangle }$ é real).

Se a condición de definición positiva é substituída por só esixir que ${\displaystyle \langle x,x\rangle \geq 0}$ para tódolos ${\displaystyle x}$, entón obtense a definición de forma hermitiana semidefinida positiva. Unha forma hermitiana semidefinida positiva ${\displaystyle \langle \cdot ,\cdot \rangle }$ é un produto interno se e só se para todos os ${\displaystyle x}$, se ${\displaystyle \langle x,x\rangle =0}$ entón ${\displaystyle x=\mathbf {0} }$.^[6]

Propiedades básicas

Nas seguintes propiedades, que resultan case inmediatamente da definición dun produto interno, x, y e z son vectores arbitrarios, e a e b son escalares arbitrarios.

• ${\displaystyle \langle \mathbf {0} ,x\rangle =\langle x,\mathbf {0} \rangle =0.}$
• ${\displaystyle \langle x,x\rangle }$ é real e non negativo.
• ${\displaystyle \langle x,x\rangle =0}$ se e só se ${\displaystyle x=\mathbf {0} .}$
• ${\displaystyle \langle x,ay+bz\rangle ={\overline {a}}\langle x,y\rangle +{\overline {b}}\langle x,z\rangle .}$
  Isto implica que un produto interno é unha forma sesquilinear.
• ${\displaystyle \langle x+y,x+y\rangle =\langle x,x\rangle +2\operatorname {Re} (\langle x,y\rangle )+\langle y,y\rangle ,}$ onde ${\displaystyle \operatorname {Re} }$ denota a parte real do seu argumento.

Sobre ${\displaystyle \mathbb {R} }$, a simetría conxugada redúcese a simetría e a sesquilinearidade redúcese a bilinearidade. Polo tanto, un produto interno nun espazo vectorial real é unha forma bilinear simétrica definida positivamente. A expansión binomial dun cadrado será logo

${\displaystyle \langle x+y,x+y\rangle =\langle x,x\rangle +2\langle x,y\rangle +\langle y,y\rangle .}$

Notación

Utilízanse varias notacións para os produtos internos, incluíndo ${\displaystyle \langle \cdot ,\cdot \rangle }$, ${\displaystyle \left(\cdot ,\cdot \right)}$, ${\displaystyle \langle \cdot |\cdot \rangle }$ e ${\displaystyle \left(\cdot |\cdot \right)}$, así como o produto habitual con punto.

Exemplos

Números reais e complexos

Entre os exemplos máis sinxelos de espazos de produto interno están ${\displaystyle \mathbb {R} }$ e ${\displaystyle \mathbb {C} .}$ Os números reais ${\displaystyle \mathbb {R} }$ son un espazo vectorial sobre ${\displaystyle \mathbb {R} }$ que se converte nun espazo prehilbertiano coa multiplicación aritmética como produto interno:

${\displaystyle \langle x,y\rangle$ :=xy\quad {\text{ para }}x,y\in \mathbb {R} .}

Os números complexos ${\displaystyle \mathbb {C} }$ son un espazo vectorial sobre ${\displaystyle \mathbb {C} }$ que se converte nun espazo prehilbertiano co produto interno

${\displaystyle \langle x,y\rangle$ :=x{\overline {y}}\quad {\text{ para }}x,y\in \mathbb {C} .}

A diferenza dos números reais, a asignación ${\displaystyle (x,y)\mapsto xy}$ non define un produto interno complexo sobre ${\displaystyle \mathbb {C} .}$

Espazo vectorial euclidiano

Máis xeralmente, o n-espazo real ${\displaystyle \mathbb {R} ^{n}}$ co produto escalar é un espazo prehilbertiano, sendo un exemplo de espazo vectorial euclidiano:${\displaystyle \left\langle {\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}},{\begin{bmatrix}y_{1}\\\vdots \\y_{n}\end{bmatrix}}\right\rangle =x^{\textsf {T}}y=\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+\cdots +x_{n}y_{n},}$ onde ${\displaystyle x^{\operatorname {T} }}$ é a transposta de ${\displaystyle x.}$

Espazo complexo de coordenadas

A forma xeral dun produto interno sobre ${\displaystyle \mathbb {C} ^{n}}$ coñécese como forma hermitiana e vén dada por

${\displaystyle \langle x,y\rangle =y^{\dagger }\mathbf {M} x={\overline {x^{\dagger }\mathbf {M} y}},}$

onde ${\displaystyle M}$ é calquera matriz hermitiana e definida positivamente e ${\displaystyle y^{\dagger }}$ é a transposta conxugada de ${\displaystyle y.}$

Espazo de Hilbert

O artigo sobre os espazos de Hilbert ten varios exemplos de espazos prehilbertianos, nos que a métrica inducida polo produto interno dá un espazo métrico completo.

Un exemplo de espazo prehilbertiano que induce unha métrica incompleta é o espazo ${\displaystyle C([a,b])}$ de funcións con valor complexo continuo ${\displaystyle f}$ e ${\displaystyle g}$ no intervalo ${\displaystyle [a,b].}$ O produto interno é

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(t){\overline {g(t)}}\,\mathrm {d} t.}$

Este espazo non é completo; considere, por exemplo, para o intervalo [ −1, 1 ] a secuencia de funcións en escada continuas, ${\displaystyle \{f_{k}\}_{k},}$ definido por:

${\displaystyle f_{k}(t)={\begin{cases}0&t\in [-1,0]\\1&t\in \left[{\tfrac {1}{k}},1\right]\\kt&t\in \left(0,{\tfrac {1}{k}}\right)\end{cases}}}$

Esta secuencia é unha secuencia de Cauchy para a norma inducida polo produto interno anterior, que non converxe a unha función continua.

Resultados básicos, terminoloxía e definicións

Propiedades da norma

Todo espazo prehilbertiano induce unha norma, chamada norma canónica, que se define por

${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}.}$

Con esta norma, todo espazo prehilbertiano convértese nun espazo vectorial normado.

Daquela, toda propiedade xeral dos espazos vectoriais normados aplícase aos espazos de produto interno. En particular, temos as seguintes propiedades:

• Homoxeneidade absoluta:

${\displaystyle \|ax\|=|a|\,\|x\|}$

para todo ${\displaystyle x\in V}$ e ${\displaystyle a\in F}$

(isto resulta de ${\displaystyle \langle ax,ax\rangle =a{\overline {a}}\langle x,x\rangle }$).

• Desigualdade do triángulo

${\displaystyle \|x+y\|\leq \|x\|+\|y\|}$

para ${\displaystyle x,y\in V.}$

Estas dúas propiedades mostran que temos realmente unha norma.

• Desigualdade de Cauchy-Schwarz

${\displaystyle |\langle x,y\rangle |\leq \|x\|\,\|y\|}$

para cada ${\displaystyle x,y\in V,}$

con igualdade se e só se ${\displaystyle x}$ e ${\displaystyle y}$ son linearmente dependentes.

• Lei do paralelogramo

${\displaystyle \|x+y\|^{2}+\|x-y\|^{2}=2\|x\|^{2}+2\|y\|^{2}}$

para todo ${\displaystyle x,y\in V.}$

A lei do paralelogramo é unha condición necesaria e suficiente para que unha norma sexa definida por un produto interno.

• Identidade de polarización

${\displaystyle \|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}+2\operatorname {Re} \langle x,y\rangle }$

para todo ${\displaystyle x,y\in V.}$

O produto interno pode ser recuperado da norma pola identidade de polarización, xa que a súa parte imaxinaria é a parte real de ${\displaystyle \langle x,iy\rangle .}$

• Desigualdade de Ptolomeo

${\displaystyle \|x-y\|\,\|z\|~+~\|y-z\|\,\|x\|~\geq ~\|x-z\|\,\|y\|}$

para cada ${\displaystyle x,y,z\in V.}$

A desigualdade de Ptolomeo é unha condición necesaria e suficiente para que unha seminorma sexa a norma definida por un produto interno.^[7]

Ortogonalidade

• Ortogonalidade

Dous vectores ${\displaystyle x}$ e ${\displaystyle y}$ dise que son vectores ortogonais, a miúdo escritos ${\displaystyle x\perp y,}$ se o seu produto interno é cero, é dicir, se ${\displaystyle \langle x,y\rangle =0.}$

Para un espazo de produto interno complexo ${\displaystyle H,}$ un operador linear ${\displaystyle T:V\to V}$ é idéntico a ${\displaystyle 0}$ se e só se ${\displaystyle x\perp Tx}$ para todo ${\displaystyle x\in V.}$^[8] Isto non é verdadeiro, en xeral, para espazos de produtos internos reais, xa que é unha consecuencia de que a simetría conxugada é distinta da simetría dos produtos internos complexos. Un contraexemplo nun espazo de produto interno real é ${\displaystyle T}$ unha rotación de 90° en ${\displaystyle \mathbb {R} ^{2}}$, que mapea cada vector a un vector ortogonal pero non é igual a ${\displaystyle 0}$.

• Complemento ortogonal

O complemento ortogonal dun subconxunto ${\displaystyle C\subseteq V}$ é o conxunto ${\displaystyle C^{\bot }}$ dos vectores que son ortogonais a todos os elementos de C; é dicir,

${\displaystyle C^{\bot }:=\{\,y\in V:\langle y,c\rangle =0{\text{ para todo }}c\in C\,\}.}$

Este conxunto ${\displaystyle C^{\bot }}$ é sempre un subespazo vectorial pechado de ${\displaystyle V}$ e se o pechamento ${\displaystyle \operatorname {cl} _{V}C}$ de ${\displaystyle C}$ en ${\displaystyle V}$ é un subespazo vectorial, logo ${\displaystyle \operatorname {cl} _{V}C=\left(C^{\bot }\right)^{\bot }.}$

• Teorema de Pitágoras

Se ${\displaystyle x}$ e ${\displaystyle y}$ son ortogonais, entón

${\displaystyle \|x\|^{2}+\|y\|^{2}=\|x+y\|^{2}.}$

Isto pódese demostrar expresando as normas cadradas en termos de produtos internos, utilizando a aditividade para expandir o lado dereito da ecuación.

O nome Teorema de Pitágoras xorde da interpretación xeométrica en xeometría euclidiana.

• Identidade de Parseval

Unha indución sobre o teorema de Pitágoras produce: se ${\displaystyle x_{1},\ldots ,x_{n}}$ son ortogonais por pares, entón

${\displaystyle \sum _{i=1}^{n}\|x_{i}\|^{2}=\left\|\sum _{i=1}^{n}x_{i}\right\|^{2}.}$

• Ángulo

Cando ${\displaystyle \langle x,y\rangle }$ é un número real, a desigualdade de Cauchy-Schwarz implica que ${\textstyle {\frac {\langle x,y\rangle }{\|x\|\,\|y\|}}\in [-1,1],}$ e así

${\displaystyle \angle (x,y)=\arccos {\frac {\langle x,y\rangle }{\|x\|\,\|y\|}},}$

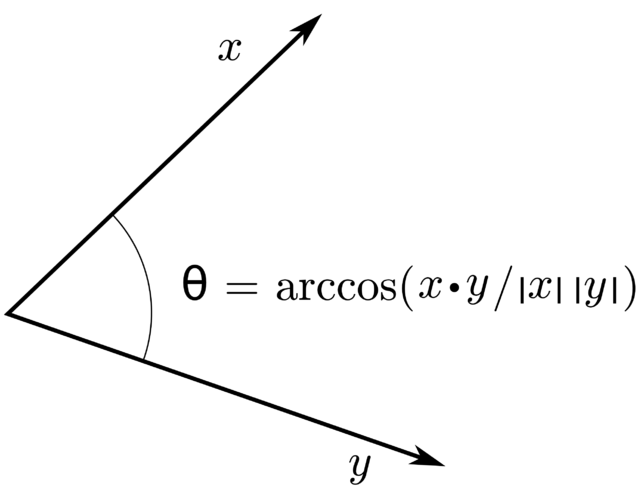
é un número real. Isto permite definir o ángulo (non orientado) de dous vectores nas definicións modernas de xeometría euclidiana en termos de álxebra linear.

A maiores, se ${\displaystyle \langle x,y\rangle }$ é negativo, o ángulo ${\displaystyle \angle (x,y)}$ é maior que 90 graos. Esta propiedade úsase a miúdo en gráficos por ordenador para analizar unha dirección sen ter que avaliar funcións trigonométricas.

Operadores en espazos prehilbertianos

Varios tipos de mapas lineares ${\displaystyle A:V\to W}$ entre os espazos de produto interno ${\displaystyle V}$ e ${\displaystyle W}$ son de relevancia:

• Mapas lineares continuos: ${\displaystyle A:V\to W}$ é linear e continuo en relación á métrica definida anteriormente, ou de forma equivalente, ${\displaystyle A}$ é linear e o conxunto de reais non negativos ${\displaystyle \{\|Ax\|:\|x\|\leq 1\}}$ está limitado, onde ${\displaystyle x}$ oscila sobre a bóla unitaria pechada de ${\displaystyle V}$ está limitada.
• Operadores lineares simétricos: ${\displaystyle A:V\to W}$ é linear e ${\displaystyle \langle Ax,y\rangle =\langle x,Ay\rangle }$ para todos os ${\displaystyle x,y\in V.}$
• Isometrías: ${\displaystyle A:V\to W}$ satisfai ${\displaystyle \|Ax\|=\|x\|}$ para todo ${\displaystyle x\in V.}$ Unha isometría linear (resp. unha isometría antilinear) é unha isometría que tamén é un mapa linear (resp. un mapa antilinear). Para os espazos prehilbertianos, a identidade de polarización pódese usar para mostrar que ${\displaystyle A}$ é unha isometría se e só se ${\displaystyle \langle Ax,Ay\rangle =\langle x,y\rangle }$ para todo ${\displaystyle x,y\in V.}$ Todas as isometrías son inxectivas. O teorema de Mazur-Ulam estabelece que toda isometría sobrexectiva entre dous espazos normados reais é unha transformación afín. En consecuencia, unha isometría ${\displaystyle A}$ entre espazos prehilbertianos reais é un mapa linear se e só se ${\displaystyle A(0)=0.}$ As isometrías son morfismos entre espazos prehilbertianos, e os morfismos de espazos prehilbertianos reais son transformacións ortogonais (comparar coa matriz ortogonal).
• Isomorfismos isométricos: ${\displaystyle A:V\to W}$ é unha isometría que é sobrexectiva (e, polo tanto, bixectiva). Os isomorfismos isométricos tamén se coñecen como operadores unitarios (compárese coa matriz unitaria, matriz na que a súa conxugada transposta é igual que a súa inversa).

Desde o punto de vista da teoría do espazo prehilbertiano, non hai necesidade de distinguir entre dous espazos isométricamente isomorfos. O teorema espectral proporciona unha forma canónica para os operadores normais simétricos, unitarios e máis xeralmente en espazos prehilbertianos de dimensión finita. Unha xeneralización do teorema espectral cúmprese para os operadores normais continuos en espazos de Hilbert.^[9]

Produtos relacionados

O termo "produto interno" oponse ao produto externo (produto tensorial), que é un oposto un pouco máis xeral. Simplemente, en coordenadas, o produto interno é o produto dun covector ${\displaystyle 1\times n}$ cun vector ${\displaystyle n\times 1}$, obtendo unha matriz ${\displaystyle 1\times 1}$ (un escalar), mentres que o produto externo é o produto dun vector ${\displaystyle m\times 1}$ con un covector ${\displaystyle 1\times n}$, produce unha matriz ${\displaystyle m\times n}$.

O produto externo defínese para diferentes dimensións, mentres que o produto interno require a mesma dimensión. Se as dimensións son as mesmas, entón o produto interno é a traza do produto externo (a traza só se define correctamente para matrices cadradas).