トップQs
タイムライン
チャット
視点
カタランの立体
ウィキペディアから
Remove ads
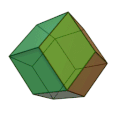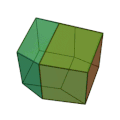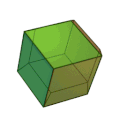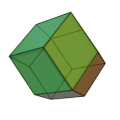
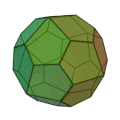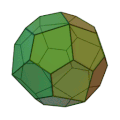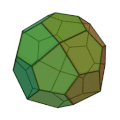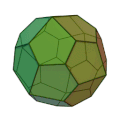
カタランの立体 (Catalan solid) は、半正多面体(アルキメデスの立体)の双対である。アルキメデス双対 (Archimedean dual) とも言う。カタランの立体は13種類存在しており、この数は半正多面体と一致する。[1]

任意の半正多面体に対しen:Dorman Luke constructionを用いることで、その双対となるカタランの立体を得ることができる。 [2]
カタランの立体のいくつかは、ヨハネス・ケプラー (Johannes Kepler) がゾーン多面体の研究の際に発見し、その後1865年にベルギーの数学者ウジェーヌ・カタラン (Eugène Charles Catalan) が13種類の立体を洗い出した。
性質
双対であることから、カタランの立体の面は半正多面体の頂点に、カタランの立体の頂点は半正多面体の面に対応しており[3]、多くの性質は半正多面体と対をなしている。
半正多面体は頂点形状が合同であるため、カタランの立体は面が合同である。逆に半正多面体は2種類以上の面を持つため、カタランの立体の頂点形状は合同ではない。すなわち一様多面体ではない。
半正多面体の辺の長さが等しいことより、カタランの立体は全ての二面角が等しい。
半正多面体が外接球面を持つ一方、カタランの立体は内接球面を持つ。
準正多面体 (quasi-regular polyhedron) の双対にあたる菱形十二面体と菱形三十面体の2つは、元の立体と同様に辺の近傍が合同である。[要出典]
13種類のカタランの立体のうち少なくとも11種類はルパート特性 (Rupert property) を持ち、それ自身のコピーが通り抜けられるような穴を空けることができる。[4]
Remove ads
一覧
Remove ads
脚注
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads