아핀 리 대수

리 대수 이론에서, 아핀 리 대수(affine Lie代數, 영어: affine Lie algebra)는 유한 차원 단순 리 대수 계수를 가진 로랑 다항식 대수에 중심 원소를 더하여 얻는 무한 차원 복소 리 대수다.^{[1][2][3][4][5][6]} 물리학의 등각 장론에서 중요한 역할을 한다. 카츠-무디 대수의 특별한 경우다.

비틀리지 않은 아핀 딘킨 도표들. 새로 추가한 꼭짓점은 녹색이다.

비틀린 아핀 딘킨 도표들.

정의

아핀 리 대수의 개념은 다양한 방법으로 정의될 수 있다.

• 아핀 리 대수는 카츠-무디 대수의 특별한 종류이다.
• 아핀 리 대수는 단순 리 대수 계수의 로랑 다항식의 리 대수의 중심 확대이다.
• 아핀 리 대수는 어떤 특별한 프레셰 리 군의 리 대수(의 복소화의 부분 공간)이다.

이 정의들은 서로 동치이다.

카츠-무디 대수로서의 정의

아핀 리 대수는 카츠-무디 대수 가운데, 카르탕 행렬 ${\displaystyle A}$가 양의 준정부호 행렬이지만 양의 정부호 행렬이 아닌 것들이다. 즉, 만약 아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$가 ${\displaystyle n+1}$개의 단순근을 갖는다면, 그 카르탕 행렬은 ${\displaystyle (n+1)\times (n+1)}$ 정사각 행렬이며 그 계수는 ${\displaystyle l}$이다.

대수적 구성

다음이 주어졌다고 하자.

• 복소수체 위의 유한 차원 이차 리 대수 ${\displaystyle ({\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} },\langle |\rangle \colon {\stackrel {\circ }{\mathfrak {g}}}\otimes _{K}{\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }\to \mathbb {C} )}$. (만약 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$가 반단순 리 대수라면, 이는 킬링 형식으로 잡을 수 있다. 만약 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$가 아벨 리 대수라면, 마찬가지로 적절한 쌍선형 형식을 잡을 수 있다. 만약 둘 다 아니라면, 이는 0으로 놓을 수 있다.)

그렇다면, 아핀 리 대수 ${\displaystyle {\hat {\mathfrak {g}}}^{\mathbb {C} }}$는 ${\displaystyle K}$-벡터 공간으로서 다음과 같다.

${\displaystyle {\hat {\mathfrak {g}}}={\stackrel {\circ }{\mathfrak {g}}}[{\mathsf {z}},{\mathsf {z}}^{-1}]\oplus \mathbb {C} {\mathsf {k}}}$.

즉, ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$의 계수를 가진 로랑 다항식 ${\displaystyle {\mathfrak {g}}^{\mathbb {C} }[{\mathsf {z}},{\mathsf {z}}^{-1}]}$에 중심 확대 ${\displaystyle {\mathsf {k}}}$를 더한 것이다. 물리학적으로 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }[{\mathsf {z}},{\mathsf {z}}^{-1}]}$는 대칭의 보존류들을 나타내고, ${\displaystyle {\mathsf {k}}}$는 대칭의 변칙을 나타낸다.

${\displaystyle {\hat {\mathfrak {g}}}^{\mathbb {C} }}$ 위에는 다음과 같은 리 괄호를 정의한다. ${\displaystyle a,b\in {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$라고 하면,

${\displaystyle [a{\mathsf {z}}^{m},b{\mathsf {z}}^{n}]=[a,b]{\mathsf {z}}^{m+n}+\delta _{m+n,0}m\langle a|b\rangle {\mathsf {k}}}$

${\displaystyle [{\mathsf {k}},a{\mathsf {z}}^{n}]=[{\mathsf {k}},{\mathsf {k}}]=0}$

${\displaystyle {\mathsf {k}}}$는 중심 원소이므로, 리 대수의 짧은 완전열

${\displaystyle 0\to \mathbb {C} {\mathsf {k}}\to {\hat {\mathfrak {g}}}^{\mathbb {C} }\to {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }\otimes \mathbb {C} [{\mathsf {z}},{\mathsf {z}}^{-1}]\to 0}$

이 존재한다.

형식적 변수 ${\displaystyle {\mathsf {z}}}$ 대신, ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 정규 직교 기저 ${\displaystyle g^{a}}$를 잡아, 직접

${\displaystyle g_{m}^{a}=g^{a}{\mathsf {z}}^{m}}$

를 적을 수 있다. 이 경우 리 괄호는 다음과 같다.

${\displaystyle [g_{m}^{a},g_{n}^{b}]=f^{ab}{}_{c}g_{m+n}^{c}+\delta _{m+n,0}m\delta ^{ab}{\mathsf {k}}}$

${\displaystyle [{\mathsf {k}},g_{m}^{a}]=0}$

여기서 ${\displaystyle f^{ab}{}_{c}}$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 구조 상수이다.

실수 형태

${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$가 실수 이차 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {R} }}$의 복소화라고 하자. 그렇다면, 복소수 아핀 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$는 실수 리 대수로서 다음과 같은 자기 동형을 갖는다.

${\displaystyle {\mathsf {z}}\mapsto {\mathsf {z}}^{-1}}$

${\displaystyle \mathrm {i} \mapsto -\mathrm {i} }$

${\displaystyle {\mathsf {k}}\mapsto {\mathsf {k}}}$

${\displaystyle x\mapsto x\qquad \forall x\in {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {R} }}$

즉, 이는 두 복소수 벡터 공간 사이의 반선형(영어: antilinear) 사상이다. 이 반선형 사상의 고정점

${\displaystyle {\hat {\mathfrak {g}}}^{\mathbb {R} }={\stackrel {\circ }{\mathfrak {g}}}\otimes _{\mathbb {R} }\mathbb {R} [z+z^{-1},\mathrm {i} (z-z^{-1})]+\mathbb {R} {\mathsf {k}}}$

은 실수 리 대수를 이룬다.

미분 연산의 추가

복소수 벡터 공간

${\displaystyle {\tilde {\mathfrak {g}}}^{\mathbb {C} }={\hat {\mathfrak {g}}}^{\mathbb {C} }\oplus \mathbb {C} {\mathsf {d}}}$

위에 다음과 같은 리 괄호를 정의할 수 있다.

${\displaystyle [{\mathsf {d}},az^{m}]=-\mathrm {i} ma{\mathsf {z}}^{m}\qquad \forall a\in {\stackrel {\circ }{\mathfrak {g}}}^{\mathbb {C} }}$

${\displaystyle [{\mathsf {d}},{\mathsf {c}}]=0}$

즉,

${\displaystyle [{\mathsf {d}},-]=-\mathrm {i} {\mathsf {z}}{\frac {\mathrm {d} }{\mathrm {d} {\mathsf {z}}}}}$

이다. 만약 형식적으로 ${\displaystyle {\mathsf {z}}=\exp(\mathrm {i} {\mathsf {t}})}$로 놓는다면,

${\displaystyle [{\mathsf {d}},-]={\frac {\mathrm {d} }{\mathrm {d} {\mathsf {t}}}}}$

가 된다.

또한,

${\displaystyle [{\mathsf {d}},a(z+z^{-1})]=-a\mathrm {i} (z-{\mathsf {z}}^{-1})}$

${\displaystyle [{\mathsf {d}},\mathrm {i} a(z-z^{-1})]=a(z+{\mathsf {z}}^{-1})}$

이므로, 이 미분 연산은 실수 형태 ${\displaystyle {\hat {\mathfrak {g}}}^{\mathbb {R} }}$에도 잘 정의된다.

뒤틀린 아핀 리 대수

${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}[{\mathsf {z}},{\mathsf {z}}^{-1}]}$를 원 위의 푸리에 급수로 해석할 수 있다. 즉, ${\displaystyle z=\exp(\mathrm {i} {\mathsf {t}})}$로 놓으면, ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}[{\mathsf {z}},{\mathsf {z}}^{-1}]}$를 주기적 함수 ${\displaystyle \mathbb {S} ^{1}\to {\stackrel {\circ }{\mathfrak {g}}}}$로 해석할 수 있다. 즉, ${\displaystyle a(0)=a(2\pi )}$의 주기적 경계 조건을 놓은 경우다.

만약 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$가 자명하지 않은 자기 동형 ${\displaystyle \sigma \in \operatorname {Aut} ({\stackrel {\circ }{\mathfrak {g}}})}$를 가진다면, 다음과 같은 경계 조건을 생각할 수 있다.

${\displaystyle \sigma a(0)=a(2\pi )}$.

이와 같은 경우를 뒤틀린 아핀 리 대수(twisted affine Lie algebra)라고 한다. 마찬가지로 뒤틀린 카츠-무디 대수(twisted Kač–Moody algebra)를 정의할 수 있다.

아핀 리 대수의 기하학적 정의

아핀 리 대수는 기하학적으로 리 대수 값의 주기 함수를 통해 구성될 수 있다.^{[3]:824, §4.1}

구체적으로, 킬링 형식이 음의 정부호인 실수 단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$가 주어졌다고 하자. 그렇다면, 실수 프레셰 공간

${\displaystyle \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}={\mathcal {C}}^{\infty }(\mathbb {S} ^{1},{\stackrel {\circ }{\mathfrak {g}}})}$

을 정의할 수 있다. 이는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$값의 매끄러운 주기 함수로 구성된다. 그 위의 실수 벡터 공간 구조는 점별 덧셈이며, 점별 리 괄호를 부여하면 이는 리 대수를 이룬다. 그 복소화는 (푸리에 급수로서) 다음과 같은 부분 벡터 공간을 갖는다.

${\displaystyle \iota \colon \mathbb {C} [{\mathsf {z}},{\mathsf {z}}^{-1}]\otimes _{\mathbb {R} }{\stackrel {\circ }{\mathfrak {g}}}\subseteq \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}\otimes _{\mathbb {R} }\mathbb {C} }$

${\displaystyle \iota ({\mathsf {z}}^{n}\otimes x)\colon t\mapsto \exp(\mathrm {i} tn)x\qquad (x\in {\mathfrak {g}},\;t\in \mathbb {R} /2\pi \mathbb {Z} =\mathbb {S} ^{1})}$

이 경우, 우변을 좌변의 (프레셰 공간으로의) 완비화로 여길 수 있다. 실수 계수로는, 이는

${\displaystyle \iota _{\mathbb {R} }\colon \mathbb {R} [{\mathsf {z}}+{\mathsf {z}}^{-1},\mathrm {i} ({\mathsf {z}}-{\mathsf {z}}^{-1})]\otimes _{\mathbb {R} }{\stackrel {\circ }{\mathfrak {g}}}\to \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}}$

이다.

고리 리 대수 ${\displaystyle \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}}$의 리 대수 코호몰로지에서, 다음과 같은 2차 공사슬이 존재한다.

${\displaystyle \alpha \colon \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}\times \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}\to \mathbb {R} }$

${\displaystyle \alpha \colon (x,y)\mapsto {\frac {\delta ^{2}}{2\pi }}\int _{\mathbb {S} ^{1}}\langle x(t)|y(t)\rangle \,\mathrm {d} t}$

여기서

• ${\displaystyle \langle -|-\rangle }$은 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$ 위의 어떤 임의의 불변 비퇴화 이차 형식이다. (이는 킬링 형식의 스칼라배이다.) 비퇴화성으로 인하여, 이는 쌍대 공간 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}^{*}}$ 위의 비퇴화 이차 형식으로도 여길 수 있다.
• ${\displaystyle \delta ^{2}}$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 근계의 가장 긴 근의 제곱 노름이다. 여기서 제곱 노름은 ${\displaystyle \langle -|-\rangle }$에 따른 것이다.
• ${\displaystyle \mathbb {S} ^{1}}$의 측도 ${\displaystyle \mathrm {d} t}$에 따르면, ${\displaystyle \textstyle \int _{\mathbb {S} ^{1}}\mathrm {d} t=2\pi }$이다.

이 2차 공사슬은 리 대수의 짧은 완전열

${\displaystyle 0\to \mathbb {R} \to {\bar {\mathfrak {g}}}\to \mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}\to 0}$

을 정의한다. 이 경우, ${\displaystyle {\mathfrak {g}}}$에 대응하는 뒤틀리지 않은 아핀 리 대수 ${\displaystyle {\hat {\mathfrak {g}}}}$는 자연스럽게 다음과 같이 ${\displaystyle {\bar {\mathfrak {g}}}}$의 부분 리 대수가 된다.

${\displaystyle {\begin{matrix}0&\to &\mathbb {R} &\to &{\hat {\mathfrak {g}}}&\to &{\stackrel {\circ }{\mathfrak {g}}}\otimes _{\mathbb {R} }\mathbb {R} [z+z^{-1},\mathrm {i} (z-z^{-1})]&\to &0\\&&\downarrow &&\downarrow &&\downarrow \\0&\to &\mathbb {R} &\to &{\bar {\mathfrak {g}}}&\to &\mathrm {L} {\stackrel {\circ }{\mathfrak {g}}}&\to &0\end{matrix}}}$

리 군의 기하학적 정의

실수 계수 아핀 리 대수의 프레셰 공간 완비화는 어떤 프레셰 다양체인 리 군의 리 대수이다.^{[3]:825, §4.1}

구체적으로, 단일 연결 콤팩트 단순 리 군 ${\displaystyle {\stackrel {\circ }{G}}}$와 그 실수 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$가 주어졌다고 하자. 그렇다면, 다음과 같은 고리군을 정의할 수 있다.

${\displaystyle \mathrm {L} {\stackrel {\circ }{G}}={\mathcal {C}}^{\infty }(\mathbb {S} ^{1},{\stackrel {\circ }{G}})}$

즉, 이는 ${\displaystyle {\stackrel {\circ }{G}}}$값의 매끄러운 주기 함수의 공간이다. 이는 프레셰 다양체를 이루며, 점별 곱셈을 통하여 위상군을 이룬다.

아핀 리 대수는 ${\displaystyle \mathbb {R} [{\mathsf {z}}+{\mathsf {z}}^{-1},\mathrm {i} ({\mathsf {z}}-{\mathsf {z}}^{-1})]\otimes _{\mathbb {R} }{\stackrel {\circ }{\mathfrak {g}}}}$의 중심 확대이다. 위상군으로서, 이는 짧은 완전열

${\displaystyle 1\to \operatorname {U} (1)\to {\hat {G}}\to \mathrm {L} {\stackrel {\circ }{G}}\to 1}$

에 해당한다. 위상수학적으로, 이는 U(1) 주다발을 이룬다.

구체적으로, 원판 ${\displaystyle \mathbb {D} ^{2}}$를 생각하자. 이제,

${\displaystyle \mathrm {L} {\stackrel {\circ }{G}}=G_{\mathbb {D} ^{2}}/{\mathcal {G}}}$

${\displaystyle G_{\mathbb {D} ^{2}}={\mathcal {C}}^{\infty }(\mathbb {D} ^{2},G)}$

${\displaystyle {\mathcal {G}}=\{\alpha \in G_{\mathbb {D} ^{2}}\colon \alpha \upharpoonright \partial \mathbb {D} ^{2}=1_{\stackrel {\circ }{G}}\}\cong {\mathcal {C}}_{\bullet }^{\infty }(\mathbb {S} ^{2},{\stackrel {\circ }{G}})}$

이다. 여기서 ${\displaystyle {\mathcal {G}}}$는 일종의 게이지 변환군으로 여길 수 있다. 이제, ${\displaystyle G_{\mathbb {D} ^{2}}}$ 위의 다음과 같은 함수를 생각하자.

${\displaystyle \gamma \colon G_{\mathbb {D} ^{2}}\times G_{\mathbb {D} ^{2}}\to \mathbb {R} }$

${\displaystyle \gamma (g,h)={\frac {1}{4\pi \delta ^{2}}}\int _{\mathbb {D} ^{2}}\langle g^{-1}\mathrm {d} g|h^{-1}\mathrm {d} h\rangle }$

여기서

• ${\displaystyle \langle -|-\rangle }$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$ 위의 불변 비퇴화 이차 형식이며, (예를 들어) 딸림표현에서의 대각합 ${\displaystyle \langle x,y\rangle =\operatorname {tr} (xy)}$으로 여길 수 있다.
• ${\displaystyle \delta ^{2}}$는 ${\displaystyle \langle -|-\rangle }$에 따른, ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 근계의 가장 긴 근의 제곱 노름이다.

그렇다면,

${\displaystyle \exp(\mathrm {i} l\gamma (-,-))\colon G_{\mathbb {D} ^{2}}\times G_{\mathbb {D} ^{2}}\to \mathbb {C} \qquad (l\in \mathbb {Z} )}$

는 (자명한 계수의) ${\displaystyle {\mathcal {C}}^{\infty }(\mathbb {D} ^{2},G)}$의 군 코호몰로지의 2차 공사슬을 이루며, 이는 ${\displaystyle G_{\mathbb {D} ^{2}}}$의 중심 확대

${\displaystyle 1\to \operatorname {U} (1)\to {\hat {G}}_{\mathbb {D} ^{2}}\to G_{\mathbb {D} ^{2}}\to 1}$

를 정의한다.

이제, 임의의 ${\displaystyle \alpha \in {\mathcal {G}}}$에 대하여,

${\displaystyle \iota _{l}\colon {\mathcal {G}}\to {\hat {G}}_{\mathbb {D} ^{2}}}$

${\displaystyle \iota _{l}\colon \alpha \mapsto \left(\alpha ,\exp \left({\frac {\mathrm {i} l}{12\pi \delta ^{2}}}\int _{\mathbb {D} ^{3}}\operatorname {tr} ({\bar {\alpha }}^{-1}\mathrm {d} {\bar {\alpha }})^{3}\right)\right)}$

를 정의할 수 있다. 여기서

${\displaystyle {\bar {\alpha }}\colon \mathbb {D} ^{3}\to {\stackrel {\circ }{G}}}$

${\displaystyle ({\bar {\alpha }}\upharpoonright \partial \mathbb {D} ^{3})=\alpha }$

는 ${\displaystyle \alpha \colon \mathbb {S} ^{2}\to {\stackrel {\circ }{G}}}$의, 3차원 공 ${\displaystyle \mathbb {D} ^{3}}$으로의 임의의 확장이다. 이 경우, 위 표현이 ${\displaystyle {\bar {\alpha }}}$의 선택에 의존하지 않음을 보일 수 있다. 이 사상은 사실상 베스-추미노-위튼 모형의 작용의 항에 해당한다.

이 사상은 단사 함수이자 군 준동형이며, ${\displaystyle \iota _{l}({\mathcal {G}})}$는 ${\displaystyle {\hat {G}}_{\mathbb {D} ^{2}}}$의 정규 부분군이다. 따라서, 몫군

${\displaystyle {\hat {G}}_{l}={\frac {{\hat {G}}_{\mathbb {D} ^{2}}}{\iota _{l}({\mathcal {G}})}}}$

을 정의할 수 있다. 이는 짧은 완전열

${\displaystyle 1\to \operatorname {U} (1)\to {\hat {G}}_{l}\to \mathrm {L} G\to 1}$

을 구성한다. (정수 ${\displaystyle l\in \mathbb {Z} }$은 ${\displaystyle {\hat {\mathfrak {g}}}}$의 표현의 준위에 해당한다.) 정의에 따라, ${\displaystyle {\hat {G}}_{l}}$의 리 대수는 (${\displaystyle l\neq 0}$일 경우, ${\displaystyle l}$의 값에 상관없이) ${\displaystyle {\hat {\mathfrak {g}}}}$이다.

성질

아핀 리 대수는 항상 대칭화 가능 카츠-무디 대수이다. 카르탕 행렬의 대칭 성분은 중복수 1의 고윳값 0을 가지며, 나머지 고윳값들은 모두 양수이다. 따라서, 아핀 리 대수의 카르탕 행렬식은 항상 0이다. 카르탕 행렬의 대칭 성분의 나머지 고윳값들은 그 기본 단순 리 대수의 것들과 같다.

콕서터 수와 쌍대 콕서터 수

아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 단순근들이 ${\displaystyle \alpha _{0},\dots ,\alpha _{n}}$이며, 단순 쌍대근들이 ${\displaystyle \alpha _{0}^{\vee },\dots ,\alpha _{n}^{\vee }}$라고 하자. 콕서터 라벨(영어: Coxeter label) ${\displaystyle a_{i}}$와 쌍대 콕서터 라벨(영어: dual Coxeter label) ${\displaystyle a_{i}^{\vee }}$는 카르탕 행렬 ${\displaystyle A}$에 대하여

${\displaystyle 0=a^{\top }A=Aa^{\vee }}$

를 만족시키는 벡터이다.^{[2]:96, (2.1.16)} 이 경우, ${\displaystyle a}$ 및 ${\displaystyle a^{\vee }}$의 모든 성분들이 양의 정수이며 최대 공약수가 1이게 정의한다.

아핀 리 대수의 콕서터 수(영어: Coxeter number) ${\displaystyle h}$와 쌍대 콕서터 수(영어: dual Coxeter number) ${\displaystyle h^{\vee }}$는 각각 (쌍대) 콕서터 라벨의 성분들의 합이다.

${\displaystyle {\mathsf {h}}({\mathfrak {g}})=\sum _{i=0}^{n}a_{i}}$

${\displaystyle {\mathsf {h}}^{\vee }({\mathfrak {g}})=\sum _{i=0}^{n}a_{i}^{\vee }}$

아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 표준 중심 원소(標準中心元素, 영어: canonical central element) ${\displaystyle k\in {\mathfrak {h}}}$는 다음과 같이 정의되는, 카르탕 부분 대수 ${\displaystyle {\mathfrak {h}}\subseteq {\mathfrak {g}}}$의 원소이다.

${\displaystyle k=\sum _{i=0}^{n}a_{i}^{\vee }\alpha _{i}^{\vee }}$

그렇다면, ${\displaystyle {\mathfrak {g}}}$의 중심은 1차원 부분 대수

${\displaystyle \operatorname {Z} ({\mathfrak {g}})=\mathbb {C} {\mathsf {k}}}$

이다. 마찬가지로,

${\displaystyle \delta =\sum _{i=0}^{n}a_{i}\alpha _{i}}$

를 정의하자.

근계의 구조

아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 기본 단순 리 대수가 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$라고 하자. ${\displaystyle r}$가 아핀 리 대수를 구성할 때 사용한 자기 동형의 차수라고 하자. 예를 들어, ${\displaystyle {\tilde {D}}_{4}^{(3)}}$의 경우, ${\displaystyle r=3}$이다. 그렇다면, ${\displaystyle {\mathfrak {g}}}$의 실근들의 집합 ${\displaystyle \Delta ^{\text{re}}({\mathfrak {g}})}$는 구체적으로 다음과 같다.^{[1]:83, Proposition 6.3a,b,c}

${\displaystyle \Delta ^{\text{re}}({\mathfrak {g}})={\begin{cases}{\stackrel {\circ }{\Delta }}+\mathbb {Z} \delta &r=1\\({\stackrel {\circ }{\Delta }}_{\text{short}}+\mathbb {Z} \delta )\cup ({\stackrel {\circ }{\Delta }}_{\text{long}}+r\mathbb {Z} \delta )&r\in \{2,3\},\;{\mathfrak {g}}\not \cong A_{2n}^{(2)}\\{\frac {1}{2}}\left({\stackrel {\circ }{\Delta }}_{\text{long}}+(2\mathbb {Z} -1)\delta \right)\cup \left({\stackrel {\circ }{\Delta }}_{\text{short}}+\mathbb {Z} \delta \right)\cup \left({\stackrel {\circ }{\Delta }}_{\text{long}}+2\mathbb {Z} \delta \right)&{\mathfrak {g}}\cong A_{2n}^{(2)}\end{cases}}}$

${\displaystyle {\mathfrak {g}}}$의 허근들의 집합 ${\displaystyle \Delta ^{\text{im}}({\mathfrak {g}})}$는 다음과 같다.^{[1]:64, Theorem 5.6b}

${\displaystyle \Delta ^{\text{im}}({\mathfrak {g}})=(\mathbb {Z} \setminus \{0\})\delta }$

(영벡터는 정의에 따라 근이 아니다.) 또한, ${\displaystyle \delta }$는 항상 양근이다. 즉, 양의 허근들의 집합은 다음과 같다.^{[1]:64, Theorem 5.6b}

${\displaystyle \Delta ^{{\text{im}},+}({\mathfrak {g}})=\mathbb {Z} ^{+}\delta }$

기본 단순 리 대수

단순근들의 순서를 임의로 잡았을 때, ${\displaystyle {\mathfrak {g}}}$의 축척 원소(영어: scaling element) ${\displaystyle d\in {\mathfrak {h}}}$는 다음 성질을 만족시키는, 카르탕 부분 대수의 원소이다.

${\displaystyle \langle \alpha _{i},d\rangle =\delta _{i,0}}$

축척 원소를 선택하였다면, ${\displaystyle {\mathfrak {g}}}$와 그 카르탕 부분 대수 ${\displaystyle {\mathfrak {h}}\subseteq {\mathfrak {g}}}$는 다음과 같은 구체적인 기저로 나타낼 수 있다.

${\displaystyle {\mathfrak {g}}=[{\mathfrak {g}},{\mathfrak {g}}]\oplus \mathbb {C} {\mathsf {d}}}$

${\displaystyle {\mathfrak {h}}=\operatorname {Span} \{\alpha _{0}^{\vee },\dots ,\alpha _{r}^{\vee },d\}}$

${\displaystyle {\mathfrak {h}}}$에서, ${\displaystyle k}$ 및 ${\displaystyle d}$에 수직이 되는 부분 공간을 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}}$라고 하자.

${\displaystyle {\mathfrak {h}}={\stackrel {\circ }{\mathfrak {h}}}\oplus \mathbb {C} {\mathsf {k}}\oplus \mathbb {C} {\mathsf {d}}}$

아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 슈발레 생성원을

${\displaystyle (e_{0},f_{0}),\dots ,(e_{n},f_{n})}$

이라고 하자. 그렇다면, 아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 기본 단순 리 대수(영어: underlying simple Lie algebra) ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}\subsetneq {\mathfrak {g}}}$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}}$ 및 ${\displaystyle (e_{1},f_{1}),\dots ,(e_{n},f_{n})}$로 생성되는 리 부분 대수이다. 이는 항상 유한 차원 단순 리 대수이며, 기본 단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 카르탕 부분 대수는 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}}$이며, 그 근계 및 쌍대 근계는

${\displaystyle {\stackrel {\circ }{\Delta }}=\Delta \cap {\stackrel {\circ }{\mathfrak {h}}}^{*}}$

${\displaystyle {\stackrel {\circ }{\Delta }}^{\vee }=\Delta ^{\vee }\cap {\stackrel {\circ }{\mathfrak {h}}}}$

이며, 그 단순근 및 단순 쌍대근들은 각각

${\displaystyle \{\alpha _{1},\dots ,\alpha _{n}\}}$

${\displaystyle \{\alpha _{1}^{\vee },\dots ,\alpha _{n}^{\vee }\}}$

이다.

바일 군

아핀 리 대수 ${\displaystyle {\mathfrak {g}}}$의 바일 군 ${\displaystyle \operatorname {Weyl} ({\mathfrak {g}})}$은 아핀 콕서터 군이며, 그 기본 단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 바일 군 ${\displaystyle \operatorname {Weyl} ({\stackrel {\circ }{\mathfrak {g}}})}$과 어떤 자유 아벨 군의 반직접곱이다.^{[1]:88, Proposition 6.5}

${\displaystyle \operatorname {Weyl} ({\mathfrak {g}})=\operatorname {Weyl} ({\stackrel {\circ }{\mathfrak {g}}})\rtimes M}$

여기서

${\displaystyle M={\begin{cases}\operatorname {Span} _{\mathbb {Z} }{\stackrel {\circ }{\Delta }}&r=1\\\operatorname {Span} _{\mathbb {Z} }{\stackrel {\circ }{\Delta }}^{\vee }&r\in \{2,3\}\end{cases}}}$

는 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}}$ 속의 격자(의 병진 이동군)이다. 여기서, 단순 리 대수의 근계에 주어진 내적을 사용하여 동형 ${\displaystyle \circ {\mathfrak {h}}\cong \circ {\mathfrak {h}}^{*}}$를 암묵적으로 사용하였다.

표현론

${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 유한 차원 유니터리 표현

${\displaystyle {\stackrel {\circ }{\rho }}\colon {\mathfrak {g}}\to {\mathfrak {u}}(n)}$

이 주어졌으며, 자연수 ${\displaystyle k\in \mathbb {N} }$가 주어졌다고 하자. 그렇다면, 아핀 리 대수 ${\displaystyle {\hat {\mathfrak {g}}}}$에서, 포함 관계 ${\displaystyle \iota \colon {\stackrel {\circ }{\mathfrak {g}}}\to {\hat {\mathfrak {g}}}}$에 대하여

${\displaystyle {\stackrel {\circ }{\rho }}=\rho \circ \iota }$

이며

${\displaystyle \rho ({\mathsf {k}})=k}$

가 되는, 무한 차원 분해 가능 복소수 힐베르트 공간으로 가는 기약 표현

${\displaystyle \rho \colon {\hat {\mathfrak {g}}}\to {\mathcal {L}}({\mathcal {H}},{\mathcal {H}})}$

이 유일하게 존재한다.

스가와라 구성

단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$에 대응되는 (뒤틀리지 않은) 복소수 아핀 리 대수 ${\displaystyle {\hat {\mathfrak {g}}}=\mathbb {g} [{\mathsf {z}},{\mathsf {z}}^{-1}]\oplus \mathbb {C} {\mathsf {c}}}$의 표현 ${\displaystyle V}$가 주어졌다고 하자.

이 경우, ${\displaystyle V}$에 다음과 같은 비라소로 대수의 표현이 존재한다.

${\displaystyle {\mathsf {L}}_{n}={\frac {1}{{\mathsf {k}}+{\mathsf {h}}^{\vee }({\mathfrak {g}})}}\sum _{m\in \mathbb {Z} }\eta _{ab}(x^{a}{\mathsf {z}}^{m})(x^{b}{\mathsf {z}}^{-m})\qquad (n\neq 0)}$

${\displaystyle {\mathsf {L}}_{0}={\frac {2}{{\mathsf {k}}+{\mathsf {h}}^{\vee }({\mathfrak {g}})}}\sum _{m=0}^{\infty }\eta _{ab}(x^{a}{\mathsf {z}}^{m})(x^{b}{\mathsf {z}}^{-m})}$

${\displaystyle {\mathsf {c}}={\frac {{\mathsf {k}}\dim {\stackrel {\circ }{\mathfrak {g}}}}{{\mathsf {k}}+{\mathsf {h}}^{\vee }({\stackrel {\circ }{\mathfrak {g}}})}}}$

이를 스가와라 구성([菅原]構成, 영어: Sugawara construction)이라고 한다.^{[7][8]:(4.15), §4.2} 여기서

• ${\displaystyle {\mathsf {h}}^{\vee }({\stackrel {\circ }{\mathfrak {g}}})}$는 단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 이중 콕서터 수이다.
• ${\displaystyle \eta _{ab}}$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 킬링 형식의 스칼라배이며, 이 비퇴화 이차 형식에 따라서 ${\displaystyle {\mathfrak {g}}}$의 근 가운데 가장 긴 것의 제곱 길이가 2이다. (만약 짧은 근이 존재한다면, 그 제곱 길이는 1이 된다.)
• ${\displaystyle {\mathsf {k}}}$는 중심 원소이므로, 기약 표현에서 그 값은 상수이다. 따라서 단순히 수로 취급할 수 있다.
• 합이 무한해 보이지만, 이들이 사다리 연산자로 작용하므로, 실제로는 각 베르마 가군에서 적절한 기저에서 각 기저 벡터의 경우 오직 유한 개의 항만이 작용하게 된다.
• ${\displaystyle {\mathsf {L}}_{0}}$의 정의가 특별한 것은 표준 순서를 가했기 때문이다.

보다 일반적으로, 반단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}}$의 표현 ${\displaystyle V}$ 및 부분 단순 리 대수 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}\subseteq {\stackrel {\circ }{\mathfrak {g}}}}$가 주어졌다고 하자. 그렇다면, ${\displaystyle {\hat {\mathfrak {g}}}}$에 대응하는 스가와라 구성

${\displaystyle ({\mathsf {L}}'_{n},{\mathsf {c}}')_{\mathbb {Z} }}$

및 ${\displaystyle {\hat {\mathfrak {h}}}}$에 대응하는 스가와라 구성

${\displaystyle ({\mathsf {L}}''_{n},{\mathsf {c}}'')_{\mathbb {Z} }}$

이 주어진다. 이 경우,

${\displaystyle {\mathsf {L}}_{n}={\mathsf {L}}'_{n}-{\mathsf {L}}''_{n}}$

${\displaystyle {\mathsf {c}}={\mathsf {c}}'-{\mathsf {c}}''={\frac {{\mathsf {k}}\dim {\stackrel {\circ }{\mathfrak {g}}}}{{\mathsf {k}}+{\mathsf {h}}^{\vee }({\stackrel {\circ }{\mathfrak {g}}})}}-{\frac {{\mathsf {k}}\dim {\stackrel {\circ }{\mathfrak {h}}}}{{\mathsf {k}}+{\mathsf {h}}^{\vee }({\stackrel {\circ }{\mathfrak {h}}})}}}$

를 정의하면, 이는 비라소로 대수의 유니터리 표현을 이룬다.^[9] 이를 공액류 구성(영어: coset construction) 또는 고더드-켄트-올리브 구성(영어: Goddard–Kent–Olive construction) 또는 GKO 구성(영어: GKO construction)이라고 한다.

이를 통하여 비라소로 대수의 모든 ${\displaystyle c<1}$ 유니터리 표현을 구현할 수 있다. 구체적으로, ${\displaystyle c=1-6/(k+2)(k+3)}$ 유니터리 표현을 구현하려면,

${\displaystyle {\hat {\mathfrak {g}}}={\widehat {\mathfrak {su}}}(2)_{k}\times {\widehat {\mathfrak {su}}}(2)_{1}}$

${\displaystyle {\hat {\mathfrak {h}}}={\widehat {\mathfrak {su}}}(2)_{k+1}}$

를 취하면 된다. 여기서 ${\displaystyle {\stackrel {\circ }{\mathfrak {h}}}={\mathfrak {su}}(2)}$는 ${\displaystyle {\stackrel {\circ }{\mathfrak {g}}}={\mathfrak {su}}(2)\oplus {\mathfrak {su}}(2)}$의 대각 성분이다. 이 경우

${\displaystyle \dim {\mathfrak {su}}(2)=3}$

${\displaystyle {\mathsf {h}}^{\vee }({\mathfrak {su}}(2))=2}$

이므로,

${\displaystyle {\mathsf {c}}={\frac {3k}{k+2}}+{\frac {3\times 1}{1+2}}-{\frac {3(k+1)}{k+3}}=1-{\frac {6}{(k+2)(k+3)}}}$

임을 계산할 수 있다.

분류

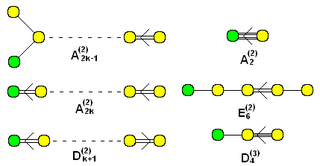
단순 아핀 리 대수들 및 그 딘킨 도표들은 다음과 같다. 아래 표에서, "긴 실근의 동치류 수"는 근 ${\displaystyle \Delta }$에서, ${\displaystyle \delta }$를 더한 것을 무시한 동치류들의 수 가운 데, 긴 근 및 짧은 근들의 수이다. (${\displaystyle {\tilde {A}}_{2n}^{(2)}}$의 경우 근의 길이가 세 종류가 있으며, 이 경우 중간 길이 및 가장 짧은 길이의 근들의 수를 "짧은 근"에 표기하였다.) 이 경우 긴 근의 길이는 항상 ${\displaystyle {\sqrt {2}}}$로 규격화하였고, 짧은 근의 길이는 이에 비례하여 측정하였다.

딘킨 그림에서, 4중 화살표 (즉, 카르탕 행렬에서 ${\displaystyle A_{ij}A_{ji}=4}$인 경우)는 ${\displaystyle {\xrightarrow {4}}}$ 및 ${\displaystyle {\stackrel {4}{\leftrightarrow }}}$로 표기하였다. 이 경우 ${\displaystyle A_{ij}=A_{ji}=-2}$인 경우는 ${\displaystyle {\stackrel {4}{\leftrightarrow }}}$이며, ${\displaystyle A_{ij}=-1,\;A_{ji}=-4}$인 경우는 ${\displaystyle {\xrightarrow {4}}}$이다.

기호 [1]:53–55	타 기호 [10]:24	타 기호 [11]:6–12	타 기호 [2]:94–95	바일 군 궤도 수	긴 실근의 동치류 수	짧은 실근의 동치류 수	딘킨 도표	콕서터 라벨 [2]:94–95	쌍대 콕서터 라벨 [2]:94–95[10]:24–25	콕서터 수[1]:80	쌍대 콕서터 수[1]:80
${\displaystyle {\tilde {A}}_{1}}$	${\displaystyle A_{1}^{u}=A_{1}^{t}}$	${\displaystyle A_{1}}$	${\displaystyle A_{1}^{(1)}}$	2	2	0	${\displaystyle \bullet {\stackrel {4}{\leftrightarrow }}\bullet }$	${\displaystyle 1{\stackrel {4}{\leftrightarrow }}1}$		2
${\displaystyle {\tilde {A}}_{n}}$ ${\displaystyle (n\geq 2)}$	${\displaystyle A_{n}^{u}=A_{n}^{t}}$	${\displaystyle A_{n}}$	${\displaystyle A_{n}^{(1)}}$	1	${\displaystyle n(n+1)}$	0	${\displaystyle \bullet <{\bullet -\cdots -\bullet \atop \bullet -\cdots -\bullet }>\bullet }$	${\displaystyle 1<{1-\cdots -1 \atop 1-\cdots -1}>1}$		${\displaystyle n+1}$
${\displaystyle {\tilde {B}}_{n}}$	${\displaystyle B_{n}^{u}}$	${\displaystyle B_{n}}$	${\displaystyle B_{n}^{(1)}}$	2	${\displaystyle 2n(n-1)}$	${\displaystyle 2n}$ (길이 ${\displaystyle 1}$)	${\displaystyle \bullet \Leftarrow \bullet -\cdots -\bullet <{\bullet \atop \bullet }}$	${\displaystyle 2\Leftarrow 2-\cdots -2<{1 \atop 1}}$	${\displaystyle 1\Leftarrow 2-\cdots -2<{1 \atop 1}}$	${\displaystyle 2n}$	${\displaystyle 2n-1}$
${\displaystyle {\tilde {C}}_{n}}$	${\displaystyle C_{n}^{u}}$	${\displaystyle C_{n}}$	${\displaystyle C_{n}^{(1)}}$	3	${\displaystyle 2n}$	${\displaystyle 2n(n-1)}$ (길이 1)	${\displaystyle \bullet \Rightarrow \bullet -\bullet -\cdots -\bullet -\bullet \Leftarrow \bullet }$	${\displaystyle 1\Rightarrow 2-2-\cdots -2-2\Leftarrow 1}$	${\displaystyle 1\Rightarrow 1-1-\cdots -1-1\Leftarrow 1}$	${\displaystyle 2n}$	${\displaystyle n+1}$
${\displaystyle {\tilde {D}}_{n}}$	${\displaystyle D_{n}^{u}=D_{n}^{t}}$	${\displaystyle D_{n}}$	${\displaystyle D_{n}^{(1)}}$	1	${\displaystyle 2n(n-1)}$	0	${\displaystyle {\bullet \atop \bullet }>\bullet -\bullet -\cdots -\bullet <{\bullet \atop \bullet }}$	${\displaystyle {1 \atop 1}>2-2-\cdots -2<{1 \atop 1}}$		${\displaystyle 2n-2}$
${\displaystyle {\tilde {E}}_{6}}$	${\displaystyle E_{6}^{u}=E_{6}^{t}}$	${\displaystyle E_{6}}$	${\displaystyle E_{6}^{(1)}}$	1	72	0	${\displaystyle {\bullet -\bullet \atop \bullet -\bullet }>\bullet -\bullet -\bullet }$	${\displaystyle {1-2 \atop 1-2}>3-2-1}$		12
${\displaystyle {\tilde {E}}_{7}}$	${\displaystyle E_{7}^{u}=E_{7}^{t}}$	${\displaystyle E_{7}}$	${\displaystyle E_{7}^{(1)}}$	1	126	0	${\displaystyle {\bullet -\bullet -\bullet \atop \bullet -\bullet -\bullet }>\bullet -\bullet }$	${\displaystyle {1-2-3 \atop 1-2-3}>4-2}$		18
${\displaystyle {\tilde {E}}_{8}}$	${\displaystyle E_{8}^{u}=E_{8}^{t}}$	${\displaystyle E_{8}}$	${\displaystyle E_{8}^{(1)}}$	1	240	0	${\displaystyle {\bullet \atop {}}{- \atop {}}{\bullet \atop \bullet }>\bullet -\bullet -\bullet -\bullet -\bullet -\bullet }$	${\displaystyle {2 \atop {}}{- \atop {}}{4 \atop 3}>6-5-4-3-2-1}$		30
${\displaystyle {\tilde {F}}_{4}}$	${\displaystyle F_{4}^{u}}$	${\displaystyle F_{4}}$	${\displaystyle F_{4}^{(1)}}$	2	24	24 (길이 1)	${\displaystyle \bullet -\bullet -\bullet \Rightarrow \bullet -\bullet }$	${\displaystyle 1-2-3\Rightarrow 4-2}$	${\displaystyle 1-2-3\Rightarrow 2-1}$	12	9
${\displaystyle {\tilde {G}}_{2}}$	${\displaystyle G_{2}^{u}}$	${\displaystyle G_{2}}$	${\displaystyle G_{2}^{(1)}}$	2	6	6 (길이 ${\displaystyle {\sqrt {2/3}}}$)	${\displaystyle \bullet -\bullet \Rrightarrow \bullet }$	${\displaystyle 1-2\Rrightarrow 3}$	${\displaystyle 1-2\Rrightarrow 1}$	6	4
${\displaystyle {\tilde {A}}_{2n-1}^{(2)}}$	${\displaystyle C_{n}^{t}}$	${\displaystyle B_{n}^{\vee }}$	${\displaystyle C_{n}^{(2)}}$	3	${\displaystyle 2n}$	${\displaystyle 2n(n-1)}$ (길이 1)	${\displaystyle \bullet \Rightarrow \bullet -\cdots -\bullet <{\bullet \atop \bullet }}$	${\displaystyle 1\Rightarrow 2-\cdots -2<{1 \atop 1}}$	${\displaystyle 2\Rightarrow 2-\cdots -2<{1 \atop 1}}$	${\displaystyle 2n-1}$	${\displaystyle 2n}$
${\displaystyle {\tilde {A}}_{2}^{(2)}}$	${\displaystyle BC_{1}^{m}}$	${\displaystyle BC_{1}}$	${\displaystyle {\tilde {B}}_{1}^{(2)}}$	2	${\displaystyle 2}$	${\displaystyle 2}$ (길이 ${\displaystyle 1/{\sqrt {2}}}$)	${\displaystyle \bullet {\xrightarrow {4}}\bullet }$	${\displaystyle 1{\xrightarrow {4}}2}$	${\displaystyle 2{\xrightarrow {4}}1}$	3
${\displaystyle {\tilde {A}}_{2n}^{(2)}}$ ${\displaystyle (n\geq 2)}$	${\displaystyle BC_{n}^{m}}$	${\displaystyle BC_{n}}$	${\displaystyle {\tilde {B}}_{n}^{(2)}}$	3	${\displaystyle 2n}$	${\displaystyle 2n(n-1)}$ (길이 1) ${\displaystyle 2n}$ (길이 ${\displaystyle 1/{\sqrt {2}}}$)	${\displaystyle \bullet \Rightarrow \bullet -\bullet -\cdots -\bullet -\bullet \Rightarrow \bullet }$	${\displaystyle 1\Rightarrow 2-2-\cdots -2-2\Rightarrow 2}$	${\displaystyle 2\Rightarrow 2-2-\cdots -2-2\Rightarrow 1}$	${\displaystyle 2n+1}$
${\displaystyle {\tilde {D}}_{4}^{(3)}}$	${\displaystyle G_{2}^{t}}$	${\displaystyle G_{2}^{\vee }}$	${\displaystyle G_{2}^{(3)}}$	2	6	6 (길이 ${\displaystyle {\sqrt {2/3}}}$)	${\displaystyle \bullet -\bullet \Lleftarrow \bullet }$	${\displaystyle 1-2\Lleftarrow 1}$	${\displaystyle 1-2\Lleftarrow 3}$	4	6
${\displaystyle {\tilde {D}}_{n+1}^{(2)}}$	${\displaystyle B_{n}^{t}}$	${\displaystyle C_{n}^{\vee }}$	${\displaystyle B_{n}^{(2)}}$	2	${\displaystyle 2n(n-1)}$	${\displaystyle 2n}$ (길이 1)	${\displaystyle \bullet \Leftarrow \bullet -\bullet -\cdots -\bullet -\bullet \Rightarrow \bullet }$	${\displaystyle 1\Leftarrow 1-1-\cdots -1-1\Rightarrow 1}$	${\displaystyle 1\Leftarrow 2-2-\cdots -2-2\Rightarrow 1}$	${\displaystyle n+1}$	${\displaystyle 2n}$
${\displaystyle {\tilde {E}}_{6}^{(2)}}$	${\displaystyle F_{4}^{t}}$	${\displaystyle F_{4}^{\vee }}$	${\displaystyle F_{4}^{(2)}}$	2	24	24 (길이 1)	${\displaystyle \bullet -\bullet \Rightarrow \bullet -\bullet -\bullet }$	${\displaystyle 1-2\Rightarrow 3-2-1}$	${\displaystyle 2-4\Rightarrow 3-2-1}$	9	12

아핀 리 대수의 카르탕 행렬은 딘킨 도표에서 하나의 꼭짓점을 제거하여 얻는 단순 리 대수의 카르탕 행렬 및 콕서터 라벨 · 쌍대 콕서터 라벨로 재구성할 수 있다.

Ã_n

${\displaystyle n\geq 2}$일 경우, ${\displaystyle {\tilde {A}}_{n}}$의 카르탕 행렬은 다음과 같은 ${\displaystyle (n+1)\times (n+1)}$ 대칭 정사각 행렬이다.

${\displaystyle \operatorname {Cartan} ({\tilde {A}}_{n})={\begin{pmatrix}2&-1&0&0&\cdots &0&-1\\-1&2&-1&0&\cdots &0&0\\0&-1&2&-1&\dots &0&0\\0&0&-1&2&\cdots &0&0\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&0&0&\cdots &2&-1\\-1&0&0&0&\cdots &-1&2\end{pmatrix}}}$

${\displaystyle {\tilde {A}}_{1}}$의 카르탕 행렬은 다음과 같다.

${\displaystyle \operatorname {Cartan} ({\tilde {A}}_{1})={\begin{pmatrix}2&-2\\-2&2\end{pmatrix}}}$

${\displaystyle {\tilde {A}}_{n}}$의 딘킨 도표는 ${\displaystyle n\geq 2}$일 경우 ${\displaystyle n+1}$개의 꼭짓점을 갖는 순환 그래프이다.

Ã_2n⁽²⁾

${\displaystyle n\geq 2}$일 때, ${\displaystyle {\tilde {A}}_{2n}^{(2)}}$의 카르탕 행렬은 다음과 같은 ${\displaystyle (n+1)\times (n+1)}$ 비대칭 정사각 행렬이다.

${\displaystyle \operatorname {Cartan} ({\tilde {A}}_{2n}^{(2)})={\begin{pmatrix}2&-1&0&\cdots &0&0&0\\-2&2&-1&\cdots &0&0&0\\0&-1&2&\dots &0&0&0\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots &\vdots \\0&0&0&\cdots &2&-1&0\\0&0&0&\cdots &-1&2&-1\\0&0&0&\cdots &0&-2&2\end{pmatrix}}}$

여기서 행·열 ${\displaystyle 0,1,\dots ,n}$의 순서는 다음과 같다.

${\displaystyle \alpha _{0}\Rightarrow \alpha _{1}-\cdots -\alpha _{n-1}\Rightarrow \alpha _{n}}$

${\displaystyle {\tilde {A}}_{2}^{(2)}}$의 카르탕 행렬은 다음과 같다.

${\displaystyle \operatorname {Cartan} ({\tilde {A}}_{2}^{(2)})={\begin{pmatrix}2&-1\\-4&2\end{pmatrix}}}$

여기서 행·열 0, 1의 순서는 다음과 같다.

${\displaystyle \alpha _{0}{\xrightarrow {4}}\alpha _{1}}$

G̃₂와 D̃₄⁽³⁾

${\displaystyle {\tilde {G}}_{2}}$의 근계. 여기서 ${\displaystyle \alpha =\alpha _{2}}$는 ${\displaystyle G_{2}}$의 유일한 짧은 근, ${\displaystyle \beta =\alpha _{1}}$는 ${\displaystyle G_{2}}$의 유일한 긴 근이며, ${\displaystyle \gamma =a_{1}\alpha _{1}+a_{2}\alpha _{2}=\delta }$이다. 양근은 붉은 색으로, 음은은 푸른 색으로 표시되었다. 이에 대응하는 반사 ${\displaystyle \psi _{\alpha }}$, ${\displaystyle \psi _{\beta }}$, ${\displaystyle \psi _{\gamma }}$는 ${\displaystyle {\tilde {G}}_{2}}$의 바일 군을 생성하며, 바일 군의 기본 벽감(fundamental alcove)는 직각삼각형 ${\displaystyle {\mathcal {C}}}$이다.

${\displaystyle {\tilde {G}}_{2}}$의 카르탕 행렬은 다음과 같다.

${\displaystyle \operatorname {Cartan} ({\tilde {G}}_{2})={\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-3&2\end{pmatrix}}}$

여기서 행·열 0, 1, 2의 순서는

${\displaystyle \alpha _{0}-\alpha _{1}\Rrightarrow \alpha _{2}}$

이다.

${\displaystyle {\tilde {D}}_{4}^{(3)}}$의 카르탕 행렬은 다음과 같다.

${\displaystyle \operatorname {Cartan} ({\tilde {D}}_{4}^{(3)})={\begin{pmatrix}2&-1&0\\-1&2&-3\\0&-1&2\end{pmatrix}}}$

여기서 행·열 0, 1, 2의 순서는

${\displaystyle \alpha _{0}-\alpha _{1}\Lleftarrow \alpha _{2}}$

이다.

예

${\displaystyle {\mathfrak {g}}=\mathbb {C} }$가 1차원 아벨 리 대수라고 하자. 그렇다면, 그 로랑 다항식 대수

${\displaystyle \mathbb {C} [{\mathsf {z}},{\mathsf {z}}^{-1}]}$

역시 아벨 리 대수이다. 이 경우, 중심 확대

${\displaystyle 0\to \mathbb {C} {\mathsf {k}}\to {\hat {\mathfrak {g}}}\to \mathbb {C} [{\mathsf {z}},{\mathsf {z}}^{-1}]\to 0}$

에서

${\displaystyle [{\mathsf {z}}^{m},{\mathsf {z}}^{n}]=\delta _{m+n,0}m{\mathsf {k}}}$

${\displaystyle [{\mathsf {k}},{\mathsf {z}}^{m}]=0}$

이 된다. 이 경우,

${\displaystyle {\mathsf {z}}^{-n}={\sqrt {n}}{\mathsf {p}}_{n}\qquad (n>0)}$

${\displaystyle {\mathsf {z}}^{n}={\sqrt {n}}{\mathsf {q}}_{n}\qquad (n>0)}$

${\displaystyle {\mathsf {k}}=\hbar }$

로 놓으면,

${\displaystyle [{\mathsf {q}}_{m},{\mathsf {p}}_{n}]=\delta _{m,n}\hbar }$

가 되어, 이는 무한 차원 하이젠베르크 리 대수와 (${\displaystyle {\mathsf {z}}^{0}}$으로 생성되는) 1차원 아벨 리 대수의 직합이 된다.^[7]:§2.4 특히, 이는 무한 차원 보손 포크 공간 ${\displaystyle \mathbb {C} [{\mathsf {x}}_{1},{\mathsf {x}}_{2},\dotsb ]}$ 위에 표준적으로 작용한다.^[7]:(2.19)

이 경우, 스가와라 구성은 다음과 같다.^[7]:(2.23)

${\displaystyle {\mathsf {L}}_{n}=-{\frac {1}{2}}\sum _{m\in \mathbb {Z} }{\mathsf {z}}^{\min\{m,n-m\}}{\mathsf {z}}^{\max\{m,n-m\}}}$

${\displaystyle {\mathsf {c}}=1}$

물리학적으로, 이는 자유 보손에 대한 2차원 등각 장론에 해당한다.

역사

아핀 리 대수는 (다른 카츠-무디 대수와 함께) 빅토르 카츠와 로버트 무디(영어: Robert Moody)가 발견하였다. ‘아핀’이라는 이름은 그 바일 군이 근계에 아핀 변환으로 작용하기 때문이다.

스가와라 구성은 스가와라 히로타카(일본어: 菅原 寛孝 (すがわら ひろたか))가 1968년에 발견하였다.^[12] 공액 구성은 피터 고더드(영어: Peter Goddard, 1945〜) · 에이드리언 켄트(영어: Adrian Kent) · 데이비드 올리브(영어: David Olive, 1937〜2012)가 1985년에 발견하였다.^{[13] [9]}