Непрекинатост на функција

Нeпрекината функција — функција кај која мала промена на аргументот предизвикува мала промена на вредноста на функцијата. Ова значи дека нема нагли промени во вредноста, познати како прекини (дисконтинуитети) или скокови. Попрецизно, една функција е непрекината ако може да се добијат произволно мали промени во нејзината вредност преку ограничување на промените на нејзиниот аргумент. Дисконтинуирана функција или функција со прекин е функција која не е непрекината. До XIX век, математичарите во голема мера се потпирале на интуитивните поими за непрекинатост и разгледувале само непрекинати функции. Епсилон-делта дефиницијата на гранична вредност била воведена за да се формализира дефиницијата за непрекинатост.

Статии поврзани со математичката анализа

Основна теорема на анализата Лимес на функција Непрекинатост Векторска анализа Теорија на редови Теорија на низи Тензорско сметање

Диференцијално сметање

Извод од производ Извод од количник Извод на сложена функција Извод на имплицитна функција Формула на Тејлор Теореми за средна вредност

Интегрално сметање

Таблица на основни интеграли Несвојствен интеграл

Методи на интегрирање

Интегрирање по делови Интегрирање со смена Ојлерови смени Тригонометриски смени Портал: Математика

Непрекинатоста е еден од основните поими во калкулусот и на математичката анализа, каде што аргументите и вредностите на функциите се реални и комплексни броеви. Концептот се генерализира кај функции помеѓу метрички простори и кај функции помеѓу тополошки простори. Последните се најопштите непрекинати функции, а нивната дефиниција е основа за топологијата .

Посилна форма на непрекинатост е рамномерната непрекинатост. Во теоријата за подредување, особено во теоријата на домен, концепт кој е поврзан со непрекинатоста е непрекинатоста на Скот .

Како пример, функцијата ${\displaystyle H(t)}$ што ја означува висината на растечкиот цвет во временскиот момент ${\displaystyle t}$ би се сметала за непрекината. Спротивно на тоа, функцијата ${\displaystyle M(t)}$ што го означува износот на пари на банкарска сметка во временскиот момент ${\displaystyle t}$ не е непрекината бидејќи таа „скока“ во секој момент од времето кога парите се депонираат или се повлекуваат.

Историја

Еден облик на епсилон-делта дефиницијата за непрекинатост првпат била дадена од Бернард Болцано во 1817 година. Огистен-Луј Коши ја дефинирал непрекинатоста на ${\displaystyle y=f(x)}$ на следниов начин: при бескрајно малa прoмена ${\displaystyle \alpha }$ на независната променлива ${\displaystyle x}$ секогаш се добива бесконечно мала промена ${\displaystyle f(x+\alpha )-f(x)}$ на зависната променлива ${\displaystyle y}$ (види на пр. Cours d'Analyse, стр.34). Коши дефинирал бесконечно мали величини во однос на променливите величини, а неговата дефиниција за непрекинатост е тесно поврзана со дефиницијата на бесконечно мала величина која се користи и денес (види микронепрекинатост). Формалната дефиниција и разликата помеѓу непрекинатост во точка и рамномерна непрекинатост првпат ја дал Болцано во 1830-те, но делото не било објавено дури до 1930-те. Како и Болцано,^[1] Карл Вајерштрас^[2] не прифаќал непрекинатост на функција во точка ${\displaystyle c}$ освен ако таа не е дефинирана и од двете страни на ${\displaystyle c}$, но Едуард Гурсат^[3] дозволил непрекинатоста на функција да може да се дефинира само во точка или само на едната страна од точка ${\displaystyle c}$, додека Камил Жордан^[4] дал дефиниција според која функција може да биде дефинирана само во точката ${\displaystyle c}$. Сите овие три нееквивалентни дефиниции за непрекинатост во точка сè уште се во употреба.^[5] Едуард Хајне е првиот кој ја публикувал дефиницијата за рамномерна непрекинатост во 1872 година, но овие идеи ги засновал на предавањата што ги одржал Петер Густав Лежен Дирихле во 1854 година.^[6]

Реални функции

Дефиниција

Функцијата ${\displaystyle f(x)={\tfrac {1}{x}}}$ е непрекината на својот домен${\displaystyle D_{f}=\mathbb {R} \setminus \{0\}}$, но има прекин точката во ${\displaystyle x=0,}$ па затоа таа се смета како по делови непрекината функција. ^[7]

Реална функција, т.е. функција од множеството на реални броеви во множеството на реални броеви може да се претстави со график во Декартовата рамнина; таквата функција е непрекината ако, грубо кажано, графикот е единствена непрекината крива чиј домен е целата реална права. Подолу е дадена математички поригорозна дефиниција. ^[8]

Непрекинатоста на реалните функции обично се дефинира преку гранични вредности (лимеси). Функција ${\displaystyle f}$ од променлива ${\displaystyle x}$ е непрекината во реалниот број ${\displaystyle c\,,}$ ако лимесот на ${\displaystyle f(x)}$ кога ${\displaystyle x}$ се стреми кон ${\displaystyle c\,,}$ е еднаков на ${\displaystyle f(c).}$

Постојат неколку различни дефиниции за (глобална) непрекинатост на функција, кои зависат од природата на нејзиниот домен.

Функцијата е непрекината на отворен интервал ако интервалот е содржан во доменот на функцијата и функцијата е непрекината во секоја негова точка. Функција која е непрекината на интервалот ${\displaystyle (-\infty ,+\infty )}$ (целата реална права) многу често едноставно се нарекува непрекината функција; исто така, се вели дека таквата функција е насекаде непрекината. На пример, сите полиномни функции се насекаде непрекинати.

Функцијата е непрекината на полуотворен или затворен интервал ако интервалот е содржан во доменот на функцијата, функцијата е непрекината во секоја внатрешна точка на интервалот, а вредноста на функцијата во секоја крајна точка што припаѓа на интервалот е лимес на вредностите на функцијата кога променливата се стреми кон крајната точка од внатрешноста на интервалот. На пример, функцијата ${\displaystyle f(x)={\sqrt {x}}}$ е непрекината на целиот нејзин домен, т.е. на затворениот интервал ${\displaystyle [0,+\infty ).}$

Многу често се среќаваат функции дефинирани по делови. Тоа се функции кои се дефинирани на множество добиено така што од целото ${\textstyle \mathbb {R} }$ се исфрлени некои изолирани точки. Примери за вакви функции се реципрочната функција ${\textstyle x\mapsto {\frac {1}{x}}}$ и функцијата тангенс ${\displaystyle x\mapsto {\text{tg}}x.}$ Кога функција е непрекината на целиот нејзин домен, во некои контексти се вели дека таа функција е непрекината, иако, во суштина таа не е непрекината во реалните броеви во кои не е дефинирана. Во други контексти, главно кога некој е заинтересиран за однесувањето на некоја ваква функција во близина на нејзините исклучителни точки, се вели дека таа има прекин, т.е. дека е дисконтинуирана.

Функција дефинирана по делови е дисконтинуирана или има прекин во точка ако таа точка му припаѓа на тополошкиот затворач на нејзиниот домен и, или точката не му припаѓа на доменот на функцијата или функцијата не е непрекината во таа точка. На пример, функциите ${\textstyle x\mapsto {\frac {1}{x}}}$ и ${\textstyle x\mapsto \sin({\frac {1}{x}})}$ не се непрекинати во 0 и без разлика на тоа која вредност ќе се избере за нивно дефинирање во 0, тие остануваат дисконтинуирани во 0. Точката во која функцијата е дисконтинуирана се нарекува точка на прекин.

Постојат неколку начина за дефинирање на непрекината функција во смисла на начините споменати погоре, со користење на математичка нотација.

Нека $${\displaystyle f:D\to \mathbb {R} }$$е функција дефинирана на ${\displaystyle D}$-подмножество на множеството од реални броеви.

Множеството ${\displaystyle D}$ е доменот на ${\displaystyle f\,.}$ Најчесто среќавани случаи се следниве:

• ${\displaystyle D=\mathbb {R} \,,}$ т.е. ${\displaystyle D}$ е целото множество од реални броеви.
• За реални броеви ${\displaystyle a}$ и ${\displaystyle b\,,}$
  • ${\displaystyle D=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}\,;}$ ${\displaystyle D}$ е затворен интервал или
  • ${\displaystyle D=(a,b)=\{x\in \mathbb {R} \mid a<x<b\}\,;}$ ${\displaystyle D}$ е отворен интервал .

Во случајот кога доменот ${\displaystyle D}$ е отворен интервал, ${\displaystyle a}$ и ${\displaystyle b}$ не му припаѓаат на ${\displaystyle D\,,}$ a вредностите ${\displaystyle f(a)}$ и ${\displaystyle f(b)}$ не се важни за непрекинатоста на ${\displaystyle f}$ над ${\displaystyle D\,.}$

Дефиниција преку лимес на функција

Функцијата ${\displaystyle f,}$ е непрекината во некоја точка ${\displaystyle c}$ од нејзиниот домен ако лимесот на ${\displaystyle f(x),}$ кога ${\displaystyle x}$ се приближува кон ${\displaystyle c}$ во доменот на ${\displaystyle f,}$ постои и е еднаков на ${\displaystyle f(c).}$ ^[9] Во математичка нотација, ова се пишува како $${\displaystyle \lim _{x\to c}{f(x)}=f(c).}$$Ова подетално значи дека мора да се исполнети три услова: прво, ${\displaystyle f,}$ треба да е дефинирана во ${\displaystyle c}$ (гарантирано со барањето ${\displaystyle c}$ да е во доменот на ${\displaystyle f}$); второ, лимесот на левата страна од равенката мора да постои; трето, вредноста на оваа граница мора да биде еднаква на ${\displaystyle f(c).}$

(Овде, претпоставивме дека доменот на ${\displaystyle f}$ нема изолирани точки.)

Дефиниција преку околини

Околина нa точка ${\displaystyle c}$ е множество кое ги содржи сите точки кои се на растојание од точката ${\displaystyle c}$ помало од некој фиксен број. Интуитивно, функција е непрекината во точката ${\displaystyle c}$ ако досегот на ${\displaystyle f}$ над околина на ${\displaystyle c}$ се стреми кон еднолементното множество ${\displaystyle \{f(c)\}}$ кога ширината на околината околу ${\displaystyle c}$ се стреми кон нула. Попрецизно, функција ${\displaystyle f}$ е непрекината во точката ${\displaystyle c}$ oд нејзиниот домен ако за секоја околина ${\displaystyle N_{1}(f(c))}$ постои околина ${\displaystyle N_{2}(c)}$ во нејзиниот домен таква што ${\displaystyle f(x)\in N_{1}(f(c))}$ за секој ${\displaystyle x\in N_{2}(c)}$ или поинаку запишано ${\displaystyle f(N_{2}(c))\subseteq N_{1}(f(c))\,.}$

Бидејќи околини се дефинираат во секој тополошки простор, оваа дефиниција за непрекината функција се применува не само за реални функции, туку и кога доменот и кодоменот се тополошки простори и затоа таа е најопштата дефиниција за непрекинатост. Од неа, следува дека функцијата автоматски е непрекината во секоја изолирана точка од нејзиниот домен. На пример, секоја реална функција со домен на целите броеви е непрекината.

Дефиниција преку гранични вредности (лимеси) на низи

Низата exp(1/n) конвергира кон exp(0) = 1

Функцијата ${\displaystyle f}$ е непрекината во точката ${\displaystyle c}$ ако за која било низа ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ од точки во доменот која конвергира кон ${\displaystyle c\,,}$ соодветната низа ${\displaystyle \left(f(x_{n})\right)_{n\in \mathbb {N} }}$ конвергира кон ${\displaystyle f(c).}$ Во математичка нотација, $${\displaystyle \forall (x_{n})_{n\in \mathbb {N} }\subset D:\lim _{n\to \infty }x_{n}=c\Rightarrow \lim _{n\to \infty }f(x_{n})=f(c)\,.}$$

Дефиниции на Вајерштрас и Џордан (епсилон-делта) за непрекинати функции

Илустрација на ${\displaystyle \varepsilon -\delta }$- дефиницијата за непрекинатост: кога ${\displaystyle x=2}$, секоја вредност ${\displaystyle \delta \leqslant 1/2}$ го задоволува условот од дефиницијата за ${\displaystyle \varepsilon =1/2\,.}$

Ако експлицитно ја вклучиме дефиницијата за лимес на функција, добиваме нова дефиниција. За дадена функција ${\displaystyle f:D\to \mathbb {R} }$ и елемент ${\displaystyle x_{0}}$ од доменот ${\displaystyle D}$, се вели дека ${\displaystyle f}$ е непрекинатa во точката ${\displaystyle x_{0}}$ ако важи следново: за кој било позитивен реален број ${\displaystyle \varepsilon >0,}$ колку и да е мал, постои позитивен реален број ${\displaystyle \delta >0}$ таков што за секој ${\displaystyle x}$ од доменот на ${\displaystyle f}$ за кој ${\displaystyle x_{0}-\delta <x<x_{0}+\delta ,}$ вредноста на ${\displaystyle f(x)}$ ги задоволува $${\displaystyle f\left(x_{0}\right)-\varepsilon <f(x)<f(x_{0})+\varepsilon .}$$

Поинаку запишано, непрекинатоста на ${\displaystyle f:D\to \mathbb {R} }$ во ${\displaystyle x_{0}\in D}$ значи дека за секој ${\displaystyle \varepsilon >0,}$ постои ${\displaystyle \delta >0}$ така што за сите ${\displaystyle x\in D}$ : $${\displaystyle \left|x-x_{0}\right|<\delta \Rightarrow |f(x)-f(x_{0})|<\varepsilon .}$$

Поинтуитивно, можеме да кажеме дека ако сакаме сите вредности ${\displaystyle f(x)}$ да останат во некоja малa околина на ${\displaystyle f\left(x_{0}\right),}$ треба да избереме доволно мала околина вредности на ${\displaystyle x}$ околу ${\displaystyle x_{0}.}$ Ако можеме да го направиме тоа без разлика колку е мала околината на ${\displaystyle f(x_{0})\,,}$, тогаш ${\displaystyle f}$ е непрекината во ${\displaystyle x_{0}.}$

Во современи термини, ова се генерализира со дефиницијата за непрекинатост на функција во однос на базата за топологијата, која овде е метричката топологија.

Вајерштрас барал интервалот ${\displaystyle x_{0}-\delta <x<x_{0}+\delta }$ да биде целосно во доменот ${\displaystyle D}$, но Жордан го отстранил тоа ограничување.

Дефиниција преку контрола на остатокот

Во доказите и нумеричката анализа, честопати треба да знаеме колку брзо конвергираат лимесите, или со други зборови, да го контролираме остатокот. Ова може да се формализира со дефиницијата за непрекинатост. Функција ${\displaystyle C:[0,\infty )\to [0,\infty ]}$ се нарекува контролна функција ако

• ${\displaystyle C}$ е неопаѓачка
• ${\displaystyle \inf _{\delta >0}C(\delta )=0}$

Функција ${\displaystyle f:D\to R}$ е ${\displaystyle C-}$непрекината во ${\displaystyle x_{0}}$ ако постои околина ${\textstyle N(x_{0})}$ на која$${\displaystyle |f(x)-f(x_{0})|\leq C\left(\left|x-x_{0}\right|\right){\text{ за секој }}x\in D\cap N(x_{0})\,.}$$

Една функција е непрекината во ${\displaystyle x_{0}}$ ако е ${\displaystyle C-}$непрекината за некоја контролна функција ${\displaystyle C\,.}$

Овој пристап природно води кон усовршување на поимот за непрекинатост со ограничување на множеството од дозволени контролни функции. За дадено множество ${\displaystyle {\mathcal {C}}}$ од контролни функции, велиме дека функција е ${\displaystyle {\mathcal {C}}}$-непрекината ако е ${\displaystyle C-}$непрекината за некоја контролна функција ${\displaystyle C\in {\mathcal {C}}.}$ На пример, непрекинатите функции според Липшиц и непрекинатите функции од експонент ${\displaystyle \alpha }$ според Холдер редоследно се дефинирани преку множеството од контролни функции $${\displaystyle {\mathcal {C}}_{\mathrm {Lipschitz} }=\{C:C(\delta )=K|\delta |,\ K>0\}}$$и$${\displaystyle {\mathcal {C}}_{{\text{Hölder}}-\alpha }=\{C:C(\delta )=K|\delta |^{\alpha },\ K>0\}.}$$

Дефиниција со помош на осцилација

Прекинот на функција во точка се квантифицира (се мери) преку нејзината осцилација.

Непрекинатоста може да се дефинира и преку поимот за осцилација: функцијата ${\displaystyle f}$ е непрекината во точка ${\displaystyle x_{0}}$ ако и само ако неjзината осцилација во таа точка е нула; ^[10] симболично запишано, ${\displaystyle \omega _{f}(x_{0})=0\,.}$ Придобивка од оваа дефиниција е тоа што се квантификува степенот на прекинатост: осцилацијата дава мера за тоа колкав е прекинот на функцијата во една точка.

Оваа дефиниција е корисна во описната теорија на множества за проучување на множествата од точки на прекин и на непрекинатите точки. Имено, непрекинати точки се точките кои му припаѓаат на пресекот на множествата во кои осцилацијата е помала од ${\displaystyle \varepsilon }$ (според тоа е <span about="#mwt346" class="mwe-math-element" data-mw="{&quot;name&quot;:&quot;math&quot;,&quot;attrs&quot;:{},&quot;body&quot;:{&quot;extsrc&quot;:&quot;G_{\\delta}&quot;}}" id="7" typeof="mw:Extension/math"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math xmlns="http://www.w3.org/1998/Math/MathML"> <semantics> <mrow class="MJX-TeXAtom-ORD"> <mstyle scriptlevel="0" displaystyle="true"> <msub> <mi>G</mi> <mrow class="MJX-TeXAtom-ORD"> <mi>δ</mi> </mrow> </msub> </mstyle> </mrow> <annotation encoding="application/x-tex">{\displaystyle G_{\delta }}</annotation> </semantics> </math></span><img alt="{\displaystyle G_{\delta }}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" data-cx="{&quot;adapted&quot;:false}" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7b42b79015590af928aa28bda9514373aeac0e1e" style="vertical-align: -0.671ex; width:2.8ex; height:2.509ex;"></span> множество). Преку нив се добива брз доказ за едната насока на условот за интеграбилност на Лебег (Lebesgue).^[11]

Дефиницијата на непрекинатост преку осцилација е еквивалентна на ${\displaystyle \varepsilon -\delta }$ дефиницијата со едноставно преуредување и со користење на лимеси (lim sup, lim inf) за дефинирање на осцилацијата: ако (во дадена точка) за дадено ${\displaystyle \varepsilon _{0}}$ нема ${\displaystyle \delta }$ кое ги задоволува условите на ${\displaystyle \varepsilon -\delta }$ дефиницијата, тогаш осцилацијата е барем ${\displaystyle \varepsilon _{0},}$ и обратно ако за секој ${\displaystyle \varepsilon }$ постои такво ${\displaystyle \delta ,}$ осцилацијата е 0. Дефиницијата на осцилацијата на функција може природно да се прошири (генерализира) на пресликувања од тополошки простор во метрички простор .

Дефиниција преку хиперреали

Коши ја дефинирал непрекинатоста на функцијата преку следниве интуитивни термини: бесконечно мала промена на независната променлива одговара на бесконечно мала промена на зависната променлива (види Cours d'analyse, страница 34). Нестандардната анализа е начин ова да се направи математички ригорозно. Реалната права се проширува со додавање на бесконечности (бесконечно големи) и на инфинитезимални (бесконечно мали) величини при што се формира множеството од хиперреалните броеви. Во нестандардната анализа, непрекинатоста може да се дефинира на следниов начин.

 

Реална функција ${\displaystyle f}$ е непрекината по ${\displaystyle x}$ ако нејзината природна екстензија на хиперреалите има својство дека за секоја инфинитезимала ${\displaystyle dx,}$ величината ${\displaystyle f(x+dx)-f(x)}$ е инфинитезимала^[12].

(видете и микронепрекинатост). Со други зборови, бесконечно мало зголемување на независната променлива секогаш предизвикува бесконечно мала промена на зависната променлива, давајќи модерен израз на дефиницијата за непрекинатост на Огистен-Луј Коши (Augustin-Louis Cauchy) .

Конструкција на непрекинати функции

Графикот на кубната функција нема скокови или дупки. Функцијата е непрекината.

Проверката на непрекинатоста на дадена функција може да се поедностави со проверка на некое од горенаведените дефинирачки својства за составните блокови на таа функција. Едноставно е да се докаже дека збирот на две функции кои се непрекинати на некој домен е исто така непрекината функција на тој домен. Збирот на непрекинатите функции$${\displaystyle f,g\colon D\to \mathbb {R} ,}$$т.е. функцијата $${\displaystyle s=f+g}$$ дефинирана со ${\displaystyle s(x)=f(x)+g(x)}$ за секој ${\displaystyle x\in D\,,}$ е непрекинатa на ${\displaystyle D.}$

Истото важи и за производот на две непрекинати функции, $${\displaystyle p=f\cdot g}$$ (дефиниран со ${\displaystyle p(x)=f(x)\cdot g(x)}$ за сите ${\displaystyle x\in D}$). Tој е непрекинатa функција на ${\displaystyle D.}$

Со комбинирање на горенаведените запазувања на непрекинатоста и од непрекинатоста на константните функции и на функцијата идентитет ${\displaystyle I(x)=x}$ на ${\displaystyle \mathbb {R} }$, се доаѓа до непрекинатоста на секоја полиномна функција на ${\displaystyle \mathbb {R} ,}$ како на пример$${\displaystyle f(x)=x^{3}+x^{2}-5x+3}$$ (прикажана на цртежот на десната страна).

Графикот на непрекината рационална функција. Функцијата не е дефинирана во ${\displaystyle x=-2.}$ Вертикалната и хоризонталната права се асимптоти на функцијата.

Слично може да се докаже дека и реципрочната функција на непрекината функција $${\displaystyle r=1/f}$$(дефинирана со ${\displaystyle r(x)=1/f(x)}$ за сите ${\displaystyle x\in D}$ за кои ${\displaystyle f(x)\neq 0}$) е непрекината на множеството ${\displaystyle D\setminus \{x:f(x)=0\}.}$

Од ова следува дека функцијата количник на непрекинати функции$${\displaystyle q=f/g}$$(дефинирана со ${\displaystyle q(x)=f(x)/g(x)}$ за сите ${\displaystyle x\in D}$, за кои ${\displaystyle g(x)\neq 0}$) е непрекината функција на ${\displaystyle D\setminus \{x:g(x)=0\}\,.}$

На пример, функцијата (прикажана на цртежот) $${\displaystyle y(x)={\frac {2x-1}{x+2}}}$$е дефинирана за секoj реален број ${\displaystyle x\neq -2}$ и е непрекината во секоја таква точка. Според тоа, таа е непрекината функција. Прашањето за непрекинатост во ${\displaystyle x=-2}$ не е релевантно бидејќи ${\displaystyle x=-2}$ не е во доменот на ${\displaystyle y.}$ Не постои непрекината функција ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$ која се совпаѓа со ${\displaystyle y(x)}$ за сите ${\displaystyle x\neq -2.}$

Графици на функциите sinc и на cos.

Бидејќи функцијата синус е непрекината на целото множество од реални броеви, функцијата sinc дефинирана со ${\displaystyle G(x)=\sin(x)/x,}$ е дефинирана и непрекината за секој реален ${\displaystyle x\neq 0.}$ Меѓутоа, за разлика од претходниот пример, ${\displaystyle G}$ може да се продолжи до непрекината функција на целото ${\displaystyle \mathbb {R} }$, преку (до)дефинирање на вредноста ${\displaystyle G(0)=1}$ што е еднакво на лимесот на ${\displaystyle G(x),}$ кога ${\displaystyle x}$ се стреми кон 0, т.е. $${\displaystyle G(0)=\lim _{x\to 0}{\frac {\sin x}{x}}=1.}$$

Така, екстензијата на

${\displaystyle G(x)={\begin{cases}{\frac {\sin(x)}{x}}&{\text{ ако }}x\neq 0\\1&{\text{ ако }}x=0,\end{cases}}}$

функцијата sinc e непрекината на целотo ${\displaystyle \mathbb {R} \,.}$ Терминот отстранлив сингуларитет се користи во вакви случаи, т.е. кога (до)дефинирањето на вредностите на функцијата за да се совпаѓаат со соодветните лимеси ја прави функцијата непрекината во одредени проблематични точки во кои оригиналната функција на е дефинирана.

Малку посложена е конструкцијата на непрекинати функции преку композиција (состав) на функции. Ако се дадени непрекинатите функции $${\displaystyle g:D_{g}\subseteq \mathbb {R} \to R_{g}\subseteq \mathbb {R} \quad {\text{ и }}\quad f:D_{f}\subseteq \mathbb {R} \to R_{f}\subseteq D_{g},}$$тогаш нивната композиција (состав), означена со ${\displaystyle c=g\circ f:D_{f}\to \mathbb {R} ,}$ и дефинирана со ${\displaystyle c(x)=g(f(x)),}$ е непрекината.

Оваа конструкција овозможува да се заклучи дека, на пример функцијата$${\displaystyle e^{\sin(\ln x)}}$$е прекината за секој ${\displaystyle x>0.}$

Примери на функции кои не се непрекинати

График на функцијата signum. Гледаме дека ${\displaystyle \lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)}$. Затоа функцијата signum има прекин во 0.

Пример за функција со прекин е функцијата-чекор на Хевисајд (Heaviside) ${\displaystyle H}$, дефинирана со $${\displaystyle H(x)={\begin{cases}1&{\text{ ако }}x\geq 0\\0&{\text{ ако }}x<0\end{cases}}}$$

Нека, на пример, ${\displaystyle \varepsilon =1/2.}$ Тогаш не постои ${\displaystyle \delta }$-околина на ${\displaystyle x=0,}$ односно нема отворен интервал ${\displaystyle (-\delta ,\;\delta )}$ со ${\displaystyle \delta >0,}$ за кој сите вредности на ${\displaystyle H(x)}$ ќе бидат во рамките на ${\displaystyle \varepsilon }$-околината на ${\displaystyle H(0),}$ односно во рамките на ${\displaystyle (1/2,\;3/2)}$ . Интуитивно, можеме да го замислиме овој тип на прекин како ненадеен скок во вредностите на функцијата.

Слично на тоа, функцијата signum (или знак) $${\displaystyle \operatorname {sgn}(x)={\begin{cases}\;\;\ 1&{\text{ ако }}x>0\\\;\;\ 0&{\text{ ако }}x=0\\-1&{\text{ ако }}x<0\end{cases}}}$$има прекин во ${\displaystyle x=0}$, но е непрекината во секоја друга точка. Друг пример е функцијата $${\displaystyle f(x)={\begin{cases}\sin \left(x^{-2}\right)&{\text{ if }}x\neq 0\\0&{\text{ if }}x=0\end{cases}}}$$која е непрекината секаде освен во ${\displaystyle x=0.}$

График на функцијата на Тома на интервалот (0,1). За најгорната точка во средината важи f(1/2) = 1/2.

Покрај претходно спомнатите точки на непрекинатост и прекините, постојат и функции чие однесување, често се нарекува патолошко. На пример, функцијата на Тома, $${\displaystyle f(x)={\begin{cases}1&{\text{ ако }}x=0\\{\frac {1}{q}}&{\text{ ако }}x={\frac {p}{q}}{\text{ e рационален број при што НЗД(p,q)=1}}\\0&{\text{ ако }}x{\text{ е ирационален}}.\end{cases}}}$$е непрекината во секој ирационален број и има прекин во секој рационален број. Слично, функцијата на Дирихле, или функцијата индикатор за множеството од рационални броеви, $${\displaystyle D(x)={\begin{cases}0&{\text{ ако }}x\in \mathbb {R} \setminus \mathbb {Q} \\1&{\text{ ако }}x\in \mathbb {Q} \end{cases}}}$$ никаде не е непрекината, т.е. има прекин во секој реален број.

Својства

Корисна лема

Нека ${\displaystyle f(x)}$ е функција која е непрекината во точката ${\displaystyle x_{0}}$ и ${\displaystyle f(x_{0})\neq y_{0}\,.}$ Тогаш, постои некоја околина ${\displaystyle N(x_{0})}$ на ${\displaystyle x_{0}}$, т.ш. ${\displaystyle f(x)\neq y_{0}}$ за секој ${\displaystyle x\in N(x_{0}).}$^[13]

Доказ: Според дефиницијата за непрекинатoст, за ${\displaystyle \varepsilon ={\frac {|y_{0}-f(x_{0})|}{2}}>0}$, постои ${\displaystyle \delta >0}$ за кое $${\displaystyle \left|f(x)-f(x_{0})\right|<{\frac {\left|y_{0}-f(x_{0})\right|}{2}}\quad {\text{ кога }}\quad |x-x_{0}|<\delta }$$Ако претпоставиме дека има точка во околината ${\displaystyle |x-x_{0}|<\delta }$ за која ${\displaystyle f(x)=y_{0},}$ тогаш се добива противречноста $${\displaystyle \left|f(x_{0})-y_{0}\right|<{\frac {\left|f(x_{0})-y_{0}\right|}{2}}.}$$

Теорема за средна вредност

Теоремата за средна вредност е теорема за постоење (егзистенцијална теорема), заснована на својството за комплетност на множеството од реалните броеви. Таа гласи:

Ако реалната функција f е непрекината на затворениот интервал ${\displaystyle [a,b],}$ а k е некој број помеѓу ${\displaystyle f(a)}$ и ${\displaystyle f(b),}$ тогаш постои некој број ${\displaystyle c\in [a,b],}$ таков што ${\displaystyle f(c)=k.}$

На пример, ако детето порасне од 1m до 1,5m во периодот кога неговата возраст е помеѓу две и шест години, тогаш во одреден момент од тој временски период, висината на детето мора да била 1,25m.

Како последица, ако ${\displaystyle f}$ е непрекинатa на ${\displaystyle [a,b]}$ и ${\displaystyle f(a)}$ и ${\displaystyle f(b)}$ се разликуваат според нивниот (пред)знак, т.е. ако ${\displaystyle f(a)\cdot f(b)<0}$, тогаш постои некоја точка ${\displaystyle c\in [a,b]}$ во која ${\displaystyle f(c)=0.}$

Теорема за екстремни вредности

Теоремата за екстремна вредност гласи: ако функцијата ${\displaystyle f}$ е дефинирана на затворен интервал ${\displaystyle [a,b]}$ (или на некое затворено и ограничено множество) и таму е непрекината, тогаш функцијата го достигнува својот максимум на ${\displaystyle [a,b],}$ т.е. постои ${\displaystyle c\in [a,b]}$ за кое ${\displaystyle f(c)\geq f(x)}$ за сите ${\displaystyle x\in [a,b].}$ Истото важи и за минимумот на функцијата ${\displaystyle f}$. Овие искази, генерално, не се вистинити ако функцијата е дефинирана на отворен интервал ${\displaystyle (a,b)}$ (или на кое било множество што не е затворено или ограничено). На пример, непрекинатата функција ${\displaystyle f(x)={\frac {1}{x}},}$ дефинирана на отворениот интервал ${\displaystyle (0,1),}$ не го достигнува својот максимум, бидејќи на него таа не е ограничена одгоре.

Поврзаност со диференцијабилноста и интеграбилноста

Секоја диференцијабилна функција $${\displaystyle f:(a,b)\to \mathbb {R} }$$е непрекината, што може лесно да се докаже. Обратното не важи: на пример, функцијата апсолутна вредност

${\displaystyle f(x)=|x|={\begin{cases}\;\;\ x&{\text{ ако }}x\geq 0\\-x&{\text{ ако }}x<0\end{cases}}}$

е насекаде непрекината. Сепак, таа не е диференцијабилна во ${\displaystyle x=0}$ (иако е диференцијабилна во секоја друга точка). Исто така, функцијата на Вајерштрас е насекаде непрекината, но не е диференцијабилна во ниту една точка.

Изводот ${\displaystyle f'(x)}$ на диференцијабилна функција ${\displaystyle f(x)}$ не мора да биде непрекината функција. Ако ${\displaystyle f'(x)}$ е непрекинат, за ${\displaystyle f(x)}$ се вели дека е непрекинатoдиференцијабилнa. Mножеството од непрекинатoдиференцијабилни функции на множество ${\displaystyle \Omega }$ се означува со ${\displaystyle C^{1}(\Omega ).}$ Поопшто, множеството од функции $${\displaystyle f:\Omega \to \mathbb {R} }$$(од отворен интервал или отворено подмножество ${\displaystyle \Omega \subseteq \mathbb {R} }$) такви што секоја од нив е ${\displaystyle n}$-пати диференцијабилна и такви што секој ${\displaystyle n}$ -ти извод $${\displaystyle f^{(n)}}$$е непрекинат, се означува ${\displaystyle C^{\,n}(\Omega )}$ (видете го написот класа на диференцијабилност). Во областа компјутерска графика, својствата поврзани (но не и идентични) со ${\displaystyle C^{0},C^{1},C^{2}}$ понекогаш се нарекуваат ${\displaystyle G^{0}}$ (непрекинатост на позиција), ${\displaystyle G^{1}}$ (непрекинатост на тангенција), и ${\displaystyle G^{2}}$ (непрекинатост (континуитет) на искривување); погледнете го делот глаткост (мазност) на криви и површини.

Секоја непрекината функција $${\displaystyle f:[a,b]\to \mathbb {R} }$$е интеграбилна (на пример, во смисла на Риманов интеграл). Обратното не важи; на пример, функцијата знак е интеграбилна, но не е непрекината).

Конвергенција по точки и рамномерна (униформна) конвергенција

Низа од непрекинати функции ${\displaystyle f_{n}(x)}$ чија гранична вредност по точки ${\displaystyle f(x)}$ не е непрекината функција. Низата не конвергира рамномерно.

Нека е дадена низа од функции $${\displaystyle f_{1},f_{2},\dotsc :I\to \mathbb {R} }$$такви што лимесот$${\displaystyle f(x):=\lim _{n\to \infty }f_{n}(x)}$$постои за секое ${\displaystyle x\in D.}$ Добиената функција ${\displaystyle f(x)}$ се нарекува лимес по точки на низата функции ${\displaystyle \left(f_{n}\right)_{n\in \mathbb {N} }.}$ Лимесот по точки не мора да биде непрекината функција, дури и ако сите функции ${\displaystyle f_{n}}$ се непрекинати, како што е покажано со анимацијата десно. Меѓутоа, ${\displaystyle f}$ е непрекината ако сите функции ${\displaystyle f_{n}}$ се непрекинати и низата ${\displaystyle \left(f_{n}\right)_{n\in \mathbb {N} }}$ конвергира рамномерно, што е резултат познат како теорема за рамномерна (униформа) конвергенција. Оваа теорема може да се користи за да се покаже дека експоненцијалните функции, логаритамските функции, функцијата квадратен корен и тригонометриските функции се непрекинати.

Непрекинатост по насока и полунепрекинатост

• 
  Oддеснонепрекината функција
• 
  Одлевонепрекината функција

Непрекинатите функции може да бидат непрекинати во поограничена смисла, што нé доведува до концептите за непрекинатост по насока (или непрекинатост оддесно или одлево) и за полунепрекинатост. Грубо кажано, функција е оддеснонепрекината (непрекината оддесно) ако не постои скок кога кон граничната точка се приближуваме оддесно. Формално, се вели дека ${\displaystyle f}$ е оддеснонепрекината во точката ${\displaystyle c}$ ако важи следново: за кој било број ${\displaystyle \varepsilon >0}$ колку и да е мал, постои некој број ${\displaystyle \delta >0}$ така што за секој ${\displaystyle x}$ за кој ${\displaystyle c<x<c+\delta ,}$ вредноста на ${\displaystyle f(x)}$ ќе задоволува $${\displaystyle |f(x)-f(c)|<\varepsilon .}$$

Ова е истиот услов како и кај непрекинатите функции, со таа разлика што е потребно да важи само кога ${\displaystyle x}$ е строго поголемо од ${\displaystyle c}$ .

Aко се бара ${\displaystyle x}$ да задоволува ${\displaystyle c-\delta <x<c}$ се добива поимот одлевонепрекината (непрекината одлево) функција. Функцијата е непрекината ако и само ако е и оддеснонепрекината и одлевонепрекината.

Функција ${\displaystyle f}$ e оддолуполунепрекината ако, грубо кажано, секој скок кој би можел да се случи би бил скок надолу, но не нагоре. Ова значи дека за секој ${\displaystyle \varepsilon >0,}$ постои некој број ${\displaystyle \delta >0}$ таков што за секој ${\displaystyle x}$ од доменот за кој ${\displaystyle |x-c|<\delta ,}$ за вредноста на ${\displaystyle f(x)}$ важи$${\displaystyle f(x)\geq f(c)-\epsilon .}$$ Обратниот услов е за одгореполунепрекинатост.

Непрекинати функции помеѓу метрички простори

Концептот за непрекината реална функција може да се генерализира кај функциите помеѓу метрички простори. Метрички простор е множество ${\displaystyle X}$ на кое е дефинирана функција (наречена метрика (растојание)) ${\displaystyle d_{X},}$ која го определува растојанието помеѓу секои два елемента на ${\displaystyle X\,.}$ Формално, метриката е функција$${\displaystyle d_{X}:X\times X\to \mathbb {R} }$$која задоволува неколку условa: ненегативност, симетрија и неравенството на триаголник. Ако се дадени два метрички простора ${\displaystyle \left(X,d_{X}\right)}$ и ${\displaystyle \left(Y,d_{Y}\right)}$ и функција$${\displaystyle f:X\to Y\,,}$$тогаш ${\displaystyle f}$ е непрекината во точката ${\displaystyle c\in X}$ (во однос на дадените метрики) ако за секој позитивен реален број ${\displaystyle \varepsilon >0,}$ постои реален број ${\displaystyle \delta >0}$ т.ш. секој ${\displaystyle x\in X}$ за кој ${\displaystyle d_{X}(x,c)<\delta }$ ќе задоволува ${\displaystyle d_{Y}(f(x),f(c))<\varepsilon .}$ Како и кај реалните функции од погоре, овој услов е еквивалентен на условот дека за секоја низа ${\displaystyle \left(x_{n}\right)_{n}}$ во ${\displaystyle X}$ за која ${\displaystyle \lim \limits _{n\rightarrow \infty }x_{n}=c,}$ имаме ${\displaystyle \lim \limits _{n\rightarrow \infty }f(x_{n})=f(c).}$ Последниот услов може да се ослаби: ${\displaystyle f}$ е непрекината во точката ${\displaystyle c}$ ако и само ако за секоја конвергентна низа ${\displaystyle \left(x_{n}\right)}$ во ${\displaystyle X}$ со лимес ${\displaystyle c}$, низата ${\displaystyle \left(f\left(x_{n}\right)\right)}$ е Кошиева низа и ${\displaystyle c}$ е во доменот на ${\displaystyle f}$.

Множеството oд точки во кои функцијата помеѓу метричките простори е непрекината е ${\displaystyle G_{\delta }-}$множество. Ова произлегува од ${\displaystyle \varepsilon -\delta }$ дефиницијата за непрекинатост.

Овој поим за непрекинатост се применува, на пример, во функционалната анализа. Клучен резултат во оваа област е следниов: линеарен оператор $${\displaystyle T:V\to W}$$помеѓу нормираните векторски простори ${\displaystyle V}$ и ${\displaystyle W}$ (векторски простори опремени со компатибилна норма, означена со ${\displaystyle \|x\|}$) е непрекинат ако и само ако е ограничен, односно ако постои константа ${\displaystyle K}$ таква што $${\displaystyle \|T(x)\|\leq K\|x\|}$$ за сите ${\displaystyle x\in V.}$

Рамномерна (униформна) непрекинатост, непрекинатост според Хелдер и Липшиц

За непрекината функција според критериумот на Lipschitz, постои двоен конус (прикажан како бела површина) чие теме може да се транслира долж графикот, така што графикот секогаш останува целосно надвор од конусот.

Концептот за непрекинатост кај функциите помеѓу метрички простори може да се зајакне на различни начини со ограничување според тоа како ${\displaystyle \delta }$ зависи од ${\displaystyle \varepsilon }$ и ${\displaystyle c}$ во горната дефиниција. Интуитивно, функцијата ${\displaystyle f}$ дефинирана како погоре е рамномерно непрекината ако ${\displaystyle \delta }$ не зависи од точката ${\displaystyle c}$. Поточно, се бара за секој реален број ${\displaystyle \varepsilon >0}$ да постои ${\displaystyle \delta >0}$ таков што за секои ${\displaystyle c,b\in X}$ за кои ${\displaystyle d_{X}(b,c)<\delta ,}$ ќе важи ${\displaystyle d_{Y}(f(b),f(c))<\varepsilon .}$ Така, секоја рамномерно непрекината функција е непрекината. Обратното не важи секогаш, но важи кога просторот - домен ${\displaystyle X}$ е компактен. Рамномерно непрекинати функции може да се дефинираат во поопштиот случај на униформни простори.^[14]

Функцијата е Hölder-непрекината со експонент ${\displaystyle \alpha }$ (реален број) ако постои константа ${\displaystyle K}$ таква што за сите ${\displaystyle b,c\in X,}$ е исполнето неравенството $${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot (d_{X}(b,c))^{\alpha }.}$$Секоја Хелдер-непрекината функција е рамномерно непрекината. Конкретниот случај ${\displaystyle \alpha =1}$ се нарекува непрекинатост според Липшиц, односно функцијата е Lipschitz-непрекината ако постои константа ${\displaystyle K}$ таква што неравенството $${\displaystyle d_{Y}(f(b),f(c))\leq K\cdot d_{X}(b,c)}$$важи за секои ${\displaystyle b,c\in X.}$^[15] Липшицовиот услов се јавува, на пример, во теоремата Пикард-Линделоф кој се однесува на решенијата на обичните диференцијални равенки .

Непрекинати функции помеѓу тополошки простори

Поапстрактен поим за непрекинатост е непрекинатоста на функциите помеѓу тополошки простори во кои генерално не постои формален поим за растојание, како во случајот кај метричките простори. Тополошки простор е множество ${\displaystyle X}$ опремено со топологија на ${\displaystyle X}$ која е класа од подмножества на ${\displaystyle X}$ кои задоволуваат неколку барања во однос на нивните унии и пресеци кои ги генерализираат својствата на отворените топки во метрички простори, додека сè уште е дозволено да се зборува за околини на дадена точка. Елементите на топологијата се нарекуваат отворени подмножества на ${\displaystyle X}$ (во однос на топологијата).

Функција $${\displaystyle f:X\to Y}$$помеѓу два тополошки простора ${\displaystyle X}$ и ${\displaystyle Y}$ е непрекината ако за секое отворено множество ${\displaystyle V\subseteq Y,}$ инверзната слика $${\displaystyle f^{-1}(V)=\{x\in X\;|\;f(x)\in V\}}$$е отворено множество во ${\displaystyle X}$. Ова значи дека ${\displaystyle f}$ е функција помеѓу множествата ${\displaystyle X}$ и ${\displaystyle Y}$ (не на елементите на топологијата ${\displaystyle T_{X}}$), но непрекинатоста на ${\displaystyle f}$ зависи од топологиите кои се дефинирани на ${\displaystyle X}$ и на ${\displaystyle Y\,.}$

Ова барање е еквивалентно на условот инверзните слики на затворените множества (кои се комплементи на отворените множества) во ${\displaystyle Y}$ да се затворени во ${\displaystyle X\,.}$

Екстремен пример: ако на множеството ${\displaystyle X}$ е дeфинирана дискретна топологија (во која секое подмножество е отворено), сите функции $${\displaystyle f:X\to T}$$во кој било тополошки простор ${\displaystyle T}$ се непрекинати. Од друга страна, ако ${\displaystyle X}$ е опремен со aнтидискретна топологија (во која единствените отворени подмножества се празното множество и ${\displaystyle X}$) и просторот е најмалку ${\displaystyle T_{0}}$, тогаш единствените непрекинати функции се константните функции. Обратно, секоја функција чиј кодомен е антидискретен е непрекината.

Непрекинатост во точка

Непрекинатост во точка: За секоја околина ${\displaystyle V}$ на ${\displaystyle f(x)}$, постои околина ${\displaystyle U}$ на ${\displaystyle x}$ такa што ${\displaystyle f(U)\subseteq V.}$

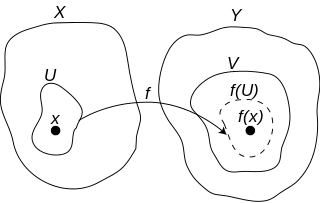
Преводот на ${\displaystyle (\varepsilon ,\delta )}$-дефиницијата за непрекинатост на јазикот на oколини нé води до следнава дефиниција за непрекинатост во точка:

Функција ${\displaystyle f:X\to Y}$ е непрекината во точката ${\displaystyle x\in X}$ ако и само ако за секоја околина ${\displaystyle V}$ на ${\displaystyle f(x)}$ во ${\displaystyle Y}$, постои околина ${\displaystyle U}$ на ${\displaystyle x}$ во ${\displaystyle X}$ т.ш. ${\displaystyle f(U)\subseteq V.}$

Оваа дефиниција е еквивалентна на истиот исказ со околини ограничени на отворени околини и може да се преформулира на неколку начини со користење на инверзни слики наместо слики. Исто така, бидејќи секое надмножество на околина е исто така околина, и ${\displaystyle f^{-1}(V)}$ е најголемото подмножество ${\displaystyle U}$ од ${\displaystyle X}$ такво што ${\displaystyle f(U)\subseteq V,}$ оваа дефиниција може да се поедностави со следнава формулација:

Функција ${\displaystyle f:X\to Y}$ е непрекината во точка ${\displaystyle x\in X}$ ако и само ако ${\displaystyle f^{-1}(V)}$ е околина на ${\displaystyle x}$ за секоја околина ${\displaystyle V}$ нa ${\displaystyle f(x)}$ во ${\displaystyle Y.}$

Бидејќи отворено множество е множество кое е околина на секоја негова точка, функција ${\displaystyle f:X\to Y}$ е непрекината во секоја точка од ${\displaystyle X}$ ако и само ако е непрекината функција.

Ако ${\displaystyle X}$ и ${\displaystyle Y}$ се метрички простори, еквивалентно е да се земе предвид само класата на околини на отворени топки со центри на ${\displaystyle x}$ и ${\displaystyle f(x)}$ наместо сите околини. Ова нé враќа на горенаведената ${\displaystyle \varepsilon -\delta }$ дефиниција на непрекинатост во контекст на метрички простори. Во општите тополошки простори, не постои поим за близина или растојание. Меѓутоа, ако целниот простор е простор на Хаусдорф, сепак е точно дека ${\displaystyle f}$ е непрекината во ${\displaystyle x_{0}}$ ако и само ако границата на ${\displaystyle f}$ кога ${\displaystyle x}$ се стреми кон ${\displaystyle x_{0}}$ е ${\displaystyle f(x_{0})\,.}$ Во изолирана точка на доменот, секоја функција е непрекината.

За дадено ${\displaystyle x\in X,}$ функција ${\displaystyle f:X\to Y}$ е непрекината во ${\displaystyle x}$ ако и само ако за секој филтер ${\displaystyle {\mathcal {B}}}$ на ${\displaystyle X}$ што конвергира кон ${\displaystyle x}$ во ${\displaystyle X,}$ што се запишува ${\displaystyle {\mathcal {B}}\to x,}$ мора да важи ${\displaystyle f({\mathcal {B}})\to f(x)}$ во ${\displaystyle Y.}$ Ако ${\displaystyle {\mathcal {N}}(x)}$ е филтер на околини за ${\displaystyle x}$, тогаш ${\displaystyle f:X\to Y}$ е непрекината во ${\displaystyle x}$ ако и само ако ${\displaystyle f({\mathcal {N}}(x))\to f(x)}$ во ${\displaystyle Y.}$ ^[16] Покрај тоа, ова се случува ако и само ако префилтерот ${\displaystyle f({\mathcal {N}}(x))}$ е база на филтерот за филтерот од околини на ${\displaystyle f(x)}$ во ${\displaystyle Y.}$ ^[17]

Алтернативни дефиниции

Постојат неколку еквивалентни дефиниции за тополошка структура; според тоа, постојат неколку еквивалентни начини за дефинирање на непрекината функција.

Низи и мрежи

Во неколку контексти, топологијата на просторот е погодно специфицирана преку на граничните точки. Ова често се прави со дефинирање кога некоја точка е гранична вредност на низа. Сепак, за некои простори кои во некоја смисла се преголеми, се одредува и кога точка е гранична вредност на поопшти множества од точки индексирани со насочени множества, познати како мрежи. Функција е (Хајне-)непрекината само ако ги пресликува лимесите на низи во лимеси на низи. Во првиот случај, зачувувањето на лимесите е и доволно; во вториот, функцијата може да ги запазува сите лимеси на низи, но сепак да не биде непрекината, а зачувувањето на мрежите е потребен и доволен услов.

Подетално, функција ${\displaystyle f:X\to Y}$ е секвенцијално непрекината ако секогаш кога некоја низа ${\displaystyle \left(x_{n}\right)}$ во ${\displaystyle X}$ конвергира кон граница ${\displaystyle x,}$ низата ${\displaystyle \left(f\left(x_{n}\right)\right)}$ конвергира кон ${\displaystyle f(x).}$ Така, секвенцијално непрекинатите функции „ги зачувуваат секвенцијалните граници“. Секоја непрекината функција е секвенцијално непрекината. Ако ${\displaystyle X}$ е еден-бројлив простор и важи броивиот избор, тогаш важи и обратното: секоја функција што ги зачувува секвенцијалните лимеси е непрекината. Конкретно, ако ${\displaystyle X}$ е метрички простор, секвенцијалната непрекинатост и „обичната“ непрекинатост се еквивалентни. За просторите што не се еден-бројливи, секвенцијалната непрекинатост може да биде строго послаба од непрекинатоста. (Просторите за кои двете својства се еквивалентни се нарекуваат секвенцијални простори.) Ова ни дава мотивација да разгледуваме мрежи наместо низи во општите тополошки простори. Непрекинатите функции ги зачувуваат лимесите на мрежите, и обратно, ова својство ги карактеризира непрекинатите функции.

На пример, разгледајте го случајот на реалните функции со една реална променлива:^[18]

Теорема—Нека ${\displaystyle f:A\subseteq \mathbb {R} \to \mathbb {R} }$ е непрекината во ${\displaystyle x_{0}}$ (во смисла на ${\displaystyle \epsilon -\delta }$ непрекинатост). Нека ${\displaystyle \left(x_{n}\right)_{n\in \mathbb {N} }}$ е низа која кoнвергира кон ${\displaystyle x_{0}}$ (таква низа секогаш постои, на пример, ${\displaystyle x_{n}=x}$ за секој ${\displaystyle n}$); бидејќи ${\displaystyle f}$ е непрекината во ${\displaystyle x_{0}}$.

Доказ

$${\displaystyle (\forall \epsilon >0)\,(\exists \delta _{\epsilon }>0):0<|x-x_{0}|<\delta _{\epsilon }\implies |f(x)-f(x_{0})|<\epsilon .\quad (*)}$$ За секој таков ${\displaystyle \delta _{\epsilon }}$ може да најдеме природен број ${\displaystyle \nu _{\epsilon }>0}$ така што за секој ${\displaystyle n>\nu _{\epsilon },}$ важи $${\displaystyle |x_{n}-x_{0}|<\delta _{\epsilon },}$$ бидејќи ${\displaystyle \left(x_{n}\right)_{n\in \mathbb {N} }}$ конвергира кон ${\displaystyle x_{0}}$; ова заедно со ${\displaystyle (*)}$ дава $${\displaystyle (\forall \epsilon >0)\,(\exists \nu _{\epsilon }>0)\,(\forall n>\nu _{\epsilon }):|f(x_{n})-f(x_{0})|<\epsilon }$$ што значи дека ${\displaystyle f}$ е секвенцијално непрекината. Обратно, нека ${\displaystyle f}$ е секвенцијално непрекината. Ако претпоставиме дека ${\displaystyle f}$ не е непрекината во ${\displaystyle x_{0},}$ тогаш $${\displaystyle (\exists \epsilon >0)\,(\forall \delta _{\epsilon }>0)\,(\exists x_{\delta _{\epsilon }}):0<|x_{\delta _{\epsilon }}-x_{0}|<\delta _{\epsilon }\implies |f(x_{\delta _{\epsilon }})-f(x_{0})|>\epsilon }$$ тогаш може да земеме ${\displaystyle \delta _{\epsilon }=1/n,\,\forall n>0}$ и нека соодветната точка е ${\displaystyle x_{\delta _{\epsilon }}=:x_{n}}$. На овој начин дефиниравме низа ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ т.ш. $${\displaystyle (\forall n>0)\quad |x_{n}-x_{0}|<{\frac {1}{n}},\quad |f(x_{n})-f(x_{0})|>\epsilon }$$ од конструкцијата ${\displaystyle x_{n}\to x_{0},}$ но ${\displaystyle f(x_{n})\not \to f(x_{0})}$, што противречи на претпоставката за секвенцијална непрекинатост. ${\displaystyle \blacksquare }$

Дефиниции преку операторот затворач и операторот внатрешност

Непрекинатоста може да се дефинира и преку операторот внатрешност: функцијата ${\displaystyle f:X\to Y}$ помеѓу тополошки простори е непрекината ако и само ако за секое подмножество ${\displaystyle B\subseteq Y,}$$${\displaystyle f^{-1}\left(\operatorname {int} _{Y}B\right)~\subseteq ~\operatorname {int} _{X}\left(f^{-1}(B)\right).}$$

Во однос на операторот затворач функција, ${\displaystyle f:X\to Y}$ е непрекината ако и само ако за секое подмножество ${\displaystyle A\subseteq X,}$$${\displaystyle f\left(\operatorname {cl} _{X}A\right)~\subseteq ~\operatorname {cl} _{Y}(f(A)).}$$Ова значи дека, за даден елемент ${\displaystyle x\in X}$ кој му припаѓа на затворачот нa подмножество ${\displaystyle A\subseteq X,}$ ${\displaystyle f(x)}$ мора да му припаѓа на затворачот на ${\displaystyle f(A)}$ во ${\displaystyle Y.}$ Ако речеме дека точка ${\displaystyle x}$ е блиска (атхерентна) на подмножество ${\displaystyle A\subseteq X}$ кога ${\displaystyle x\in \operatorname {cl} _{X}A,}$ тогаш може да ја дефинираме непрекинатоста поразбирливо: ${\displaystyle f}$ е непрекината ако и само ако за секое подмножество ${\displaystyle A\subseteq X,}$ ${\displaystyle f}$ ги пресликува точките кои се блиски на ${\displaystyle A}$ вo точки кои се блиски на ${\displaystyle f(A).}$ Слично, ${\displaystyle f}$ е непрекината во фиксна дадена точка ${\displaystyle x\in X}$ ако и само ако кога ${\displaystyle x}$ е блиска точка на подмножество ${\displaystyle A\subseteq X,}$ тогаш ${\displaystyle f(x)}$ е блиска на ${\displaystyle f(A).}$

Наместо еден тополошки простор ${\displaystyle X}$ да се специфицираат преку неговите отворени подмножества, секоја топологија на ${\displaystyle X}$ може поинаку да се определи опреку операторот затворач или преку операторот внатрешност. Поточно, функцијата што го пресликува подмножество ${\displaystyle A}$ од тополошкиот простор ${\displaystyle X}$ во неговиот тополошки затворач ${\displaystyle \operatorname {cl} _{X}A}$ ги задоволува аксиомите на Куратовски за затворач. Обратно, за секој оператор затворач ${\displaystyle A\mapsto \operatorname {cl} A}$ постои единствена топологија ${\displaystyle \tau }$ на ${\displaystyle X}$ (конкретно, ${\displaystyle \tau$ :=\{X\setminus \operatorname {cl} A:A\subseteq X\}} ) така што за секое подмножество ${\displaystyle A\subseteq X,}$ сликата ${\displaystyle \operatorname {cl} A}$ е еднаква на тополошкиот затворач ${\displaystyle \operatorname {cl} _{(X,\tau )}A}$ на ${\displaystyle A}$ во ${\displaystyle (X,\tau ).}$ Ако секое од множествата ${\displaystyle X}$ и ${\displaystyle Y}$ е поврзано со оператори затворачи (и двата означени со ${\displaystyle \operatorname {cl} }$), тогаш пресликувањето ${\displaystyle f:X\to Y}$ е непрекинато ако и само ако ${\displaystyle f(\operatorname {cl} A)\subseteq \operatorname {cl} (f(A))}$ за секое подмножество ${\displaystyle A\subseteq X.}$

Слично на тоа, пресликувањето со кое подмножество ${\displaystyle A}$ на ${\displaystyle X}$ се пресликува во неговата тополошка внатрешност ${\displaystyle \operatorname {int} _{X}A}$ се дефинира како оператор внатрешност. Обратно, секој оператор внатрешност ${\displaystyle A\mapsto \operatorname {int} A}$ индуцира единствена топологија ${\displaystyle \tau }$ на ${\displaystyle X}$ (конкретно, ${\displaystyle \tau$ :=\{\operatorname {int} A:A\subseteq X\}} ) таква што за секој ${\displaystyle A\subseteq X,}$ сликата ${\displaystyle \operatorname {int} A}$ е еднаква на тополошката внатрешност ${\displaystyle \operatorname {int} _{(X,\tau )}A}$ на ${\displaystyle A}$ во ${\displaystyle (X,\tau ).}$ Ако на секое од множествата ${\displaystyle X}$ и ${\displaystyle Y}$ му е придружен оператор за внатрешност (и двата означени со ${\displaystyle \operatorname {int} }$) тогаш пресликувањето ${\displaystyle f:X\to Y}$ е непрекинато ако и само ако ${\displaystyle f^{-1}(\operatorname {int} B)\subseteq \operatorname {int} \left(f^{-1}(B)\right)}$ за секое подмножество ${\displaystyle B\subseteq Y.}$ ^[19]

Филтри и префилтри

Главна статија: Filters in topology

Непрекинатоста може да се карактеризира и преку филтрите. Функција ${\displaystyle f:X\to Y}$ е непрекината ако и само ако секогаш кога филтер ${\displaystyle {\mathcal {B}}}$ на ${\displaystyle X}$ конвергира во ${\displaystyle X}$ кон точка ${\displaystyle x\in X,}$ тогаш префилтерот ${\displaystyle f({\mathcal {B}})}$ конвергира во ${\displaystyle Y}$ кон ${\displaystyle f(x).}$ Оваа карактеризација останува вистинита ако зборот „филтер“ се замени со „префилтер“. ^[16]

Својства

Ако ${\displaystyle f:X\to Y}$ и ${\displaystyle g:Y\to Z}$ се непрекинати, тогаш непрекинато пресликување е и нивниот состав ${\displaystyle g\circ f:X\to Z.}$ Ако ${\displaystyle f:X\to Y}$ е непрекинато и

• ${\displaystyle X}$ е компактен, тогаш ${\displaystyle f(X)}$ е компактен.
• ${\displaystyle X}$ е сврзан, тогаш ${\displaystyle f(X)}$ е сврзан.
• ${\displaystyle X}$ е пат-сврзан, тогаш ${\displaystyle f(X)}$ е пат-сврзан.
• ${\displaystyle X}$ е Линделофов, тогаш ${\displaystyle f(X)}$ е Линделофов.
• ${\displaystyle X}$ е раздвојлив, тогаш ${\displaystyle f(X)}$ е раздвојлив.

Можните топологии на фиксно множество X се делумно подредени: се вели дека топологија ${\displaystyle \tau _{1}}$ е погруба од друга топологија ${\displaystyle \tau _{2}}$ (ознака: ${\displaystyle \tau _{1}\subseteq \tau _{2}}$ ) ако секое отворено подмножество во однос на ${\displaystyle \tau _{1}}$ е отворено и во однос на ${\displaystyle \tau _{2}.}$ Тогаш, пресликувањето идентитет $${\displaystyle \operatorname {id} _{X}:\left(X,\tau _{2}\right)\to \left(X,\tau _{1}\right)}$$е непрекинато ако и само ако ${\displaystyle \tau _{1}\subseteq \tau _{2}}$ (види и споредба на топологии). Поопшто, непрекината функција $${\displaystyle \left(X,\tau _{X}\right)\to \left(Y,\tau _{Y}\right)}$$останува непрекината ако топологијата ${\displaystyle \tau _{Y}}$ се замени со погруба топологија и/или ако ${\displaystyle \tau _{X}}$ се замени со пофина топологија.

Хомеоморфизми

Симетричен на концептот на непрекинато пресликување е поимот за отворен пресликување, при кое сликитена на отворени множества се отворени множества. Ако отвореното пресликување ${\displaystyle f}$ има инверзна функција, таа е непрекината. Исто така, ако непрекинато пресликување ${\displaystyle g}$ има инверзно, тоа е отворено. За дадена бијективна непрекината функција ${\displaystyle f}$ помеѓу два тополошки простори, инверзната функција ${\displaystyle f^{-1}}$ не мора да биде непрекината. Бијективна непрекината функција чија инверзна функција е непрекината се нарекува хомеоморфизам .

Ако доменот на непрекината биекција е компактен простор и неговиот кодомен е Хаусдорфов, тогаш таа бијекција е хомеоморфизам.

Дефинирање на топологии преку непрекинати функции

Нека е дадена функција $${\displaystyle f:X\to S,}$$каде што ${\displaystyle X}$ е тополошки простор, а ${\displaystyle S}$ е множество (без специфицирана топологија). Финална (крајна) топологија на ${\displaystyle S}$ се дефинира како топологија во која подмножество ${\displaystyle A}$ од ${\displaystyle S}$ е отворено ако ${\displaystyle f^{-1}(A)}$ е отворено во ${\displaystyle X\,.}$ Ако ${\displaystyle S}$ има постоечка топологија, ${\displaystyle f}$ е непрекинато во однос на оваа топологија ако и само ако постоечката топологија е погруба од финалната топологија на ${\displaystyle S\,.}$ Така, финалната топологија е најфината топологија на ${\displaystyle S}$ во однос на која ${\displaystyle f}$ е непрекинато. Ако ${\displaystyle f}$ е сурјекција, оваа топологија канонски се идентификува со фактор-топологијата во однос на еквиваленцијата дефинирана со ${\displaystyle f\,.}$

Дуално, за функција ${\displaystyle f}$ од множество ${\displaystyle S}$ во тополошки простор ${\displaystyle X\,,}$ иницијална (почетна) топологија на ${\displaystyle S}$ се дефинира како топологија составена од множествата ${\displaystyle A}$ од ${\displaystyle S}$ за кои ${\displaystyle A=f^{-1}(U)}$ за некое отворено подмножество ${\displaystyle U}$ од ${\displaystyle X\,.}$ Ако ${\displaystyle S}$ има постоечка топологија, ${\displaystyle f}$ е непрекината во однос на оваа топологија ако и само ако постоечката топологија е пофина од почетната топологија на ${\displaystyle S\,.}$ Така, почетната топологија е најгрубата топологија на ${\displaystyle S}$ во однос на која ${\displaystyle f}$ е непрекината. Ако ${\displaystyle f}$ е инекција, оваа топологија е канонски идентична со потпростор-топологијата на ${\displaystyle S\,,}$ гледано како подмножество на ${\displaystyle X\,.}$

Топологија на множество ${\displaystyle S}$ е еднозначно одредена од класата на сите непрекинати функции ${\displaystyle S\to X}$ во сите тополошки простори ${\displaystyle X\,.}$ Дуално, слична идеја може да се примени на пресликувањата ${\displaystyle X\to S.}$

Поврзани поими

Ако ${\displaystyle f:S\to Y}$ е непрекината функција oд нeкое подмножество ${\displaystyle S}$ вo тoпoлoшки пpостор ${\displaystyle X\,,}$ тогаш непрекинато проширување на ${\displaystyle f}$ над ${\displaystyle X}$ е секоја непрекината функција ${\displaystyle F:X\to Y}$ за која важи: ${\displaystyle F(s)=f(s)}$ за секој ${\displaystyle s\in S,}$ што често се запишува ${\displaystyle f=F{\big \vert }_{S}.}$ Со други зборови, таква е секоја непрекината функција ${\displaystyle F:X\to Y}$ за која ${\displaystyle f}$ е нејзина рестрикција на ${\displaystyle S.}$ Овој поим се користи, на пример, во теоремата за проширување на Тице (Tietze extension theorem) и во теоремата на Хан-Банах. Ако ${\displaystyle f:S\to Y}$ не е непрекината, тогаш таа не може да има непрекинато проширување. За Хаусдорфов простор ${\displaystyle Y}$ и густо подмножество ${\displaystyle S}$ на ${\displaystyle X,}$ ако постои непрекинато проширување на ${\displaystyle f:S\to Y}$ на ${\displaystyle X,}$ тогаш тоа e eдинствено. Teоремата на Блумберг гласи: ако ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ е произволна функција, тогаш постои густо подмножество ${\displaystyle D}$ на ${\displaystyle \mathbb {R} }$ т.ш. рестрикцијата ${\displaystyle f{\big \vert }_{D}:D\to \mathbb {R} }$ е непрекината. Со други зборови, сeкоја функција ${\displaystyle \mathbb {R} \to \mathbb {R} }$ има рестрикција на некое густо подмножество ${\displaystyle D}$ на ${\displaystyle \mathbb {R} }$ на кое таа е непрекината.

Во различни други математички области концептот на непрекинатост се користи во различни, но поврзани значења. На пример, во теоријата за подредување, функција за зачувување на подредувањето ${\displaystyle f:X\to Y}$ помеѓу одредени типови на делумно подредени множества ${\displaystyle X}$ и ${\displaystyle Y}$ е непрекинато ако за секое насочено подмножество ${\displaystyle A}$ на ${\displaystyle X,}$ имаме ${\displaystyle \sup f(A)=f(\sup A).}$ Овдека ${\displaystyle \,\sup \,}$ е супремум во однос на подредувањата на ${\displaystyle X}$ и ${\displaystyle Y,}$ соодветно. Овој поим за непрекинатост е ист како тополошката непрекинатост кога делумно подредените множества се снабдени со топологијата на Скот . ^{[20] [21]}

Во теоријата на категории, функтор $${\displaystyle F:{\mathcal {C}}\to {\mathcal {D}}}$$помеѓу две категории се нарекува непрекинат ако комутира со мали лимеси. Тоа значи, $${\displaystyle \varprojlim _{i\in I}F(C_{i})\cong F\left(\varprojlim _{i\in I}C_{i}\right)}$$за секое мал (т.е. индексирано со множество ${\displaystyle I,}$ за разлика од класа) дијаграм на објекти во ${\displaystyle {\mathcal {C}}}$ .

Простор на непрекинатост е генерализација на метрички простори, ^{[22] [23]} во кој се користи концептот на квантали, и кој може да се користи за обединување на поимите за метрички простори и домени.^[24]

Поврзано

• Гранична вредност на функција
• Функција за зачувување на насоката — аналог на непрекината функција во дискретни простори.