Funkcja różnowartościowa

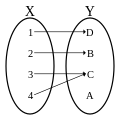
Funkcja różnowartościowa, iniekcja^[1] (injekcja), funkcja 1-1 ^[2]– funkcja, której każdy element przeciwdziedziny przyjmowany jest co najwyżej raz. Funkcja ${\displaystyle f\colon X\to Y}$ jest różnowartościowa wtedy i tylko wtedy, gdy dla dowolnych dwóch elementów ${\displaystyle a,b\in X}$ spełniony jest warunek^[3]:

${\displaystyle a\neq b\Rightarrow f(a)\neq f(b).}$

Diagram przemienny przedstawiający iniekcję jako funkcję odwracalną lewostronnie

Złożenie dwóch funkcji iniekcyjnych również jest iniekcją^{[potrzebny przypis]}

Stosuje się także równoważną postać powyższej implikacji (powstałą przez kontrapozycję):

${\displaystyle f(a)=f(b)\Rightarrow a=b.}$

Warunki równoważne:^{[potrzebny przypis]}:

• przeciwobraz singletonu ma co najwyżej jeden element;
• istnieje lewostronna funkcja odwrotna: ${\displaystyle g\circ f=\mathrm {id_{X}} .}$

Termin iniekcja powstał najpóźniej w 1950 roku, kiedy to Saunders Mac Lane użył go w jednym z amerykańskich czasopism matematycznych^[4].

• 
  Iniekcyjna funkcja niesurjekcyjna (iniekcja, nie bijekcja)
• 
  Iniekcyjna surjekcyjna funkcja (bijekcja)
• 
  Nieinjekcyjna surjekcyjna funkcja (surjekcja, nie bijekcja)
• 
  Nieinjekcyjna niesurjekcyjna funkcja (również nie bijekcja)

Przykłady i własności

• numer PESEL – funkcja przypisująca osobie jej numer PESEL jest iniekcją - dwie osoby nie mogą mieć jednakowego numer PESEL;
• transliteracje to iniekcje między zbiorami ciągów (krotek) znaków. Niektóre transliteracje są też iniekcjami między zbiorami samych znaków^{[potrzebny przypis]};
• pierwiastek dowolnego stopnia naturalnego;
• funkcja wykładnicza zmiennej rzeczywistej; przyjmuje wyłącznie wartości nieujemne, przez co nie jest „na” przy takiej samej przeciwdziedzinie;
• funkcje kołowe;
• dowolna inna funkcja ściśle monotoniczna (ściśle rosnąca lub ściśle malejąca);
• negacja na zbiorze zdań oznajmujących danego języka;
• wszelkie bijekcje.

Wprost z definicji wynika, że iniekcja nie może być funkcją parzystą (jeśli jej dziedzina zawiera jakąkolwiek niezerową wartość) ani okresową, ponieważ własności te są zdefiniowane przez równość wartości dla różnych argumentów. Iniekcjami nie są również:

• wielomiany rzeczywiste stopnia parzystego, nawet jeśli nie są funkcjami parzystymi; np. ${\displaystyle (x-1)^{4}}$ , przy czym możliwe jest zawężenie dziedziny wielomianiu, tak by był on iniekcją, ale tylko jako funkcja okreslona na zawężonej dziedzinie (np wielomian ${\displaystyle (x-1)^{4}}$ jest iniekcją na zbiorze liczb większych od 1).
• funkcja Collatza – jest sumą mnogościową iniekcji na zbiorach liczb parzystych i nieparzystych, jednak dla argumentu parzystego i nieparzystego może przyjąć jednakową wartość. Przykładowo ${\displaystyle c(3)=c(20)=10.}$

Zobacz też

• monomorfizm
• twierdzenie Cantora-Bernsteina-Schrödera – o konsekwencji istnienia pewnych iniekcji
• zasada szufladkowa Dirichleta – fakt nieistnienia pewnych iniekcji