Przeciwobraz

Przeciwobraz zbioru – pojęcie matematyczne, konkretniej teorii mnogości, związane z dowolną funkcją lub inną relacją dwuargumentową^[1]. Przeciwobrazy definiuje się dla podzbiorów przeciwdziedziny – dla funkcji ${\displaystyle f\colon X\to Y}$ przeciwobrazy dotyczą dowolnego zbioru ${\displaystyle B\subseteq Y}$. Przeciwobraz zbioru ${\displaystyle B}$ to zbiór wszystkich elementów dziedziny, które są odwzorowane na elementy ${\displaystyle B}$^[2].

Diagram przykładowej funkcji. Przeciwobrazem elementu ${\displaystyle a}$ jest jedynka ${\displaystyle \{1\},}$ przeciwobrazem elementu ${\displaystyle b}$ – zbiór dwuelementowy dwójki i trójki ${\displaystyle \{2;\ 3\},}$ a przeciwobrazy elementów ${\displaystyle c}$ i ${\displaystyle d}$ są puste ${\displaystyle (\emptyset ).}$

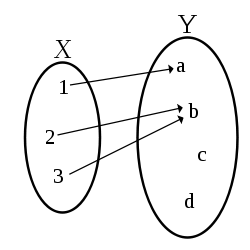
Pojęcie przeciwobrazu bywa używane w różnych działach matematyki, nie tylko wyższej; przeciwobrazami można definiować inne pojęcia jak miejsce zerowe^[3] i funkcja ciągła^[4].

Przeciwobraz względem funkcji

Definicje i zapis

Niech ${\displaystyle f\colon X\to Y}$ oznacza dowolną funkcję ze zbioru ${\displaystyle X}$ w zbiór ${\displaystyle Y}$. Przeciwobrazem zbioru ${\displaystyle B\subseteq Y}$ względem ${\displaystyle f}$ nazywa się podzbiór zbioru ${\displaystyle X}$ określony wzorem

${\displaystyle f^{-1}[B]=\{x\in X\colon f(x)\in B\}.}$

Inne oznaczenia^[2][5]:

• ${\displaystyle f^{-1}(B);}$
• ${\displaystyle {\vec {f}}^{-1}(B).}$

Przeciwobraz względem ustalonej funkcji ${\displaystyle f}$, oznaczany ${\displaystyle {\vec {f}}^{-1}}$, to funkcja ze zbioru potęgowego zbioru ${\displaystyle Y}$ w zbiór potęgowy zbioru ${\displaystyle X}$, czyli ${\displaystyle {\vec {f}}^{-1}:2^{Y}\rightarrow 2^{X}}$^[5][6].

Symbol ${\displaystyle f^{-1}}$ stosuje się do funkcji odwrotnych, które są odrębnym pojęciem. Ono pokrywa się z przeciwobrazem wtedy i tylko wtedy, gdy ${\displaystyle f}$ jest bijekcją^{[potrzebny przypis]}.

Przykłady

Niech funkcja rzeczywista ${\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {R} }$ będzie dana wzorem ${\displaystyle f(x,y)=x^{2}+y^{2}.}$ Przeciwobraz liczby rzeczywistej ${\displaystyle a}$ przy tej funkcji – oznaczany ${\displaystyle f^{-1}(a)}$ – zależy od jej wartości^[3]:

• dla ${\displaystyle a>0}$ przeciwobrazami są okręgi o wspólnym środku w początku układu współrzędnych;
• dla ${\displaystyle a=0}$ przeciwobrazem jest sam początek układu;
• dla ${\displaystyle a<0}$ przeciwobrazem jest zbiór pusty.

Własności

Istnieją ogólne związki przeciwobrazu z działaniami na zbiorach takimi jak suma ${\displaystyle (\cup ),}$ przekrój ${\displaystyle (\cap )}$ i różnica ${\displaystyle (\backslash ).}$ Jeśli ${\displaystyle B,B_{1},B_{2}\subseteq Y,}$ to^[7][5]:

• ${\displaystyle f^{-1}[B_{1}\cup B_{2}]=f^{-1}[B_{1}]\cup f^{-1}[B_{2}];}$
• ${\displaystyle f^{-1}[B_{1}\cap B_{2}]=f^{-1}[B_{1}]\cap f^{-1}[B_{2}];}$
• ${\displaystyle f^{-1}[Y\backslash B]=f^{-1}[Y]\backslash f^{-1}[B].}$

Istnieją też ogólne związki z pojęciem obrazu zbioru^[7]:

• obraz przeciwobrazu to podzbiór wyjściowego zbioru: ${\displaystyle f[f^{-1}[B]]\subseteq B.}$ Równość zachodzi dla funkcji „na” (suriekcji);
• przeciwobraz obrazu to nadzbiór wyjściowego zbioru: ${\displaystyle f^{-1}[f[A]]\supseteq A.}$ Równość zachodzi dla funkcji różnowartościowych (iniekcji)^[8][9].

Włókna

Przeciwobraz zbioru jednoelementowego oznacza się ${\displaystyle \textstyle f^{-1}[\scriptstyle \{y\}\textstyle ]}$ lub krócej ${\displaystyle f^{-1}[y].}$ Nazywa się go włóknem nad ${\displaystyle y}$, poziomicą^[3] lub warstwicą ${\displaystyle y}$^{[potrzebny przypis]}.

Zbiór wszystkich włókien nad elementami ${\displaystyle Y}$ tworzy rodzinę zbiorów indeksowaną przez ${\displaystyle Y.}$ Prowadzi to do pojęcia kategorii rozwłóknień^{[potrzebny przypis]}.