Пятиугольная мозаика порядка 4

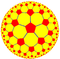
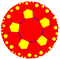
Пятиугольная мозаика порядка 4 — это правильная мозаика на гиперболической плоскости. Мозаика представлена символом Шлефли {5,4}. Мозаика может быть названа пятипятиугольной мозаикой, если представлена в двуцветном квазиправильном виде.

Пятиугольная мозаика порядка 4
Тип	Правильная гиперболическая мозаика
Конфигурация вершины	54
Символ Шлефли	{5,4} r{5,5} or ${\displaystyle {\begin{Bmatrix}5\\5\end{Bmatrix}}}$
Символ Витхоффа	4 | 5 2 2 | 5 5
Симметрии	[5,4], (*542) [5,5], (*552)
Диаграммы Коксетера — Дынкина	или
Двойственные соты	Квадратная мозаика порядка 5[англ.]
Свойства	Изогональная, изотоксальная, изоэдральная

Симметрия

Эта мозаика представляет гиперболический калейдоскоп из пяти зеркал, находящихся на краях правильного пятиугольника. Такая симметрия в орбифолдной нотации^[англ.] имеет название *22222 и имеет 5 пересечений зеркал порядка 2.

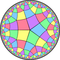
Калейдоскопную область можно рассматривать как выкрашенные в два цвета пятиугольники, представляющие зеркальные образа фундаментальной области. Такая раскраска представляет однородную мозаику t₁{5,5} и, являясь квазиправильной мозаикой, называется пятипятиугольной мозаика.

Связанные многогранники и мозаики

Однородные пятиугольные/квадратные мозаики
Симметрия: [5,4], (*542)							[5,4]+, (542)	[5+,4], (5*2)	[5,4,1+], (*552)
{5,4}	t{5,4}	r{5,4}	2t{5,4}=t{4,5}	2r{5,4}={4,5}	rr{5,4}	tr{5,4}	sr{5,4}	s{5,4}	h{4,5}
Однородные двойственные
V54	V4.10.10	V4.5.4.5	V5.8.8	V45	V4.4.5.4	V4.8.10	V3.3.4.3.5	V3.3.5.3.5	V55

Однородные пятипятиугольные мозаики
Симметрия: [5,5], (*552)							[5,5]+, (552)
=	=	=	=	=	=	=	=
{5,5}	t{5,5}	r{5,5}	2t{5,5}=t{5,5}	2r{5,5}={5,5}	rr{5,5}	tr{5,5}	sr{5,5}
Однородные двойственные duals
V5.5.5.5.5	V5.10.10	V5.5.5.5	V5.10.10	V5.5.5.5.5	V4.5.4.5	V4.10.10	V3.3.5.3.5

Мозаика топологически является частью последовательности правильных многогранников и мозаик с пятиугольными гранями. Последовательность начинается с додекаэдра, имеет символ Шлефли {5,n} и диаграмму Коксетера и продолжается до бесконечности.

мозаики {5,n}
{5,3}	{5,4}	{5,5}	{5,6}	{5,7}

Мозаика также топологически является частью последовательности правильных многогранников и мозаик с четырьмя гранями на вершину. Последовательность начинается с октаэдра, имеет символ Шлефли {n,4} и диаграмму Коксетера и продолжается до бесконечности.

Варианты симметрии *n42 правильных мозаик {n,4}
Сферические		Евклидовы	Гиперболические мозаики
24	34	44	54	64	74	84	...∞4

Мозаика топологически является частью последовательности правильных многогранников и мозаик с вершинно фигурой (4ⁿ).

Варианты симметрии *n42 правильных мозаик: {4,n}
Сферические	Евклидовы	Компактные гиперболические				Паракомпактные
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4,∞}

Варианты симметрии *5n2 квазиправильных мозаик: (5.n)2
Симметрия *5n2 [n,5]	Сферические	Гиперболические					Паракомпактные	Компактные
	*352 [3,5]	*452 [4,5]	*552 [5,5]	*652 [6,5]	*752 [7,5]	*852 [8,5]...	*∞52 [∞,5]	[ni,5]
Изображения
Конфиг.	(5.3)2	(5.4)2	(5.5)2	(5.6)2[англ.]	(5.7)2	(5.8)2	(5.∞)2	(5.ni)2
Ромбические фигуры
Конфиг.	V(5.3)2	V(5.4)2	V(5.5)2[англ.]	V(5.6)2	V(5.7)2	V(5.8)2	V(5.∞)2	V(5.∞)2

См. также

• Квадратный паркет
• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на плоскости^[англ.]
• Список правильных многомерных многогранников и соединений