சமபக்க முக்கோணி
From Wikipedia, the free encyclopedia
Remove ads
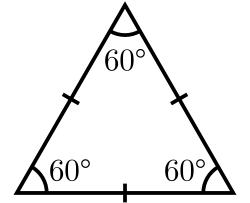
சமபக்க முக்கோணி அல்லது சமபக்க முக்கோணம் (Equilateral Triangle) என்பது மூன்று பக்கங்களும் சமமாக உள்ள முக்கோணம் ஆகும்.[1] எந்தவொரு முக்கோணியினதும் அகக்கோணங்களின் கூட்டுத்தொகையானது 180° ஆக இருக்கும்.[2] ஆகவே, எந்தவொரு சமபக்க முக்கோணத்தின் அகக்கோணங்களின் கூட்டுத்தொகையும் 180° ஆகவே இருக்கும்.
சமபக்க முக்கோணியொன்றின் அகக்கோணமொன்று 60° ஆகவும் புறக்கோணமொன்று 120° ஆகவும் இருக்கும்.[3]
Remove ads
முதன்மை இயல்புகள்

- சமபக்க முக்கோணத்தின் பரப்பளவு ஆகும்.[4]
- சமபக்க முக்கோணத்தின் சுற்றளவு ஆகும்.[5]
- சமபக்க முக்கோணத்தின் சுற்றுவட்டத்தின் ஆரை ஆகும்.
- சமபக்க முக்கோணத்தின் உள்வட்டத்தின் ஆரை ஆகும்.
- சமபக்க முக்கோணத்தின் மையமே அதனுடைய உள்வட்டம், சுற்றுவட்டம் என்பனவற்றின் மையமாக இருக்கும்.
- எந்தப் பக்கத்திலிருந்தும் சமபக்க முக்கோணத்தின் செங்குத்துயரம் ஆகும்.[6]
சமபக்க முக்கோணத்தின் உயரத்தின் மூலமாக மேலுள்ள வாய்ப்பாடுகள்:
- சமபக்க முக்கோணத்தின் பரப்பளவு
- சமபக்க முக்கோணத்தின் மூன்று பக்கங்களிலிருந்தும் அதன் மையத்தின் உயரம்
- சுற்றுவட்ட ஆரம்
- உள்வட்ட ஆரம்
ஒரு சமபக்க முக்கோணத்தின் குத்துக்கோடுகள், பக்கங்களின் நடுக்குத்துக்கோடுகள், கோண இருசமவெட்டிகள், இடைக்கோடுகள் ஒன்றோடொன்று பொருந்தும்.
Remove ads
பண்புருக்கள்
ஒரு முக்கோணத்தில் வழமையான குறியீடுகள்: முக்கோணம் ABC இன் பக்கங்கள் a, b, c, அரைச்சுற்றளவு s, பரப்பளவு T, வெளிவட்ட ஆரங்கள் ra, rb, rc, சுற்றுவட்ட ஆரம் R , உள்வட்ட ஆரம் r .
கீழே தரப்பட்டுள்ள ஒன்பது வகைகளில் ஏதேனும் ஒன்று உண்மையாக ‘இருந்தால், இருந்தால் மட்டுமே’, ஒரு முக்கோணம் சமபக்க முக்கோணமாக இருக்கும். எனவே இவை ஒவ்வொன்றும் சமபக்க முக்கோணத்தின் தனிப்பட்ட பண்புகளாகும்.
பக்கங்கள்
அரைச்சுற்றளவு
கோணங்கள்
பரப்பளவு
சுற்றுவட்ட ஆரம், உள்வட்ட ஆரம், வெளிவட்ட ஆரங்கள்
சம விழுகோடுகள்
சமபக்க முக்கோணங்களில் (மட்டும்) மூன்று வகை விழுகோடுகள் சமநீளமானவை:[14]
- மூன்று குத்துக்கோடுகள் சமநீளமுள்ளவை.
- மூன்று நடுக்கோடுகள் சமநீளமுள்ளவை
- மூன்று கோண இருசமவெட்டிகள் சம நீளமுள்ளவை.
ஒன்றுபடும் முக்கோண மையங்கள்
சமபக்க முக்கோணத்தின் ஒவ்வொரு முக்கோண மையங்களும் அம்முக்கோணத்தின் நடுக்கோட்டுச்சந்தியுடன் ஒன்றுபடும்.
ஒரு முக்கோணத்தின் சில முக்கோண மையச்சோடிகள் ஒன்றுபடுகின்றன என்ற கூற்றே அந்த முக்கோணம் சமபக்க முக்கோணமாக இருக்கும் என்பதை உறுதிப்படுத்தப் போதுமான முடிவாக இருக்கும்:
- ஒரு முக்கோணத்தின் சுற்றுவட்டமையம், உள்வட்ட ஆரம், நடுக்கோட்டுச்சந்தி, செங்கோட்டுச்சந்தி ஆகியவற்றில் எவையேனும் இரண்டு புள்ளிகள் ஒன்றுபட்டால், அம்முக்கோணம் சமபக்க முக்கோணமாக இருக்கும்.[15]
- ஒரு முக்கோணத்தின் சுற்றுவட்டமையமானது நாகெல் புள்ளியுடன் ஒன்றுபட்டாலும் அல்லது உள்வட்டமையமானது ஒன்பது-புள்ளி வட்டமையத்துடன் ஒன்றுபட்டாலும் அம்முக்கோணம் சமபக்க முக்கோணமாக இருக்கும்.[7]
நடுக்கோடுகளின் பிரிப்பால் உண்டாகும் ஆறு முக்கோணங்கள்
ஒரு முக்கோணத்தின் மூன்று நடுக்கோடுகளும் அம்முக்கோணத்தை ஆறு சிறு முக்கோணங்களாகக் பிரிக்கின்றன.
- இந்த ஆறு சிறு முக்கோணங்களில் எவையேனும் மூன்று முக்கோணங்கள் ஒரேயளவு சுற்றளவு அல்லது ஒரேயளவு உள்வட்ட ஆரம் கொண்டிருந்தால், இருந்தால் மட்டுமே, எடுத்துக்கொள்ளப்பட்ட முக்கோணம் சமபக்க முக்கோணமாக இருக்கும்.[16]:Theorem 1
- இந்த ஆறு சிறு முக்கோணங்களில் எவையேனும் மூன்று முக்கோணங்களின் சுற்றுவட்ட மையங்கள் மூல முக்கோணத்தின் நடுக்கோட்டுச் சந்தியிலிருந்து சம தூரத்தில் ‘இருந்தால், இருந்தால் மட்டுமே’, எடுத்துக்கொள்ளப்பட்ட முக்கோணம் சமபக்க முக்கோணமாக இருக்கும்.[16]:Corollary 7
தளத்திலுள்ள புள்ளிகள்
- P என்பது எடுத்துக்கொள்ளப்பட்ட முக்கோணத்தின் தளத்தில் ஒரு புள்ளி; இப்புள்ளியிலிருந்து முக்கோணத்தின் பக்கங்களின் தூரம் p, q, r ; இப்புள்ளிக்கும் முக்கோணத்தின் மூன்று உச்சிகளுக்கும் இடைப்பட்ட தூரம் x, y, and z எனில், கீழ்க்காணும் முடிவு உண்மையாகும்:[17]:p.178,#235.4
Remove ads
தேற்றங்கள்
மோர்லியின் முச்சமவெட்டித் தேற்றம்:
- ஒரு முக்கோணத்தின் கோண முச்சமவெட்டிகள் சந்திக்கும் புள்ளிகள் ஒரு சமபக்க முக்கோணத்தை அமைக்கின்றன.
ஒரு முக்கோணத்தின் பக்கங்களின் மீது உட்புறமாகவோ அல்லது வெளிப்புறமாகவோ வரையப்படும் சமபக்க முக்கோணங்களின் மையங்கள் ஒரு சமபக்க முக்கோணத்தை அமைக்கின்றன.
சமச்சுற்றளவுச் சமனிலி:
முக்கோணங்களுக்கான சமச்சுற்றளவுச் சமனிலியின்படி, சமச்சுற்றளவு கொண்ட முக்கோணங்களுக்கும் அதிகபட்ச பரப்பளவுள்ள முக்கோணம் சமபக்க முக்கோணமாகும்.[18]
ஒரு சமபக்க முக்கோணத்தின் உட்புறமுள்ள ஒரு புள்ளி P யிலிருந்து அம்முக்கோணத்தின் பக்கங்களின் தூரங்கள் d, e, f எனில்:
- d + e + f = முக்கோணத்தின் செங்குத்துயரம்[19]
இம்முடிவு சமபக்க முக்கோணத்தின் உட்புறத்தேயுள்ள எல்லாப்புள்ளிகளுக்கும் பொருந்தும்.
பாம்ப்யூவின் தேற்றம்: சமபக்க முக்கோணம் ABC இன் தளத்திலமையும் புள்ளி P எனில், PA, PB, PC நீளமுள்ள பக்கங்களைக் கொண்ட ஒரு முக்கோணம் இருக்கும்.
பிற பண்புகள்
ஆய்லரின் சமனின்மையின்படி, சுற்றுவட்ட ஆரத்திற்கும் உள்வட்ட ஆரத்திற்குமான விகிதம் R/r ஆனது எல்லா முக்கோணங்களையும்விட சமபக்க முக்கோணத்தில்தான் மிகச்சிறியதாக இருக்கும். சமபக்க முக்கோணத்தில் R/r = 2 ஆகும்.[20]:p. 198
ஒரு வட்டத்தினுள் வரையப்படும் முக்கோணங்களில் அதிகபட்ச பரப்பளவுள்ள முக்கோணமானது ஒரு சமபக்க முக்கோணம். அதேபோல, ஒரு வட்டத்தைத் தொட்டவாறு வெளிப்புறமாக வரையப்படும் முக்கோணங்களில் குறைந்தபட்ச பரப்பளவுள்ள முக்கோணமானது ஒரு சமபக்க முக்கோணம்.[21]
வேறெந்த அசமபக்க முக்கோணங்களையும் விட, ஒரு சமபக்க முக்கோணத்தின் உள்வட்டத்தின் பரப்புக்கும் அம்முக்கோணத்தின் பரப்புக்கும் உள்ள விகிதம் இன் மதிப்பு மிக அதிகபட்சமானதாக இருக்கும்.[22]
வேறெந்த முக்கோணங்களையும்விட ஒரு சமபக்க முக்கோணத்தில் அதன் பரப்பிற்கும் சுற்றளவின் வர்க்கத்திற்குமுள்ள விகிதம் மிகப் பெரியதாக இருக்கும்.[18]
சமச் சுற்றளவுகளும், A1 , A2 பரப்பளவுகளும் கொண்ட இரு பகுதிகளாக ஒரு சமபக்க முக்கோணம் பிரிக்கப்பட்டால் கீழுள்ள முடிவு உண்மையாகும்[17]:p.151,#J26:
சிக்கலெண் தளத்தில் வரையப்பட்ட ஒரு முக்கோணத்தின் உச்சிகள் z1, z2, z3; மெய்யெண் அல்லாத ஒன்றின் முப்படி மூலம் . கீழுள்ள முடிவு உண்மையாக ‘இருந்தால், இருந்தால் மட்டுமே’ அந்த முக்கோணம் சமபக்க முக்கோணமாக இருக்கும்.[23]:Lemma 2
ஒரு சமபக்க முக்கோணத்தின் உட்புறமுள்ள ஒரு புள்ளி P எனில், இப்புள்ளிக்கும் சமபக்க முக்கோணத்தின் உச்சிகளுக்கும் இடைப்பட்ட தூரங்களின் கூடுதலுக்கும், பக்கங்களிலிருந்து இப்புள்ளியின் தூரங்களின் கூடுதலுக்கும் உள்ள விகிதத்தின் அளவு 2 ஆகும். வேறெந்த முக்கோணத்திலும் விட சமபக்க முக்கோணத்தில் இந்த அளவு மிகக் குறைந்த அளவாகும்.[24]
ABC முக்கோணத்தின் தளத்திலமைந்த ஒரு புள்ளி P. முக்கோணத்தின் உச்சிகள் A B C லிருந்து இப்புள்ளிக்குள்ள தூரங்கள் முறையே p, q, t எனில்,[25]
ஒரு சமபக்க முக்கோணத்தின் உள்வட்டத்தின் மேலமையும் புள்ளி P ; இப்புள்ளிக்கும் சமபக்க முக்கோணத்தின் உச்சிக்கும் இடைப்பட்ட தொலைவுகள் p, q, t எனில்[25]:
சமபக்க முக்கோணம் ABC இன் சுற்றுவட்டத்தின் சிறுவில்லான BC இன் மேலமையும் புள்ளி P ; முக்கோணத்தின் உச்சிகள் A B C லிருந்து இப்புள்ளிக்குள்ள தூரங்கள் முறையே p, q, t எனில்[19]:170[25]:
மேலும் சமபக்க முக்கோணத்தின் BC பக்கத்தின் மீதமையும் புள்ளி D ஆனது, PD = y, DA = z என்றவாறு PA ஐப் பிரிக்குமானால்[19]:172:
- (t ≠ q எனில்)
சமபக்க முக்கோணமாக ’இருந்தால், இருந்தால் மட்டுமே’, சமக்குறிக்கு உண்மையாகும் பல முக்கோணச் சமனிலிகள் உள்ளன.
சமபக்க முக்கோணம், அதிகபட்ச சமச்சீர் கொண்ட முக்கோணமாகும். சமபக்க முக்கோணத்திற்கு அதன் மையத்தைப் பொறுத்து, மூன்று எதிரொளிப்பு அச்சுகளும், மூன்று சுழற்சி அச்சுகளும் உள்ளன. சமபக்க முக்கோணத்தின் சமச்சீர் குலமானது வரிசை ஆறு கொண்ட ஒரு இருமுகக் குலமாகும் (D3).
முக்கோணங்களிலேயே, சமபக்க முக்கோணங்களுக்கு மட்டுமே அதன் ஸ்டெயினர் உள்நீள்வட்டம் ஒரு வட்டமாகும், அதாவது அதன் உள்வட்டமாகும்.

பல வெவ்வேறு வடிவவியல் அமைவுகளில் சமபக்க முக்கோணங்கள் காணப்படுகின்றன. எடுத்துக்காட்டாக ஒரு ஒழுங்கு நான்முகியானது நான்கு சமபக்க முக்கோணங்களால் உருவானதாகும்.
Remove ads
அமைப்பு
கவராயத்தையும் நேர்விளிம்பையும் மட்டும் பயன்படுத்திச் சமபக்க முக்கோணியை வரைய முடியும்.

பரப்பளவு வாய்ப்பாடு காணல்
சமபக்க முக்கோணத்தின் பரப்பளவு காணும் வாய்ப்பாட்டை () பித்தாகரசு தேற்றத்தைப் பயன்படுத்தி அல்லது முக்கோணவியல் மூலம் காணலாம்.
பித்தாகரசு தேற்றம் பயன்படுத்தல்
பொதுவாக ஒரு முக்கோணத்தின் பரப்பளவு காணும் வாய்ப்பாடு:
- , முக்கோணத்தின் அடிப்பக்கம்-a ; உயரம் h .
செங்குத்துயரத்தால் சமபக்க முக்கோணம் இரு சர்வசம செங்கோண முக்கோணங்களாகப் பிரிக்கப்படுகிறது. அவற்றின் ஒரு தாங்கு பக்கத்தின் நீளம் a/2; மற்றொரு தாங்கு பக்கமானது சமபக்க முக்கோணத்தின் செங்குத்துயரம், செம்பக்கத்தின் நீளம் a.
பித்தாகரசின் தேற்றப்படி,
எனவே சமபக்க முக்கோணத்தின் செங்குத்துயரம்:
செங்குத்துயரத்தின் மதிப்பை முக்கோணத்தின் பரப்பளவு காணும் வாய்ப்பாட்டில் பதிலிட சமபக்க முக்கோணத்தின் பரப்பளவு:
முக்கோணவியலைப் பயன்படுத்தல்

முக்கோணத்தின் பரப்பளவு காணும் வாய்ப்பாடு: முக்கோணத்தின் பக்க நீளங்கள் a , b ; அப்பக்கங்களுக்கு இடைப்பட்ட கோணம் C எனில்,
சமபக்க முக்கோணத்தின் ஒரு கோணத்தின் அளவு 60°, பக்க நீளம் a என்பதால் சமபக்க முக்கோணத்தின் பரப்பளவு:
- .
Remove ads
மேற்கோள்கள்
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads