மடக்கை

மடக்கை (Logarithm) என்பது ஏதேனும் ஒரு எண், குறிப்பிட்ட மற்றொரு எண்ணின் (அடிமானம் அல்லது எண்ணடி) எத்தனை அடுக்குகளாக அமையும் (எத்தனை தடவை பெருக்குப்படும்) என்பதை சுருக்கமாக குறிக்கும் ஒரு வகைக் கணிதச் செய்கை ஆகும்.

அடிமானம் 2, அடிமானம் e, அடிமானம் 10 ஆகியவற்றுக்கு வரையப்பட்ட மடக்கை

எடுத்துக்காட்டாக 1000 ஐ 10³ எனச் சுட்டி வடிவில் எழுதலாம்.

1000 = 10³

ஆகவே மட₁₀1000 = 3

அதாவது 10 மூன்று தடவை பெருக்கப்படுவதால் 1000 பெறப்படுகிறது.

இதேபோல்;

32 = 2⁵

ஆகவே மட₂32 = 5

இதன்படி அடி b க்கான மடக்கை X என்பது மட_bX எனக் குறிக்கப்படும்.

மடக்கை அட்டவணை ஜான் நேப்பியர் (கி.பி.1550-1617) என்பவரால் முன்வைக்கப்பட்டது. மடக்கை அட்டவணை கண்டுபிடிக்கப்பட்டதன் மூலம் பெரிய எண்களைக் கொண்டமைந்த கணிதச் செய்கைகள் இலகுவாக்கப்பட்டன. இரு எண்களின் பெருக்கத்தைக் காண்பதற்கு மடக்கை மாற்றம் செய்யப்பட்ட பின் அவற்றை இலகுவாகக் கூட்டமுடியும்:

${\displaystyle \log _{b}(xy)=\log _{b}(x)+\log _{b}(y).\,}$

மடக்கை அட்டவணை அல்லது வழுக்கி மட்டம் ஆகியவற்றைப் பயன்படுத்தி அவற்றின் பெறுமதியை நேரடியாகக் கண்டு பிரதியிடலாம். தற்போதைய மடக்கைகளை குறிப்பிடும் தற்கால முறையினை லியோனார்டு ஆய்லர் வழங்கினர், அவர் 18 ஆம் நூற்றாண்டில் மடக்கைகளை படிக்குறிச் சார்புடன் இணைத்தார்.

அடிமானம் 10 கொண்ட மடக்கை சாதாரண மடக்கை எனவும், அடிமானம் e (≈ 2.718) கொண்ட மடக்கை இயற்கை மடக்கை (Natural Log) எனவும் அழைக்கப்படுகிறது. சாதாரண மடக்கை அறிவியலிலும் பொறியியலிலும் அதிகப்பயன்பாடும், இயற்கை மடக்கை கணிதத்தில், குறிப்பாக நுண்கணிதத்திலும் அதிக பயன்பாடு கொண்டுள்ளன. அடிமானம் 2 கொண்ட மடக்கை கணினி அறிவியலில் அதிகப் பயன்பாடு கொண்டுள்ளது. இதுதவிர மடக்கை அட்டவணைகள் பரந்த கண்ணோடம் கொண்ட அலகுகளை சிறு அளவுகளை அளக்கும் நோக்கத்தைச் சாத்தியமாக்கின. எடுத்துக்காட்டாக டெசிபல் என்பது சைகை ஆற்றல் மடக்கை விகிதம் மற்றும் வீச்சு மடக்கை விகிதத்தை அளவிடும் அலகாகும் (அழுத்தம், ஒலி இரண்டுக்கும்). வேதியலில் pH என்பது திரவ கரைசலின் அமிலத்தன்மையை அளவிடப்பயன்படும் மடக்கை அளவீடாகும்.

மடக்கை கருத்தாக்கத்திற்கான தூண்டுகோல் மற்றும் வரையறை

மடக்கை என்னும் கருத்தாக்கம் அடுக்கேற்றத்தின் தலைகீழ் செயல்பாடு ஆகும். எடுத்துக்காட்டாக, 2 என்ற எண்ணின் மூன்றாவது அடுக்கு (கனம்) 8 ஆகும், ஏனெனில் 8 ஆனது 2 என்ற எண்ணை மூன்று முறை பெருக்குவதால் கிடைக்கிறது.

${\displaystyle 2^{3}=2\times 2\times 2=8.\,}$

எனவே, இதன் மறுதலையாக இரண்டை அடிமானமாகக் கொண்ட 8-இன் மடக்கை 3 ஆகும். அதாவது, log₂ 8 = 3.

அடுக்கேற்றம்

ஒரு எண் b இன் மூன்றாவது அடுக்கானது, அந்த எண்ணின் மூன்று முறை பெருக்கல்பலனுக்குச் சமமாகும். பொதுவாக, b என்பதை அதன் n-வது அடுக்கிற்கு உயர்த்துவது, என்பது b'க்குச் சமமான n காரணிகளைப் பெருக்குவதின் மூலம் பெறப்படுகிறது. இங்கு n என்பது ஒரு இயல் எண் ஆகும். b இன் n-வது அடுக்கு என்பது bn என எழுதப்படுகிறது, அதாவது,

${\displaystyle b^{n}=\underbrace {b\times b\times \cdots \times b} _{n{\text{ factors}}}.}$

அடுக்கேற்றத்தினை b^y வரையிலும் நீட்டிக்க முடியும், இங்கு b என்பது ஒரு நேர்மறை எண் மற்றும் அடுக்கு y என்பது ஏதாவது ஒரு மெய்யெண் ஆகும். எடுத்துக்காட்டாக, b⁻¹ என்பது b இன் நேர்மாறு ஆகும், அதாவது 1/b. (b^{m + n} = b^m · bⁿ உள்ளிட்ட கூடுதல் அடிப்படை விவரங்களுக்கு ^[1] என்பதைப் பார்க்கவும்.)

வரையறை

அடிமானம் b ஐப் பொருத்து ஒரு நேர் மெய்யெண் x இன் மடக்கை, b ஐ x ஐக் கொடுப்பதற்காக உயர்த்தும், 1 க்குச் சமமாக இல்லாத ஒரு நேர்மறை மெய்யெண் அடுக்காகும். வேறு விதமாகக் கூறினால், அடிமானம் b க்கு x இன் மடக்கை என்பது சமன்பாட்டிற்கான தீர்வான y ஆகும்.^[2]

${\displaystyle b^{y}=x.\,}$

மடக்கையானது "log_b(x)" எனக் குறிக்கப்படிகிறது (இதனை "மடக்கை x அடிமானம் b" அல்லது "அடிமானம்-b xஇன் மடக்கை" என உச்சரிக்க வேண்டும்).

எடுத்துக்காட்டுகள்

எடுத்துக்காட்டாக, log₂(16) = 4, ஏனெனில் 2⁴ = 2 ×2 × 2 × 2 = 16. மடக்கைகள் எதிர்மறையாகவும் இருக்கலாம்:

${\displaystyle \log _{2}\!\left({\frac {1}{2}}\right)=-1,\,}$

ஏனெனில்

${\displaystyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$

மூன்றாவது எடுத்துக்காட்டு: log₁₀(150) இன் மதிப்பு தோராயமாக 2.176, அது 150 10² = 100 மற்றும் 10³ = 1000 இடையே அமைந்துள்ளதைப்போல் 2க்கும் 3க்கும் இடையில் அமைந்துள்ளது. இறுதியாக, எந்த அடிமானம் bக்கும், log_b(b) = 1 மற்றும் log_b(1) = 0, ஏனெனில் முறையே b¹ = b மற்றும் b⁰ = 1 ஆகும்.

மடக்கை அட்டவணையைப் பயன்படுத்துதல்

மடக்கை அட்டவணையின் ஒரு பகுதிமாதிரி

மடக்கை அட்டவணையில் நிரலில் 1.0,1.1,1.2... எனக் குறிக்கப்பட்டுள்ள எண்கள் மடக்கை காணப்பட வேண்டிய எண்ணின் முதலிரு இலக்கங்களைக் குறிக்கும். மற்றைய இலக்கங்கள் நிரையில் காட்டப்பட்டவற்றால் கொள்ளப்படும். முதலில் எண் முதலாம் தசம நிலை கொண்ட நியம நிலைக்கு மாற்றப்படுதல் வேண்டும்.

எ.கா:

1.5 க்கு மடக்கைப் பெறுமதி காண்பதாயின் ; உண்மையில் மடக்கைப் பெறுமதி என்பது 1.5 =10^x எனக்கொண்டால் x இன் பெறுமதியே அட்டவணையில் தரப்படும்.

${\displaystyle \log(1.5)=0.1761}$ (சிவப்பால் வட்டமிடப்பட்டது)

15 க்கான மடக்கை; இதனை 1.5 X 10 ¹ என் நியம நிலையில் எழுதலாம். ஆகவே

${\displaystyle \log(15)=1.1761}$

1.04 க்கான மடக்கை

${\displaystyle \log(1.04)=0.0170}$ (நீலத்தால் வட்டமிடப்பட்டது)

மடக்கையைப் பயன்படுத்திப் பெருக்கல்

பெருக்குதல் செயற்பாடு ஒன்றைச் செய்வதற்கு அவற்றின் மடக்கைப் பெறுமதியைக் கண்டு அவற்றைக் கூட்டிப் பெற்ற தொகைக்கு முரண் மடக்கை காண்பதன் மூலம் அடையலாம். இது பெரிய சிக்கலான எண்களைப் பெருக்குவதை இலகுவாக்கும்.

எ.கா: 1.5 x 1.04 எனும் பெருக்கலைச் செய்வதாயின்,இதை மடக்கையாக மாற்றவேண்டும்.

${\displaystyle \log(1.5*1.04)=\log(1.5)+\log(1.04).\,}$

= 0.1761 + 0.0170

= 0.1931

இனி 0.1931க்கு எதிர் மடக்கை(Anti Log) அதாவது அட்டவணையில் உட்பெறுமதியாக இருக்கும் இடத்தின் நிலைகளைக் கண்டறிதல் வேண்டும். இது 1.56 ஆகும். (பச்சையால் குறிக்கப்பட்டது).

எனவே: 1.5 x 1.04 = 1.56

மடக்கை முற்றொருமைகள்

மடக்கையைத் தொடர்புபடுத்தி அமைக்கப்படும் பல்வேறு வாய்ப்பாடுகள் காணப்படுகின்றன. இவை மடக்கை முற்றொருமைகள் எனப்படும்.^[3]

பெருக்கல் முற்றொருமை

இரு எண்களின் பெருக்கத்துக்கான மடக்கை அவ்வெண்களின் தனித்தனி மடக்கைப் பெறுமானங்களின் கூட்டுத்தொகைக்குச் சமனாகும்:

${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y.\,}$

வகுத்தல் முற்றொருமை

இரு எண்களின் விகிதங்களுக்கான (வகுத்தலுக்கான) மடக்கை அவ்வெண்களின் தனித்தனி மடக்கைப் பெறுமானங்களின் வித்தியாசத்திற்குச் சமனாகும்:

${\displaystyle \log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}x-\log _{b}y.\,}$

அடுக்கு காணல் முற்றொருமை

ஒரு எண்ணின் p அடுக்கின் மடக்கைப் பெறுமதி அவ்வெண்ணின் மடக்கைப் பெறுமதியை p தடவைகள் பெருக்குவதற்குச் சமன்:

${\displaystyle \log _{b}(x^{p})=p\log _{b}x.\,}$

அடுக்கு காணல் முற்றொருமை

ஒரு எண்ணின் p மூலத்தின் மடக்கைப் பெறுமதி அவ்வெண்ணின் மடக்கைப் பெறுமதியை p யினால் வகுப்பதற்குச் சமன் :

${\displaystyle \log _{b}({\sqrt[{p}]{x}}\,)={\frac {\log _{b}x}{p}}.\,}$

எடுத்துக்காட்டுகள்:

${\displaystyle \log _{3}243=\log _{3}(9\times 27)=\log _{3}9+\log _{3}27=2+3=5\,}$

${\displaystyle \log _{2}16=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}64-\log _{2}4=6-2=4}$

${\displaystyle \log _{2}64=\log _{2}(2^{6})=6\log _{2}2=6\,}$

${\displaystyle \log _{10}\!\left(\!{\sqrt {1000}}\,\right)={\frac {1}{2}}\log _{10}(1000)={\frac {3}{2}}=1.5}$

அடிமானங்களை மாற்றுதல்

log_b(x) எனும் x , b உடன் தொடர்புடைய மடக்கையை எழுமாற்றான அடிமானமான k க்கு மாற்றுவதாயின்:

${\displaystyle \log _{b}{x}={\frac {\log _{k}{x}}{\log _{k}{b}}}.\,}$

இவ்வாறே கணிப்பான்களில் அடிமானம் 10, கணித மாறிலி e என்பவற்றுக்கு மாற்றப்படுகிறது.:

${\displaystyle \log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.\,}$

அதாவது தரப்பட்ட எண் x மற்றும் அதன் மடக்கை log_b(x) தெரிந்த அடிமானம் b க்கு பின்வருமாறு தரப்படும்:

${\displaystyle b=x^{\frac {1}{\log _{b}(x)}}.}$

குறிப்பிட்ட அடிமானங்கள்

2 ஐ அடிமானமாகக் கொண்ட மடக்கை வரைபடம் x அச்சை (கிடை அச்சு) 1ல் கடந்து ஆய ஆச்சுகள் (2, 1), (4, 2), மற்றும் (8, 3) வழியே செல்கிறது. எடுத்துக்காட்டாக, log₂(8) = 3, ஏனெனில் 2³ = 8. வரைபடம் y அச்சுக்கு அருகில் செல்கிறது, ஆனால் அதை வெட்டுவதில்லை.

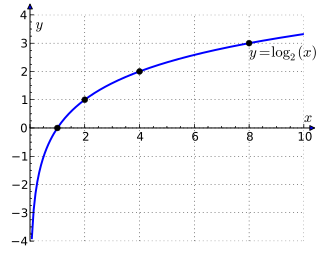
அடிமானங்களில் b = 10, b = e ( ≈ 2.71828), b = 2 மூன்றும் குறிப்பிடத் தக்கவை. கணிதத்தில் அடிமானம் e அதிகம் பயன்பாடு கொண்டுள்ளது. அடிமானம் 10, தசம எண்மான முறையில் கணக்கீடுகளை எளிதாகச் செய்யப் பயன்படுகிறது^[4]

${\displaystyle \log _{10}(10x)=\log _{10}(10)+\log _{10}(x)=1+\log _{10}(x).\ }$

இவ்வாறு, log₁₀(x) என்பது ஒரு நேர் முழு எண் x கொண்டிருக்கும் தசம இலக்கங்களைக் குறிக்கிறது: இலக்கங்களின் எண்ணிக்கையானது log₁₀(x) என்பதை விட கண்டிப்பாக அதிகமாக இருக்கும் மிகச் சிறிய முழு எண் ஆகும்.^[5] எடுத்துக்காட்டாக, log₁₀(1430) இன் மதிப்பு தோராயமாக 3.15. அடுத்த முழு எண் 4, இது 1430 இல் உள்ள இலக்கங்களின் எண்ணிக்கை ஆகும். இயற்கை மடக்கை மற்றும் ஈரடிமான மடக்கை இரண்டும் தகவல் கோட்பாட்டில் பயன்படுத்தப்படுகின்றன, அவற்றின் பயன்பாட்டைப் பொருத்து தகவலின் அடிப்படை அலகான முறையே நேட் மற்றும் பிட் போன்றவை பயன்படுத்தப்படுகின்றன.^[6] ஈரடிமான மடக்கையானது, ஈரடிமான எண்முறை பரவலாகப் பயன்படுத்தப்படும் கணினி அறிவியல் மற்றும் ஒளிப்படவியலில் வெளிப்பாட்டு மதிப்பினை அளக்கவும் பயன்படுகிறது.^[7]

கீழ்க்காணும் அட்டவணை இந்த அடிமானங்களில் அமைந்த மடக்கைகளின் பொதுவான குறியீடுகளையும் அவை பயன்படும் துறைகளையும் தருகிறது. பல துறைகளில் log_b(x) க்குப் பதில் log(x) என எழுதப்படுகிறது. அடிமானங்கள் அந்தந்த சூழ்நிலைக்கேற்பத் தீர்மானித்துக் கொள்ளப்படுகிறது. சில இடங்களில் குறியீடு, ^blog(x) -ம் பயன்படுத்தப்படுகிறது.^[8] ஐஎஸ்ஓ குறியீடு நிரல் சீர்தரத்துக்கான அனைத்துலக நிறுவனம் தரும் குறியீடுகளைத் தருகிறது.^[9] log x என்று குறிப்பிடும் முறை எல்லா மூன்று அடிமான முறைகளிலும் பயன்படுத்தப்படும் காரணத்தால் (அல்லது அடிமானத்தை தீர்மானிக்க முடியாத போது அல்லது அடிமான மதிப்பு கொடுக்கப்படாத போது), அடிமானமானது துறை அல்லது சூழலின் அடிப்படையில் உய்த்துணரப்படுகிறது. கணினி அறிவியலில் மடக்கை என்பது பொதுவாக, முறையே log₂ மற்றும் log_e என்பவற்றைக் குறிக்கிறது..^[10] பிற சூழல்களில் பொதுவாக மடக்கை அல்லது log என்பது log₁₀ என்பதைக் குறிக்கிறது.^[11]

அடிமானம் b	logb(x) இன் பெயர்	ISO குறியீடு	ஏனைய குறியீடுகள்	பயன்பாடு
2	ஈரடிமான மடக்கை	lb(x)[12]	ld(x), log(x), lg(x)	கணனி அறிவியல், தகவற் கோட்பாடு, கணிதம்
e	இயற்கை மடக்கை	ln(x)[nb 1]	log(x) (கணிதம், பல நிரல் மொழிகள் [nb 2])	கணித பகுவியல், இயற்பியல், வேதியியல், புள்ளியியல், பொருளியல் மற்றும் சில பொறியியல் துறைகள்
10	சாதாரண மடக்கை	lg(x)	log(x) (பொறியியல், உயிரியல், வானியல்),	பல்வேறு பொறியியல் துறைகள், மடக்கை அட்டவணைகள் tables, கணிப்பான்கள்