E (лік)
From Wikipedia, the free encyclopedia
Remove ads
Лік e (таксама лік Эйлера або пастаянная Непера) — важная матэматычная пастаянная, якая акрамя іншага з'яўляецца асновай натуральнага лагарыфма. Звычайна ў курсах матэматычнага аналізу пастаянную азначаюць як граніцу паслядоўнасці

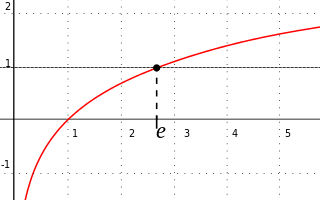
Сіняя крывая: ex;
пункцірная крывая: 2x;
штрыхавая крывая: 4x.
На рысунку відаць, што чырвоная прамая, праведзеная праз пункт (0,1) з нахілам 1, не з'яўляецца датычнай да графікаў апошніх дзвюх функцый.
пры імкненні n да бесканечнасці. Такі выраз ўзнікае пры вывучэнні складанага працэнта.
Эйлераў лік можна вылічыць і як суму бесканечнага рада[1]
Пастаянную можна вызначыць мноствам спосабаў. Напрыклад, іншы раз за азначэнне бяруць наступны факт: e — адзіны рэчаісны лік, такі што вытворная (нахіл датычнай прамой) функцыі f(x) = ex у пункце x = 0 роўная 1.[2] Функцыя ex, вызначаная такім чынам, называецца экспаненцыяльнай функцыяй (або натуральнай паказчыкавай функцыяй), адваротнай да яе функцыяй з'яўляецца лагарыфм па аснове e — т.зв. натуральны лагарыфм. Натуральны лагарыфм дадатнага ліку k можна таксама вызначыць напрамую, як плошчу пад крывой y = 1/x, якая заключана паміж значэннямі аргумента x = 1 і x = k. Лік e — такі лік, натуральны лагарыфм якога роўны 1. Ёсць і іншыя іншыя азначэнні.
Пастаянную e часам называюць Эйлеравым лікам у гонар швейцарскага матэматыка Леанарда Эйлера (не блытаць з γ — пастаяннай Эйлера-Маскероні, якую іншы раз называюць проста пастаяннай Эйлера). Лік e таксама вядомы як пастаянная Непера, бо першыя вядомыя ўпамінанні гэтага ліку былі знойдзены ў працах Джона Непера, які выкарыстоўваў гэты лік у якасці асновы лагарыфма[3]. Абазначаць лік літарай e пачаў Эйлер.[4] Лік e мае вялікае значэнне ў матэматыцы[5] і па важнасці стаіць побач с такімі лікамі як 0, 1, π і ўяўная адзінка i. Усе пяць лікаў сустракаюцца, мабыць, ва ўсіх галінах матэматыкі. Цікава, што ўсе яны ўваходзяць у тоеснасць Эйлера:
Як і пастаянная π, e — ірацыянальны лік: г.зн. яго нельга запісаць у выглядзе дзелі двух цэлых лікаў. Больш таго, ён трансцэндэнтны: г.зн. не існуе ненулявога мнагачлена з рацыянальнымі каэфіцыентамі, для якога лік e быў бы коранем.
Лікавае значэнне e з дакладнасцю 50 дзесятковых знакаў пасля коскі:
- 2.71828182845904523536028747135266249775724709369995... (паслядоўнасць A001113 у OEIS).
Remove ads
Гісторыя
Першыя ўскосныя ўпамінанні Эйлерава ліку сустракаюцца ў табліцах ў дадатку Неперавай працы па лагарыфмах, апублікаванай у 1618 годзе[6]. Праца ўтрымлівала не саму пастаянную, а проста спіс лагарыфмаў, вылічаных па аснове, прыблізна роўнай 1/e. Мяркуюць, што табліцу напісаў Уільям Оўтрэд. Адкрыццё самой пастаяннай прыпісваецца Якабу Бернуллі, які спрабаваў знайсці значэнне граніцы (якая раўняецца e):
Першыя вядомыя прамыя ўпамінанні пастаяннай Непера былі знойдзены ў пісьмах Лейбніца да Гюйгенса ў 1690 і 1691 гг. Там Лейбніц карыстаецца пастаяннай і абазначае яе літарай b. Леанард Эйлер ужыў літару e для абазначэння асновы натуральных лагарыфмаў у пісьме да Хрысціяна Гольдбаха 25 лістапада 1731 года.[7] Эйлер пачаў абазначаць пастаянную літарай e недзе ў 1727 ці 1728 годзе, у неапублікаванай працы па выбуховых сілах у гарматах,[8], а першым з'яўленнем e ў публікацыі была Эйлерава Mechanica (1736). І хоць у наступныя гады некаторыя даследчыкі абазначалі лік літарай c, абазначэнне e было больш распаўсюджаным і ў выніку стала агульнапрынятым.
Remove ads
Прымяненні
Складаны працэнт

Якаб Бернулі адкрыў пастаянную, рашаючы задачу аб складаным працэнце:[6]
- Пачатковая сума на рахунку $1.00, працэнтная стаўка па ўкладу складае 100% гадавых. Калі працэнты налічваюцца адзін раз у канцы года, сума на рахунку ў канцы года стане $2.00. Што адбудзецца, калі на працягу года працэнты налічваюцца на рахунак больш часта? (Пры гэтым налічаны на рахунак даход таксама пускаецца ў абарот пад тыя ж працэнты).
Калі працэнты пераводзяцца на рахунак двойчы ў год, сума будзе прырастаць на 50% кожныя 6 месяцаў, і такім чынам пачатковы $1 дамнажаецца на 1.5 двойчы, даючы $1.00×1.52 = $2.25 у канцы года. Паквартальнае накапленне дае $1.00×1.254 = $2.4414..., а штомесячнае накапленне дае $1.00×(1+1/12)12 = $2.613035... Калі ёсць n прамежкаў накаплення, працэнт на кожным прамежку будзе 100%/n і сума ў канцы года складзе $1.00×(1 + 1/n)n.
Бернулі заўважыў, што гэта паслядоўнасць прыбліжаецца да граніцы з ростам n і, адпаведна, са здрабненнем прамежкаў налічэння. Штотыднёвае налічэнне (n = 52) дае $2.692597..., тады як штодзённае налічэнне (n = 365) дае $2.714567..., толькі на два цэнты больш. Граніца пры неабмежаваным нарастанні n і ёсць лік, вядомы цяпер як e; пры непарыўным налічэнні, сума на рахунку дасягне $2.7182818.... У агульным выпадку, пачатковая сума на рахунку $1 і гадавы прырост даходу R долей пасля t гадоў дадуць у выніку eRt долараў пры непарыўным налічэнні. (Тут R — доля, а не працэнт. Так што, для 5% гадавых, R = 5/100 = 0.05.)
Выпрабаванні Бернуллі
Лік e ўзнікае і ў тэорыі імавернасцей. Няхай гулец робіць стаўкі ў гульнявым аўтамаце. Імавернасць выйгрышу пры адном запуску аўтамата роўная 1 на n. Ігрок робіць стаўку n разоў. Тады для вялікіх n (напрыклад, мільёна) імавернасць, што гуляка прайграе ўсе стаўкі прыблізна раўняецца 1/e. Так, для n = 20 гэта ўжэ 1/2.72.
Гэта прыклад выпрабаванняў Бернуллі. Кожны раз, калі ігрок кідае манетку ў аўтамат (робіць стаўку), шанц выйграць — адзін на мільён. Запуск аўтамата мільён разоў мадэліруецца біномным размеркаваннем, якое цесна звязана з біномам Ньютана. Імавернасць k разоў выйграць пры мільёне спроб роўная:
У прыватнасці, імавернасць ні разу не выйграць (k = 0) роўная:
Гэта значэнне вельмі блізкае да наступнай граніцы:
Беспарадкі
Пастаянная e ўзнікае і ў камбінаторыцы. Прыкладам можа служыць т.зв. задача аб беспарадках, таксама вядомая як задача разбору шапак[9], якою займаліся Якаб Бернуллі і П'ер Раймонд дэ Мантмор (фр.: Pierre Rémond de Montmort). Вось як гучыць гэта задача:
- На вечарынку запрошана n гасцей. У дзвярах кожны госць аддае сваю шапку дварэцкаму, які затым ложыць яе ў адну з n скрынь, кожная з якіх пазначана іменем аднаго з гасцей. Але дварэцкі не знае гасцей па імёнах (а мо проста чытаць не ўмее) і таму кідае шапкі ў скрыні як папала. Задача дэ Мантмора — знайсці імавернасць таго, што ні адна шапка не трапіла ў патрэбную скрыню. Адказ такі:
Калі лік гасцей n імкнецца да бесканечнасці, pn прыбліжаецца к 1/e. Больш таго, колькасць спосабаў раскідаць шапкі па каробках так, каб ні адна не папала куды трэба, для любога n раўняецца ліку n!/e, акругленаму да найбліжэйшага цэлага.[10]
Асімптотыкі
Лік e натуральным чынам узнікае ў сувязі з мноствам задач, якія закранаюць асімтотыку. Выдатным прыкладам з'яўляецца формула Сцірлінга для асімптотыкі фактарыяла, куды ўваходзяць і e, і π:
Адсюль можна атрымаць:
Remove ads
Лік e ў аналізе
Важнасць ліку e ў аналізе тлумачыцца найперш патрэбай ажыццяўляць дыферэнцаванне і інтэграванне паказчыкавых функцый і лагарыфмаў.[11] Паказчыкавая функцыя агульнага выгляду y = ax мае вытворную, якая задаецца як граніца:
Самая правая граніца ў выразе не залежыць ад зменнай x: яна залежыць толькі ад асновы a. Калі аснова роўная e, граніца раўняецца адзінцы, і такім чынам e вызначаецца з ураўнення:
Адсюль відаць, што паказчыкавая функцыя з асновай e асабліва зручная пры ажыццяўленні розных аперацый у аналізе. Выбар ліку e ў якасці асновы паказчыкавай функцыі значна спрашчае разлікі, у якіх неабходна знаходзіць вытворную.
Выкарыстанне ліку e ў якасці асновы таксама спрашчае інтэграванне і дыферэнцаванне лагарыфмічных функцый.[12] Вылічым вытворную функцыі loga x па азначэнню, г.зн. як граніцу:
дзе на апошнім кроку зроблена падстаноўка u = h/x. Апошняя граніца ў гэтым ланцужку роўнасцей ізноў залежыць толькі ад асновы a, і калі аснова — e, граніца раўняецца адзінцы. Такім чынам,
У гэтым выпадку лагарыфм называецца натуральным і абазначаецца як ln. Ён зручнейшы за лагарыфмы па іншых асновах, бо пры аперацыях дыферэнцавання і інтэгравання не прыходзіцца ўсюды цягаць нязручныя множнікі выгляду ln a.
Такім чынам, лік a = e з дапамогай паняцця вытворнай можна вызначыць двума спосабамі. Першы з іх — прыняць, што вытворная паказчыкавай функцыі ax роўная ax, і адсюль знайсці a. Другі — сказаць, што вытворная лагарыфма з асновай a раўняецца 1/x і адтуль знайсці a. Абодва спосабы раўназначныя і даюць аднолькавы вынік.
Іншыя азначэнні

Лік e можна вызначыць і іначай: як граніцу паслядоўнасці, ці як суму бесканечнага рада, ці праз нейкія інтэгралы. Вышэй было прыведзена толькі два раўназначныя азначэнні (уласцівасці) ліку e, а іменна:
1. Лік e — гэта адзіны дадатны рэчаісны лік, такі што
2. Лік e — гэта адзіны дадатны рэчаісны лік, такі што
Можна паказаць, што наступныя тры азначэнні раўназначныя дадзеным раней:
3. Лік e — гэта граніца паслядоўнасці:
Ці граніца функцыі:
4. Лік e — гэта сума бесканечнага рада
дзе n! — фактарыял ліку n.
5. Лік e — адзіны дадатны рэчаісны лік, такі што
Remove ads
Уласцівасці
Аналіз
Паказчыкавая функцыя ex мае важнае значэнне яшчэ і таму, што гэта адзіная не роўная тоесна нулю функцыя (з дакладнасцю да пастаяннага множніка), якая супадае са сваёй вытворнай
і такім чынам, яе першаісная таксама роўная:
Ступенна-паказчыкавыя функцыі

Глабальны максімум функцыі
дасягаецца ў x = e. Гэтак жа, x = 1/e — пункт, дзе дасягаецца глабальны мінімум функцыі
вызначанай для дадатных x.
Больш агульна, x = e−1/n будзе пунктам глабальнага мінімума функцыі
для любога n > 0.
Па тэарэме Леанарда Эйлера, бесканечная ступенная вежа
- або ∞
збягаецца, калі і толькі калі e−e ≤ x ≤ e1/e (або прыблізна паміж 0.0660 і 1.4447).
Тэорыя лікаў
Лік e ірацыянальны. Эйлер даказаў гэта, паказаўшы, што яго раскладанне ў просты непарыўны дроб бесканечнае.[13] (Гл. таксама доказ ірацыянальнасці ліку e, які даў Жан Фур'е.)
Больш таго, па тэарэме Ліндэмана — Веерштраса e — трансцэндэнтны лік, г.зн. ён не з'яўляецца коранем ніякага ненулявога мнагачлена з рацыянальнымі каэфіцыентамі. Гэта быў першы лік, чыя трансцэндэнтнасць была даказана, і які пры гэтым не быў адмыслова пабудаваны для гэтае мэты (як напрыклад лікі Ліувіля). Трансцэндэнтнасць ліку e даказаў Шарль Эрміт у 1873 годзе.
Была выказана здагадка, што лік e нармальны, г.зн. калі запісаць лік e ў сістэме злічэння для адвольнай асновы, магчымыя лічбы будуць раўнамерна размеркаваны (сустракаюцца з аднолькавай імавернасцю ў любой паслядоўнасці дадзенай даўжыні).
Камплексныя лікі
Паказчыкавую функцыю ex можна запісаць у выглядзе рада Тэйлара:
Гэты рад дазваляе выявіць мноства важных уласцівасцей функцыі ex, нават калі x прымае камплексныя значэнні, яго звычайна выкарыстоўваюць, каб пашырыць азначэнне ex на ўсе камплексныя лікі. Рад для паказчыкавай функцыі разам з радамі Тэйлара для сінуса і косінуса, дазваляе вывесці формулу Эйлера:
справядлівую для ўсіх x. Асобны выпадак пры x = π — тоеснасць Эйлера:
з якой вынікае, што на галоўнай галіне лагарыфма,
Больш таго, карыстаючыся правіламі ступенявання, атрымліваем тоеснасць
якая называецца формулай Муаўра.
Дыферэнцыяльныя ўраўненні
Функцыя агульнага выгляду
ёсць рашэнне дыферэнцыяльнага ўраўнення:
Remove ads
Прадстаўленні
Лік e можна задаць рознымі спосабамі: як бесканечны рад, бесканечны здабытак, непарыўны дроб, ці граніцу паслядоўнасці. Як правіла, асабліва ў курсах матэматычнага аналізу, пастаянную азначаюць як граніцу
ці як суму рада
якая атрымліваецца з вышэйзгаданага ступеннага рада для ex у x = 1.
Менш вядома прадстаўленне ліку e непарыўным дробам (паслядоўнасць A003417 у OEIS), якое атрымаў Леанард Эйлер:
што ў звычайным запісе выглядае як:
А гэты ланцуговы дроб e збягаецца ў тры разы хутчэй:
або ў разгорнутым запісе:
Вядома таксама многа іншых прадстаўленняў ліку e ў выглядзе непарыўных дробаў, радоў, граніц паслядоўнасцей, бесканечных здабыткаў.
Стахастычныя прадстаўленні
Акрамя дакладных аналітычных выразаў для ліку e, ёсць і імавернасныя метады ацэнкі ліку e. Вось адзін з іх: няхай ёсць бесканечная паслядоўнасць незалежных выпадковых велічынь X1, X2..., кожная з якіх раўнамерна размеркавана на адрэзку [0, 1]. Няхай V — найменшы лік n, для якога сума першых n членаў паслядоўнасці большая за 1:
Тады матэматычнае спадзяванне велічыні V раўняецца e:[15][16]
Колькасць вядомых дзесятковых разрадаў
За апошнія дзесяцігоддзі колькасць вядомых лічбаў ліку e рэзка ўзрасла. Гэта стала магчыма як дзякуючы росту вылічальных магутнасцей, так і дзякуючы ўдасканаленню алгарытмаў.[17][18]
Remove ads
У камп'ютарнай культуры
У сучаснай інтэрнэт-культуры як асобы, так і арганізацыі часта аддаюць даніну павагі ліку e.
У IPO кампаніі Google у 2004 годзе было аб'яўлена, што кампанія мае намер павялічыць свой прыбытак на $2,718,281,828, што ўяўляе сабой першыя 10 лічбаў ліку e. Google таксама прафінансавала рэкламныя шчыты[28], якія з'явіліся ў цэнтры Крэмніевай даліны, а пазней у Кембрыджы (штат Масачусетс); Сіэтле (штат Вашынгтон) і Осціне (штат Тэхас). На шчытах было напісана
- {first 10-digit prime found in consecutive digits of e}.com
Па-беларуску гэта гучала б як:
- {першы 10-разрадны просты лік, знойдзены ў паслядоўных лічбах ліку e}.com
Рашэнне гэтай задачы і наведванне рэкламуемага сайта (цяпер не існуе) вяло да яшчэ больш складанай задачы, рашыўшы якую можна было трапіць на сайт Google Labs, дзе наведвальніку прапаноўвалася пакінуць сваё рэзюме.[29] Першы 10-разрадны просты лік у дзесятковым запісе e — 7427466391, і пачынаецца ён на 99-й лічбе.[30]
Яшчэ цікавы прыклад, Дональд Кнут прысвойвае сваёй праграме Metafont нумары версій, якія прыбліжаюцца к ліку e. Паслядоўныя версіі пры гэтым выглядаюць так: 2, 2.7, 2.71, 2.718 і гэтак далей. Падобным жа чынам назначаюцца і нумары версій яго TeXа, якія пачынаючы з версіі 3.0 прыбліжаюцца к ліку π[31]: 3.0, 3.1, 3.14, 3.141 і г.д.
Remove ads
Зноскі
Літаратура
Спасылкі
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads










![{\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ce0cd8eb0003d22f6e68f69c95cf434c43bebc58)











![{\displaystyle {\begin{aligned}e^{x}&=\int _{-\infty }^{x}e^{t}\,dt\\[8pt]&=\int _{-\infty }^{0}e^{t}\,dt+\int _{0}^{x}e^{t}\,dt\\[8pt]&=1+\int _{0}^{x}e^{t}\,dt.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/946f1ea90686802e25ec4cfee5032a5063f61b02)
![{\displaystyle {\sqrt[{x}]{x}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)
![{\displaystyle f(x)={\sqrt[{x}]{x}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e15600c8e263f973cca6db5347531ea5a6846aa8)













![{\displaystyle e=[2;1,\mathbf {2} ,1,1,\mathbf {4} ,1,1,\mathbf {6} ,1,1,...,\mathbf {2n} ,1,1,...]=[1;\mathbf {0} ,1,1,\mathbf {2} ,1,1,\mathbf {4} ,1,1,...,\mathbf {2n} ,1,1,...],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/aa0962ab213c4d99f0c263ec1a753f75f1230ec8)

![{\displaystyle e=[1;0.5,12,5,28,9,44,13,\ldots ,4(4n-1),(4n+1),\ldots ],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b4cb71149be6d3d2beb14c6785740cc1c6c46580)


![{\displaystyle \mathbb {E} [V]=e.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/116f71eed6777b17edf73c95103ba51d65215687)