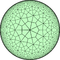
Треугольная мозаика порядка 7

Треугольная мозаика порядка 7 — это правильная мозаика на гиперболической плоскости с символом Шлефли {3,7}.

Соты {3,3,7}^[англ.] ииеют в качестве вершинной фигуры мозаику {3,7}.

Треугольная мозаика порядка 7
Тип	Однородная гиперболическая мозаика
Конфигурация вершины	37
Символ Шлефли	{3,7}
Символ Витхоффа	7 | 3 2
Симметрии	[7,3], (*732)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	Семиугольная мозаика
Свойства	изогональная, хиральная

Поверхность Гурвица

Подробное рассмотрение темы: Поверхность Гурвица

Группа симметрии мозаики — группа треугольника (2,3,7), а фундаментальной областью действий группы является треугольник Шварца (2,3,7). Это наименьший гиперболический треугольник Шварца, а потому, по теореме Гурвица об автоморфизмах, мозаика является универсальной, покрывая все поверхности Гурвица (римановы поверхности с максимальной группой симметрии), задавая им триангуляризацию, группа симметрии которой равна группе автоморфизмов римановой поверхности.

Наименьшая из них — квартика Клейна^?!, поверхность рода 3 с наибольшей симметрией, вместе с мозаикой из 56 треугольников, сходящихся в 24 вершинах. Квартика имеет в качестве группы симметрии простую группу порядка 168, известную как PSL(2,7). Результирующая поверхность может, в свою очередь, быть погружена в евклидово трёхмерное пространство, давая малый кубокубооктаэдр^{[англ.][1]}.

Двойственная мозаика для семиугольной мозаики порядка 3 имеет ту же группу симметрии, а потому даёт семиугольные мозаики поверхностей Гурвица.

Группа симметрии треугольной мозаики порядка 7 имеет в качестве фундаментальной области треугольник Шварца (2,3,7), которая приводит к этой мозаике.

Малый кубокубооктаэдр[англ.] является многогранным вложением квартики Клейна?![1], которая, подобно всем поверхностям Гурвица, является фактор-мозаикой.

Связанные многогранники и мозаики

Мозаика связана с двумя звёздными мозаиками, имея то же расположение вершин^[англ.]: Гептаграммная мозаика порядка 7^[англ.], {7/2,7} и Семиугольная мозаика с гептпаграмным порядком^[англ.], {7,7/2}.

Эта мозаика является топологически частью последовательности правильных многогранников с символом Шлефли {3,p}.

*n32 симметрии правильных мозаик: 3ⁿ or {3,n}

Сферическая				Евклидова	Компактная гипербол.		Пара- компактная	Некомпактная гиперболическая
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

Эта мозаика является частью ряда правильных мозаик {n,7}:

Мозаики вида {n,7}
Сферические	Гиперболические мозаики
{2,7}	{3,7}	{4,7}	{5,7}	{6,7}	{7,7}	{8,7}	...	{∞,7}

По построению Витхоффа существует восемь гиперболических однородных мозаик, которые могут основываться на правильной семиугольной мозаике.

Если рисовать плитки раскрашенными в красный цвет на месте исходных восьмиугольников, в жёлтый цвет на месте исходных вершин и в синий цвет на месте исходных рёбер, имеется 8 форм.

Однородные семиугольные/треугольные мозаики[англ.]
Симметрия: [7,3], (*732)[англ.]							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	2t{7,3}[англ.]=t{3,7}	2r{7,3}	rr{7,3}[англ.]	tr{7,3}	sr{7,3}
Однородные двойственные мозаики
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14[англ.]	V3.3.3.3.7

Смотрите также

• Тетраэдральные соты порядка 7^[англ.]
• Список правильных многомерных многогранников и соединений
• Список однородных мозаик на евклидовой плоскости
• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Треугольная мозаика
• Однородные мозаики на гиперболической плоскости