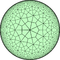
Усечённая треугольно-семиугольная мозаика

Усечённая треугольно-семиугольная мозаика — это полуправильное замощение гиперболической плоскости. В каждой вершине имеется один квадрат, один шестиугольник и один четырнадцатиугольник . Символ Шлефли мозаики — tr{7,3}.

Усечённая треугольно-семиугольная мозаика
Тип	Однородная гиперболическая мозаика
Конфигурация вершины	4.6.14
Символ Шлефли	tr{7,3} или ${\displaystyle t{\begin{Bmatrix}7\\3\end{Bmatrix}}}$
Символ Витхоффа	2 7 3 |
Симметрии	[7,3], (*732)
Диаграммы Коксетера — Дынкина	или
Двойственная мозаика	разделенная ромбическая мозаика порядка 3-7[англ.]
Свойства	изогональная

Однородные раскраски

Есть только одна однородная раскраска усечённой треугольно-семииугольной мозаики. (Цвета в вершине по индексам: 123.)

Симметрия

Каждый треугольник в двойственной разделенной ромбической мозаике порядка 3-7^[англ.] представляет фундаментальную область построения Витхоффа для группы симметрии [7,3].

Двойственная мозаика называется разделённой семиугольной мозаикой порядка 3, состоящей из полного разбиения семиугольной мозаики, показанной здесь с чередующимися цветами.

Связанные многогранники и замощения

Это замощение можно считать членом последоавательности однородных объектов с вершинной фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются всеусечёнными^[англ.] многогранники (зоноэдры), показанные ниже как сферические мозаики. Для p > 6 членам последоавательности являются замощения гиперболической плоскости, начиная с усечённой треугольно-семиугольной мозаики.

*n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n

Симметрия *n32[англ.] n,3[англ.]	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.	Некомпактная гиперболическая
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Фигуры
Конфигурация	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойственная
Конфигурация грани	V4.6.4[англ.]	V4.6.6	V4.6.8[англ.]	V4.6.10	V4.6.12[англ.]	V4.6.14[англ.]	V4.6.16[англ.]	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Согласно построению Витхоффа имеется восемь гиперболических однородных мозаик, которые могут быть основаны на правильном семиугольном замощении.

Раскрашивая плитки красным на месте исходных гранец, жёлтым на месте исходных вершин и синим вдоль исходных рёбер, получим 8 форм.

Однородные семиугольные/треугольные мозаики[англ.]
Симметрия: [7,3], (*732)[англ.]							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	2t{7,3}[англ.]=t{3,7}	2r{7,3}	rr{7,3}[англ.]	tr{7,3}	sr{7,3}
Однородные двойственные мозаики
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14[англ.]	V3.3.3.3.7

Смотрите также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик на евклидовой плоскости