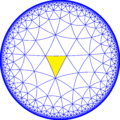
Усечённая треугольно-восьмиугольная мозаика

Усечённая треугольно-восьмиугольная мозаика — это полуправильное замощение гиперболической плоскости. В каждой вершине мозаики имеется один квадрат, один шестиугольник и один шестнадцатиугольник. Символ Шлефли мозаики — tr{8,3}.

Усечённая треугольно-восьмиугольная мозаика
Тип	Однородная гиперболическая мозаика
Конфигурация вершины	4.6.16
Символ Шлефли	tr{8,3} или ${\displaystyle t{\begin{Bmatrix}8\\3\end{Bmatrix}}}$
Символ Витхоффа	2 8 3 |
Симметрии	[8,3], (*832)
Диаграммы Коксетера — Дынкина	или
Двойственная мозаика	разделенная ромбическая мозаика порядка 3-8[англ.]
Свойства	изогональная

Симметрия

Усечённая треугольно-восьмиугольная мозаика с зеркалами

Двойственная мозаика для этой мозаики — кисромбическая мозаика порядка 3-8, и она представляет фундаментальную область симметрии [8,3] (*832). Существует 3 подгруппы малого индекса, строящиеся из [8,3] путём удаления зеркала и альтернацией. В рисунках фундаментальные области раскрашены чередующимся образом, а зеркала находятся на границах между цветами.

Подгруппа с индексом 6, построенная как [8,3^*], становится [(4,4,4)], (*444). Подгруппа с индексом 3 строится как [8,3^⅄] с удаление 2/3 голубых зеркал.

Подгруппы малого индекса группы [8,3], (*832)

Индекс	1	2		3	6
Диаграммы
Коксетер (орбифолд)	[8,3] = (*832)	[1+,8,3] = = (*433)	[8,3+] = (3*4)	[8,3⅄] = = (*842)	[8,3*] = = (*444)
Прямые подгруппы
Index	2	4		6	12
Диаграммы
Коксетер (орбифолд)	[8,3]+ = (832)	[8,3+]+ = = (433)		[8,3⅄]+ = = (842)	[8,3*]+ = = (444)

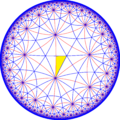
Кисромбическая мозаика порядка 3-8

Кисромбическая мозаика порядка 3-8
Тип	Двойственная полурегулярная гиперболическая мозаика
Конфигурация грани	V4.6.16
Грани	Прямоугольный треугольник
Симметрии	[8,3], (*832)
Группа вращения	[8,3]+, (832)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	Усечённая треугольно-восьмиугольная мозаика
Свойства	гранетранзитивная

Кисромбическая мозаика порядка 3-8 — это полуправильная двойственная мозаика на гиперболической плоскости. Она состоит из конгруэнтных прямоугольных треугольников с 4, 6 и 16 треугольниками в вершинах.

Изображение показывает проекцию гиперболической плоскости на дисковую модель Пуанкаре.

Мозаика обозначается V4.6.16, поскольку каждая треугольная грань (прямоугольный треугольник) имеет три типа вершин — одна с 4 треугольниками, одна с 6 треугольниками и одна с 16 треугольниками. Мозаика является двойственной мозаикой^[англ.] для усечённой треугольно-восьмиугольной мозаики, которая имеет в каждой вершине один квадрат, один шестиугольник и один шестнадцатиугольник..

Название

Альтернативным названием является 3-8 kisrhombille (3-8 кисромбический паркет), данное Конвеем. Конвей рассматривал данное замощение как 3-8 ромбическую мозаику, разделённую оператором kis, который добавляет центральную точку в каждый ромб и делит его на четыре треугольника.

Связанные многогранники и замощения

Эта мозаика является одной из 10 однородных мозаик, построенных из гиперболической симметрии [8,3] и трёх подсимметрий [1⁺,8,3], [8,3⁺] и [8,3]⁺.

Однородные восьмиугольные/треугольные мозаики
Симметрия: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								или	или
Однородные двойственные
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

Эта мозаика может считаться членом последовательности однородных объектов с вершинной фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются всеусечёнными^[англ.] многогранники (зоноэдры), показанные ниже как сферические мозаики. Для p > 6 членам последоавательности являются замощения гиперболической плоскости, начиная с усечённой треугольно-семиугольной мозаики.

*n32 мутации по симметрии полностью усечённых мозаик: 4.6.2n

Симметрия *n32[англ.] n,3[англ.]	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.	Некомпактная гиперболическая
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Фигуры
Конфигурация	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойственная
Конфигурация грани	V4.6.4[англ.]	V4.6.6	V4.6.8[англ.]	V4.6.10	V4.6.12[англ.]	V4.6.14[англ.]	V4.6.16[англ.]	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Смотрите также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Разделенная ромбическая мозаика
• Список однородных мозаик на евклидовой плоскости
• Однородные мозаики на гиперболической плоскости