Wythoffov simbol

Wythoffov simbol so prvi uporabili Harold Scott MacDonald Coxeter (1907–2003), Hugh Christopher Longuet-Higgins (1923–2004) in Miller v svojih pregledih uniformnih poliedrov. Predstavlja način uporabe Wythoffove konstrukcije z uporabo Schwarzevih trikotnikov

Schwartzov trikotnik je trikotnik, ki z lastnimi odboji na robovih, pokrije neskončno krat sfero ali ravnino. Običajni zapis za trikotnik so tri števila (cela števila ali ulomki) tako, da je π/x kot v enem izmed oglišč. Za zgled naj nam služi trikotnik (2 3 4) s simetrijo kocke, vrednosti (5/2 5/2 5/2) pa pomenijo stransko ploskev ikozaedra.

Wythoffova konstrukcija v treh razsežnostih sestavlja izbira točke v trikotniku katere razdalja do vsake izmed stranic, če je neničelna, je enaka in pada pravokotno na vsak rob.

Vsaka stranica trikotnika se imenuje po nasprotnem kotu. Tako je stranica nasproti pravemu kotu označena z '2'. Simbol tako predstavlja izključeno|vključeno. Vsako od števil p v simbolu postane mnogokotnik pn, kjer je n število drugih robov, ki nastopajo pred črtico. Tako je v 3 | 4 2 oglišče točka postane degenerirani mnogokotnik s stranicami 3x0 leži v kotu π/3 trikotnika in višino od tega vogala lahko smatramo kot, da tvori polovico meje med kvadratom (ima 4x1 stranic) in dvokotnikom (ima 2x1 stranic) z ničelno površino.

Posebni primer za snub-oblike, ki imajo simbol | p q r, lahko postavimo oglišče v središče sfere. Stranske ploskve prirezane oblike se izmenjujejo kot p 3 q 3 r 3. Iz tega se dobi antiprizmo, ko je q=r=2.

Vsak simbol predstavlja uniformni polieder ali tlakovanje, čeprav imajo nekatera tlakovanja in poliedri različne Wythoffove simbole za različne generatorje simetrije. Zgledi: pravilna kocka ima simbol enak 3 | 4 2 s simetrijo O_h. Kvadratna prizma z dvema barvama ima Wythofov simbol 2 4 | 2 . Simetrija D_4h s tremi barvami ima Wythoffov simbol 2 2 2 |.

Skupna preglednica

Osem oblik Wythoffove konstrukcije iz splošnega trikotnika (p q r).

Obstaja sedem točk generiranja za vsako od množic p, q, r (in nekaj posebnih oblik)

splošno			pravokotni trikotnik (r=2)
opis	Wythoffov simbol	konfiguracija oglišč	Wythoffov simbol	konfiguracija oglišč	Schläflijev simbol
pravilen in kvazipravilen	q | p r	(p.r)q	q | p 2	pq	{p,q}
	p | q r	(q.r)p	p | q 2	qp	{q,p}
	r | p q	(q.p)r	2 | p q	(q.p)²	t1{p,q}
prisekan in razširjen	q r | p	q.2p.r.2p	q 2 | p	q.2p.2p	t0,1{p,q}
	p r | q	p.2q.r.2q	p 2 | q	p. 2q.2q	t0,1{q,p}
	p q | r	2r.q.2r.p	p q | 2	4.q.4.p	t0,2{p,q}
parne stranske ploskve	p q r |	2r.2q.2p	p q 2 |	4.2q.2p	t0,1,2{p,q}
	p q (r s) |	2p.2q.-2p.-2q	p 2 (r s) |	2p.4.-2p.4/3
prirezan	| p q r	3.r.3.q.3.p	| p q 2	3.3.q.3.p	s{p,q}
	| p q r s	(4.p.4.q.4.r.4.s)/2	-	-

Obstajajo trije posebni primeri:

• p q (r s) | – to je mešanica p q r | in p q s |.
• | p q r – prirezane (snub) oblike uporabljajo ta simbol, ki se sicer ne uporablja.
• | p q r s – edinstvena prirezana oblika za U75, ki ga ne moremo konstruirati po Wythoffu.

Opis

Števila p, q, r opisujejo osnovni trikotnik grupe simetrije: na njegovih ogliščih se generirajoča zrcala srečajo v kotih π/p, π/q, π/r. na sferi so trije glavni tipi simetrije (3 3 2), (4 3 2) in (5 3 2) in neskončna družina (p 2 2) za poljuben p.

Položaj vertikalne črtice v simbolu določa določen položaj točke generiranja v osnovnem trikotniku. Točka generiranja je lahko vključena ali izključena oziroma aktivirana ali neaktivirana. To razlikovanje kreira 8 (2³) možnih oblik. Pri tem smo zanemarili primer, ko je točka generiranja na vseh zrcalih.

V tej notaciji so zrcala označena z redom odboja nasprotnega oglišča. Vrednosti p,q,r, ki se nahajajo pred vertikalno črto pripadajo aktivnim zrcalom.

Nemogoč simbol v obliki | p q r pove, da so vse točke na zrcalih. To pa je možno samo, če so trikotniki degenerirani oziroma zmanjšani v točko. Ta neuporabljen simbol se torej koristi za predstavitev primera, ko so vsa zrcala aktivna. Pri tem so vsi neparni odboji izpuščeni. Rezultirajoča slika ima samo vrtilno (rotacijsko) simetrijo.

Ta simbol je funkcionalno podoben splošnejšemu Coxeter-Dinkinovemu diagramu. V njem vsak vozel predstavlja zrcalo in loke med njimi. Loke označimo s števili. Pomenijo pa kote med zrcali. Vozel obdamo s krogcem, če točka ni na zrcalu.

Trikotniki simetrije

Znani so 4 simetrijski razredi zrcaljenja na sferi, in dva v evklidski ravnini. Nekaj teh neskončno mnogih vzorcev v hiperbolični ravnini je tudi prikazanih.

• (p 2 2) diedrska simetrija, p = 2, 3, 4... (red 4p)
• (3 3 2) tetraedrska simetrija (reda 24)
• (3 3 3) *333 simetrija (evklidska ravnina)
• (4 3 2) oktaedrska simetrija (reda 48)
• (4 3 3) *433 simetrija (hiperbolična ravnina)
• (4 4 2) *442 simetrija: trikotnik 45°-45°-90°
• (4 4 3) *443 simetrija (hiperbolična ravnina)
• (5 3 2) ikozaedrska simetrija (reda 120)
• (5 4 2) *542 simetrija (hiperbolična ravnina)
• (6 3 2) *632 simetrija: trikotnik 30°-60°-90°
• (7 3 2) *732 simetrija (hiperbolična ravnina)

diedrska sferna		sferna
D2h	D3h	Td	Oh	Ih
*222	*322	*332	*432	*532
(2 2 2)	(3 2 2)	( 3 3 2)	(4 3 2)	(5 3 2)

Zgornje grupe simetrije vključujejo samo celoštevilčne rešitve na sferi. Seznam Schwarzevih trikotnikov vključuje racionalna števila in določa celotno množico rešitev nekonveksnih uniformnih poliedrov.

evklidska ravnina

p4m	p3m	p6m
*442	*333	*632
(4 4 2)	(3 3 3)	(6 3 2)

hiperbolična ravnina

*732	*542	*433
(7 3 2)	(5 4 2)	(4 3 3)

V zgornjih tlakovanjih predstavlja vsak trikotnik osnovno domeno in je pobarvan s parnimi in neparnimi odboji.

Celotno sferno in ravninsko tlakovanje

Izbrana tlakovanja so kreirana z Wythoffovo konstrukcijo in so prikazana spodaj.

Sferno tlakovanje (r = 2)

(p q 2)	osnovni trikotniki	starševsko telo	prisekan	rektificiran	dvojno prisekan	dvojno rektificiran (dualen)	kanteliran	omniprisekan (kantiprisekan)	prirezan
Wythoffov simbol		q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Schläflijev simbol		t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Coxeter-Dinkinov diagram
konfiguracija oglišč		pq	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	qp	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
tetraedrsko (3 3 2)		{3,3}	(3.6.6)	(3.3a.3.3a)	(3.6.6)	{3,3}	(3a.4.3b.4)	(4.6a.6b)	(3.3.3a.3.3b)
oktaedrsko (4 3 2)		{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4a.4)	(4.6.8)	(3.3.3a.3.4)
ikozaedrsko (5 3 2)		{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3a.3.5)

Diedrska simetrija (q = r = 2)

Sferno tlakovanje z diedrsko simetrijo obstaja za vse p = 2, 3, 4, ... mnogi so z dvokotniškimistranskimi ploskvami, ki postanejo degenerirani poliedri. Dve od osmih oblik (rektificirana in kantelirana) so ponovitve in so v preglednici izpuščene.

(p 2 2)	osnovni trikotniki	starševsko telo	prisekan	dvojno prisekan (prisekan dualen)	dvojno rektificiran (dualen)	omniprisekan (kantiprisekan)	prirezan
razširjeni Schläflijev simbol		${\displaystyle {\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\2\end{Bmatrix}}}$
		t0{p,2}	t0,1{p,2}	t1,2{p,2}	t2{p,2}	t0,1,2{p,2}	s{p,2}
Wythoffov simbol		2 | p 2	2 2 | p	2 p | 2	p | 2 2	p 2 2 |	| p 2 2
Coxeter–Dinkinov diagram
konfiguracija oglišč		p²	(2.2p.2p)	(p.p)	2p	(4.2p.4)	(3.3.p. 3)
(2 2 2)		{2,2}	2.4.4	4.4.2	{2,2}	4.4.4	3.3.3.2
(3 2 2)		{3,2}	2.6.6	4.4.3	{2,3}	4.4.6	3.3.3.3
(4 2 2)		{4,2}	2.8.8	4.4.4	{2,4}	4.4.8	3.3.3.4
(5 2 2)		{5,2}	2.10.10	4.4.5	{2,5}	4.4.10	3.3.3.5
(6 2 2)		{6,2}	2.12.12	4.4.6	{2,6}	4.4.12	3.3.3.6
...

Ravninska tlakovanja (r = 2)

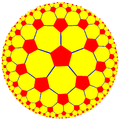
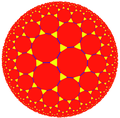
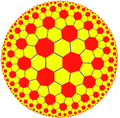
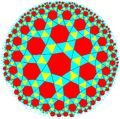
Prikazana so nekatera značilna hiperbolična tlakovanja kot projekcija na Poincaréjevem disku.

(p q 2)	osnovni trikotnik	starševsko telo	prisekan	rektificiran	dvojno prisekan	dvojno rektificiran (dualen)	kanteliran	omniprisekan (kantiprisekan)	prirezan
Wythoffov simbol		q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Schläflijev simbol		t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Coxeter-Dinkinov diagram
konfiguracija oglišč		pq	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	qp	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
kvadratno tlakovanje (4 4 2)	V4.8.8	{4,4}	4.8.8	4.4a.4.4a	4.8.8	{4,4}	4.4a.4b.4a	4.8.8	3.3.4a.3.4b
(hiperbolična ravnina) (5 4 2)		{5,4}	4.10.10	4.5.4.5	5.8.8	{4,5}	4.4.5.4	4.8.10	3.3.4.3.5
(hiperbolična ravnina) (5 5 2)		{5,5}	5.10.10	5.5.5.5	5.10.10	{5,5}	4.4.5.4	4.10.10	3.3.5.3.5
šestkotno tlakovanje (6 3 2)	V4.6.12	{6,3}	3.12.12	3.6.3.6	6.6.6	{3,6}	3.4.6.4	4.6.12	3.3.3.3.6
(hiperbolična ravnina) (7 3 2)		{7,3}	3.14.14	3.7.3.7	7.6.6	{3,7}	3.4.7.4	4.6.14	3.3.3.3.7
(hiperbolična ravnina) (8 3 2)		{8,3}	3.16.16	3.8.3.8	8.6.6	{3,8}	3.4.8.4	4.6.16	3.3.3.3.8
(hiperbolična ravnina) (∞ 3 2)
(hiperbolična ravnina) (∞ 4 2)
(hiperbolična ravnina) (∞ ∞ 2)

Ravninska tlakovanja (r > 2)

Coxeter-Dinkinov diagram je podan v linearni obliki, čeprav je v resnici trikotnik, ki ima zadnji segment povezan s prvim vozlom.

Wythoffov simbol (p q r)	osnovni trikotniki	q | p r	r q | p	r | p q	r p | q	p | q r	p q | r	p q r |	| p q r
Coxeter-Dinkinov diagram
konfiguracija oglišč		(p.q)r	(r.2p.q.2p)	(p.r)q	(q.2r.p. 2r)	(q.r)p	(p. 2q.r.2q)	(2p.2q.2r)	(3.r.3.q.3.p)
evklidski (3 3 3)		(3.3)3	3.6.3.6	(3.3)3	3.6.3.6	(3.3)3	3.6.3.6	6.6.6	3.3.3.3.3.3
hiperbolični (4 3 3)		(3.4)³	3.8.3.8	(3.4)³	3.6.4.6	(3.3)4	3.6.4.6	6.6.8	3.3.3.3.3.4
hiperbolični (4 4 3)		(3.4)4	3.8.4.8	(3.4)4	3.6.4.6	(3.4)4	4.6.4.6	6.8.8	3.3.3.4.3.4
hiperbolični (4 4 4)		(4.4)4	4.8.4.8	(4.4)4	4.8.4.8	(4.4)4	4.8.4.8	8.8.8	3.4.3.4.3.4
hiperbolični (3 3 ∞)
hiperbolični (3 ∞ ∞)
hiperbolični (∞ ∞ ∞)

Prekrivajoča se sferna tlakovanja (r = 2)

Tlakovanja so prikazana kot poliedri. Nekaj oblik je degeneriranih. Te so prikazane z oklepaji za slike oglišč, s prekrivajočimi se robovi ali oglišči.

(p q 2)	osnovni trikotnik	starševsko telo	prisekan	rektificiran	dvojno prisekan	dvojno prisekan (dualen)	kanteliran	omniprisekan (kantiprisekan)	prirezan
Wythoffov simbol		q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Schläflijev simbol		t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Coxeter-Dinkinov diagram
konfiguracija oglišč		pq	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	qp	(p. 4.q.4)	(4.2p.2q)	(3.3.p. 3.q)
ikozaedersko (5/2 3 2)		{3,5/2}	(5/2.6.6)	(3.5/2)2	[3.10/2.10/2]	{5/2,3}	[3.4.5/2.4]	[4.10/2.6]	(3.3.3.3.5/2)
ikozaedersko (5 5/2 2)		{5,5/2}	(5/2.10.10)	(5/2.5)2	[5.10/2.10/2]	{5/2,5}	(5/2.4.5.4)	[4.10/2.10]	(3.3.5/2.3.5)

Glej tudi

• pravilni politop
• pravilni polieder
• seznam uniformnih tlakovanj
• seznam uniformnih poliedrov

Zunanje povezave

• Weisstein, Eric Wolfgang. »Wythoff Symbol«. MathWorld.
• Wythoffov simbol (angleško)