正多面體列表

在幾何學中，正多面體是指各面都是全等的正多邊形且每一個頂點所接的面數都是一樣的多面體。除了五種凸正多面體（柏拉圖立體）外，亦有其他能符合上述條件的立體，例如四種星形正多面體（克卜勒－龐索立體）^[2]。

部分的正多面體

主條目：正多面體

在不考慮其他空間（如雙曲空間、複數空間）的情況下，麥克馬倫在其論文中共整理並列出了48種正多面體^[3]。

概述

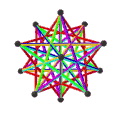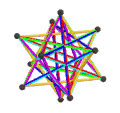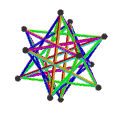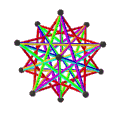
所有正多面體皆可以使用施萊夫利符號來表示，其可以計為{n, m}。其中n表示構成面的頂點數，m則表示與頂點相鄰的多邊形數量。在中文語境中，一般被大眾認知的正多面體通常代表只有五種的凸正多面體，又稱為柏拉圖立體，其包括了正四面體、立方體、正八面體、正十二面體和正二十面體^[4]。然而在定義上，正多面體僅指每個面是正多邊形、每條邊等長每個角等角且每面全等的多面體，而符合上述定義的多面體不一定是凸多面體，也可能是星形多面體^[5]、抽象多面體^[6]或扭歪多面體^[7]等。這些多面體除了五種凸正多面體外，還有四種非凸正多面體（克普勒–龐索立體）、五種抽象正多面體和五種複合正多面體。

柏拉圖立體	正四面體、 立方體、 正八面體、 正十二面體、 正二十面體
克卜勒－龐索立體	小星形十二面體、 大十二面體、 大星形十二面體、 大二十面體
複合正多面體	星形八面體、 五複合正四面體、 十複合正四面體、 五複合立方體、 五複合正八面體
正扭歪無限面體	四角六片四角孔扭歪無限面體、 六角四片四角孔扭歪無限面體、 六角六片三角孔扭歪無限面體
正扭歪多面體	四角六片三角孔扭歪正三十面體、 六角四片三角孔扭歪正二十面體、 四角八片三角孔扭歪正二百八十八面體、 八角四片三角孔扭歪正一百四十四面體
複空間正多面體	黑塞二十七面體、 雙黑塞二十七面體、 截半黑塞二十七面體
正多面體半形	立方體半形、 八面體半形、 十二面體半形、 二十面體半形
依面的個數	正零面體（0、 空多胞形）、 正一面體（1）、 正二面體（2、 多邊形二面體）、 正三面體（3、 立方體半形）、 正四面體（4、 正四面體、 八面體半形）、 正六面體（6、 立方體、 十二面體半形）、 正八面體（8、 正八面體、 星形八面體）、 正十面體（10、 二十面體半形）、 正十二面體（12、 正十二面體、 小星形十二面體、 大十二面體、 大星形十二面體）、 正二十面體（20、 正二十面體、 大二十面體、 六角四片三角孔扭歪正二十面體、 五複合正四面體）、 正二十七面體（27、 黑塞二十七面體）、 正三十面體（30、 四角六片三角孔扭歪正三十面體、 五複合立方體）、 正四十面體（40、 十複合正四面體、 五複合正八面體）、 正五十四面體（54、 截半黑塞二十七面體）、 正七十二面體（72、 雙黑塞二十七面體）、 正一百四十四面體（144、 八角四片三角孔扭歪正一百四十四面體）、 正二百八十八面體（288、 四角八片三角孔扭歪正二百八十八面體）、 正無限面體（∞、 正鑲嵌圖、 扭歪無限面體、 § 雙曲無限面體）
依組成面	§ 二角形、 § 正三角形、 § 正方形、 § 五邊形 （ § 五邊形、 § 正五角星形）、 § 六邊形、 § 七邊形、 § 八邊形、 § 無限邊形

列表

下表列出了所有標記可以在其對稱性上遞移的多面體，換句話說，即該多面體皆同時具有等邊、等角和等面的特性。

分類	名稱 施氏符號	子類	圖像	頂點	邊	面	面的位置	頂點圖	X	對偶多面體	對稱性
凸正 多面體 柏拉圖立體	正四面體 {3,3}4	四面體		4	6條稜	4個正三角形		33	2	（自身對偶）	Td [3,3] (*332)
	立方體 {4,3}6	六面體		8	12條稜	6個正方形		43	2	正八面體	Oh [4,3] (*432)
	正八面體 {3,4}6	八面體		6	12條稜	8個正三角形		34	2	立方體	Oh [4,3] (*432)
	正十二面體 {5,3}10	十二面體		20	30條稜	12個正五邊形		53	2	正二十面體	Ih [5,3] (*532)
	正二十面體 {3,5}10	二十面體		12	30條稜	20個正三角形		35	2	正十二面體	Ih [5,3] (*532)
星形 正多面體 克卜勒 龐索立體	小星形十二面體 {5/2,5}6	十二面體		12	30條稜	12個正五角星		(5/2)5	-6	大十二面體	Ih [5,3] (*532)
	大十二面體 {5,5/2}6	十二面體		12	30條稜	12個正五邊形		(55)/2	-6	小星形十二面體	Ih [5,3] (*532)
	大星形十二面體 {5/2,3}10/3	十二面體		20	30條稜	12個正五角星		(5/2)3	2	大二十面體	Ih [5,3] (*532)
	大二十面體 {3,5/2}10/3	二十面體		12	30條稜	20個正三角形		(35)/2	2	大星形十二面體	Ih [5,3] (*532)
複合正多面體	星形八面體 {{3,3}}、 a{4,3} ß{2,4}、 ßr{2,2} ∪ 、 、 、	星形八面體 二複合四面體		8	12條稜	8個正三角形			4	（自身對偶）	Oh [4,3]
	五複合正四面體	星形二十面體		20	30條稜	20個正三角形			10	（自身對偶）	手性（英語：Chirality (mathematics)） 二十面 體群（英語：Icosahedral symmetry） (I)
	十複合正四面體 2{5,3}[10{3,3}]2{3,5}[8]	星形四十面體		20	60條稜	40個正三角形			0	（自身對偶）	${\displaystyle I_{h}}$群
	五複合立方體 2{5,3}[5{4,3}][9][8]	星形三十面體		20	60條稜	30個正方形			-10	五複合正八面體	${\displaystyle I_{h}}$群
	五複合正八面體 [5{3,4}]2{3,5}[9][8]	星形四十面體		30	60條稜	40個正三角形			10	五複合立方體	${\displaystyle I_{h}}$群
正扭歪 無限面體	四角六片四角孔 扭歪無限面體 {4,6|4}	扭歪無限面體		∞	∞條稜	正方形 孔洞： 正方形		{3}#{ }		六角四片 四角孔 扭歪 無限面體	[[4,3,4]] [[4,3,4]+]
	六角四片四角孔 扭歪無限面體 {6,4|4}	扭歪無限面體		∞	∞條稜	正六邊形 孔洞： 正方形		{4}#{ }		四角六片 四角孔 扭歪 無限面體	[[4,3,4]] [[4,3,4]+]
	六角六片三角孔 扭歪無限面體 {6,6|3}	扭歪無限面體		∞	∞條稜	正六邊形 孔洞： 正三角形		{3}#{ }		（自身對偶）	[[3[4]]] [[3[4]]+]
四維空間 扭歪正多面體	四角六片三角孔 扭歪正三十面體 {4,6|3}	扭歪三十面體		20	60條稜	30個正方形 孔洞： 正三角形		{3}#{ }	-10	六角四片 三角孔 扭歪正 二十面體
	六角四片三角孔 扭歪正二十面體 {6,4|3}	扭歪二十面體		30	60條稜	20個正六邊形 孔洞： 正三角形		{4}#{ }	-10	四角六片 三角孔 扭歪正 三十面體
	四角八片三角孔 扭歪正 二百八十八面體 {4,8|3}	扭歪288面體		144	576條稜	288個正方形 孔洞： 正三角形			-144	八角四片 三角孔 扭歪正 144面體
	八角四片三角孔 扭歪正 一百四十四面體 {8,4|3}	扭歪144面體		288	576條稜	144個正八邊形 孔洞： 正三角形			-144	四角八片 三角孔 扭歪正 288面體
	四角四片p角孔 扭歪正 一百四十四面體 {4,4|p}	扭歪p2面體		p2	2p2條稜	p2個正方形 孔洞： 正p邊形
${\displaystyle \mathbb {C} ^{3}}$複空間 正多面體	2{3}2{4}p	複p3面體		3p	3p2條稜	p3個正三角形		2{4}p
	p{4}2{3}2	複3p面體		p3	3p2條p元稜	3p個p{4}2		正三角形
	黑塞二十七面體 3{3}3{3}3	複二十七面體		27	72條3元稜	27個3{3}3		3{3}3		（自身對偶）
	雙黑塞二十七面體 2{4}3{3}3	複七十二面體		54	216條3元稜	72個2{4}3		3{3}3		截半黑塞二十七面體
	截半黑塞二十七面體 3{3}3{4}2	複五十四面體		72	216條3元稜	54個3{3}3		3{4}2（英語：3-3_duoprism#Related_complex_polygons）		雙黑塞二十七面體
實射影 平面的 正多面體 多面體半形	立方體半形 {3,3}/2 {3,3}3	抽象三面體		4	6條稜	3個正方形			1	八面體半形	${\displaystyle S_{4}}$群
	八面體半形 {3,4}/2 {3,4}3	抽象四面體		3	6條稜	4個正三角形			1	立方體半形	${\displaystyle S_{4}}$群
	十二面體半形 {5,3}/2 {5,3}5	抽象六面體		10	15條稜	6個正五邊形			1	二十面體半形	${\displaystyle A_{5}}$群
	二十面體半形 {3,5}/2 {3,5}5	抽象十面體		6	15條稜	10個正三角形			1	十二面體半形	${\displaystyle A_{5}}$群
皮特里 對偶	皮特里正四面體 {3,3}π {4,3}3	拓樸三面體		4	6條稜	3個正扭歪四邊形
	皮特里立方體 {4,3}π {6,3}4	拓樸四面體		8	12條稜	4個正扭歪六邊形
	皮特里正八面體 {3,4}π {6,4}3	拓樸四面體		6	12條稜	4個正扭歪六邊形
	皮特里正十二面體 {5,3}π {10,3}5	拓樸六面體		20	30條稜	6個正扭歪十邊形
	皮特里正二十面體 {3,5}π {10,5}3	拓樸六面體		12	30條稜	6個正扭歪十邊形
	皮特里小星形十二面體 {5/2,5}π {6,5}5/2	拓樸十面體		12	30條稜	10個正扭歪六邊形
	皮特里大十二面體 {5,5/2}π {6,5/2}5	拓樸十面體		12	30條稜	10個正扭歪六邊形
	皮特里大星形十二面體 {5/2,3}π {10/3,3}5/2	拓樸六面體		20	30條稜	6個正扭歪十角星
	皮特里大二十面體 {3,5/2}π {10/3,5/2}3	拓樸六面體		12	30條稜	6個正扭歪十角星

無窮集合的正多面體

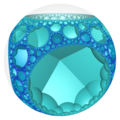
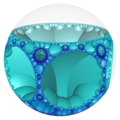
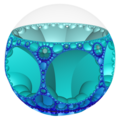
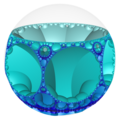
大部分的正多面體都只有有限個，如凸正多面體5個^[4]、星形多面體4個^[5]、正扭歪無限面體3個^[10]與難以良好具像化的抽象正多面體5個^[6]等。然而在部分正多面體的種類有無窮多個，如同正多邊形的邊數可以無窮上升一般，例如除了柏拉圖立體、黑塞二十七面體、雙黑塞二十七面體與截半黑塞二十七面體之外的複正多面體^[12]，或內接於雙曲仿緊空間堆砌中的極限球（英語：Horosphere）上的雙曲鑲嵌^[13]等幾何結構。

雙曲無限面體

圖為三階七邊形鑲嵌蜂巢體在三維龐加萊球體投影的結果之旋轉透視圖，其中每一個凹陷進去的弧形有稜有角部分為一個內接於雙曲空間中的超極限球上的正七邊形鑲嵌^[14]。

三階六邊形鑲嵌蜂巢體{6,3,3}中的正六邊形鑲嵌{6,3}胞。其頂點皆位於該雙曲空間極限球（英語：Horosphere）上。這時可以將這個結構視為一個雙曲空間的正多面體。

在幾何學中，平面鑲嵌可以被視為多面體的一種退化成平面的退化形式，即無限面體^[15]。然而平面鑲嵌或雙曲鑲嵌可以用類似多面體堆砌填充三為歐氏空間的方法來填滿雙曲空間，這種結構稱為蜂巢體^[16]，在這種情況下，蜂巢體中的每一個胞皆為一個平面鑲嵌或雙曲鑲嵌^[14]，即前面所述的退化多面體或無限面體^[17]。這些退化的幾何結構由於形成雙曲空間蜂巢體可以內接在一個雙曲極限球（即只與單一雙曲無窮遠點相交的雙曲空間球體）^[18]或雙曲超極限球（無法交於單一雙曲無窮遠點的雙曲空間球體）^[19]上，因此，此時也能把此結構視為一個雙曲空間的多面體，當這個多面體具有正多面體性質時，也可以稱為一種廣義的正多面體，例如六邊形鑲嵌蜂巢體中的六邊形鑲嵌^[20]或三階七邊形鑲嵌蜂巢體中的正七邊形鑲嵌^[14]。

三種平面正鑲嵌圖以及其對應的雙曲無限面體範例

鑲嵌圖	{3,6} 正三角形鑲嵌	{4,4} 正方形鑲嵌	{6,3} 正六邊形鑲嵌
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{3,6,4}（英語：Order-6-4 triangular honeycomb）	{4,4,5}（英語：Order-4-5 square_honeycomb）	{6,3,3}

正三角形組成的雙曲無限面體

鑲嵌圖	{3,6} 六階三角形鑲嵌	{3,7} 七階三角形鑲嵌	{3,8} 八階三角形鑲嵌	...	{3,∞} 無限階三角形鑲嵌
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{3,6,4 }（英語：Order-6-4 triangular honeycomb）	{3,7,3}（英語：Order-7-3 triangular honeycomb）	{3,8,3}（英語：Order-8-3 triangular honeycomb）		{3,∞,3}

正方形組成的雙曲無限面體

鑲嵌圖	{4,4} 四階正方形鑲嵌	{4,5} 五階正方形鑲嵌	{4,6} 六階正方形鑲嵌	{4,7} 七階正方形鑲嵌	{4,8} 八階正方形鑲嵌	...	{4,∞} 無限階正方形鑲嵌
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{4,4,5 }（英語：Order-4-5 square honeycomb）	{4,5,3}（英語：Order-5-3 square honeycomb）	{4,6,3}（英語：Order-6-3 square honeycomb）	{4,7,3}（英語：Order-7-3 square honeycomb）	{4,8,3}（英語：Order-8-3 square honeycomb）		{4,∞,3}

正五邊形組成的雙曲無限面體

鑲嵌圖	{5,4} 四階五邊形鑲嵌	{5,5} 五階五邊形鑲嵌	{5,6} 六階五邊形鑲嵌	{5,7} 七階五邊形鑲嵌	{5,8} （英語：Order-8 pentagonal tiling）八階五邊形鑲嵌（英語：Order-8 pentagonal tiling）	...	{5,∞} 無限階五邊形鑲嵌
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{5,4,3 }（英語：Order-4-3 pentagonal honeycomb）	{5,5,3}（英語：Order-5-3 pentagonal honeycomb）	{5,6,3}（英語：Order-6-3 pentagonal honeycomb）	{5,7,3}（英語：Order-7-3 pentagonal honeycomb）	{5,8,3}（英語：Order-8-3 pentagonal honeycomb）		{5,∞,3}

正六邊形組成的雙曲無限面體

鑲嵌圖	{6,3} 三階六邊形鑲嵌	{6,4} 四階六邊形鑲嵌	{6,5} 五階六邊形鑲嵌	{6,6} 六階六邊形鑲嵌	{6,7} 七階六邊形鑲嵌	{6,8} 八階六邊形鑲嵌	...	{6,∞} （英語：Infinite-order_hexagonal_tiling）無限階六邊形鑲嵌（英語：Infinite-order_hexagonal_tiling）
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{6,3,3}	{6,4,3}	{6,5,3}	{6,6,3}	{6,7,3}	{6,8,3}		{6,∞,3}

正七邊形組成的雙曲無限面體

鑲嵌圖	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}	...	{7,∞}
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{7,3,3}	{7,4,3}	{7,5,3}

正八邊形組成的雙曲無限面體

鑲嵌圖	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}	...	{8,∞}
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{8,3,3}	{8,4,3}	{8,5,3}

正無限邊形組成的雙曲無限面體

在雙曲空間的無限邊形又稱為超無限邊形或偽多邊形^[21]。

鑲嵌圖	{∞,3}	{∞,4}	{∞,5}	{∞,6}（英語：Order-6_apeirogonal_tiling）	{∞,7}（英語：Order-7_apeirogonal_tiling）	{∞,8}（英語：Order-8_apeirogonal_tiling）	...	{∞,∞}
以該鑲嵌圖為胞 的雙曲空間蜂巢體	{∞,3,3}	{∞,4,3}	{∞,5,3}	{∞,6,3}	{∞,7,3}	{∞,8,3}		{∞,∞,3}

多面形與多邊形二面體

參見：多面形和多邊形二面體

二角形二面體 {2,2}	正三角形二面體 {3,2}	正方形二面體 {4,2}	正五邊形二面體 {5,2}	正六邊形二面體 {6,2}	...	{n,2}
正二面形 {2,2}	正三面形 {2,3}	正四面形 {2,4}	正五面形 {2,5}	正六面形 {2,6}	...	{2,n}

依施萊夫利符號分類

施萊夫利符號	多面體	組成面	頂點圖	孔洞	皮特里多邊形
未定義	零面體	未定義	未定義	未定義	未定義
{0,0}	無邊地區圖[22]	零角形{0}	零角形{0}
{1,2}2	一角形二面體	一角形{1}	二角形{2}		二角形{2}
{2,1}2	一面形	二角形{2}	一角形{1}
{2,2}2	二面形（二角形二面體）		二角形{2}
{2,3}6	三面形		三角形{3}		六邊形{6}
{2,n}	多面形		多邊形{n}		不一定
{3,2}6	三角形二面體	三角形{3}	二角形{2}		六邊形{6}
{3,3}4	正四面體		三角形{3}		四邊形{4}
{3,4}3	正八面體半形 皮特里四面體的對偶多面體		正方形{4}		三角形{3}
{3,4}6	正八面體				六邊形{6}
{3,5}5	二十面體半形		五邊形{5}		五邊形{5}
{3,5/2}10/3	皮特里大二十面體		五角星{5/2}		十角星{10/3}
{3,5}10	正二十面體		五邊形{5}		十邊形{10}
{3,6}	正三角形鑲嵌		六邊形{6}		無限邊形
{3,6}4	皮特里立方體				正方形{4}
{3,10}5	皮特里十二面體的對偶多面體		十邊形{10}		五邊形{5}
{4,2}4	正方形二面體	正方形{4}	二角形{2}		正方形{4}
{4,3}3	立方體半形 皮特里四面體		三角形{3}		三角形{3}
{4,3}6	立方體				六邊形{6}
{4,4}	正方形鑲嵌		正方形{4}		無限邊形
{4,5}	五階正方形鑲嵌		五邊形{5}
{4,5}6	內側菱形三十面體（抽象）[23]				六邊形{6}
{4,6}	六階正方形鑲嵌		六邊形{6}		無限邊形
{4,6}3	皮特里八面體的對偶多面體				三角形{3}
{4,6|3}10	四角六片三角孔扭歪正三十面體			三角形{3}	十邊形{10}
{4,6|4}	四角六片四角孔扭歪無限面體			正方形{4}	無限邊形
{5,2}10	五邊形二面體	五邊形{5}	二角形{2}	未定義	十邊形{10}
{5,3}5	正十二面體半形		三角形{3}		五邊形{5}
{5,3}10	正十二面體				十邊形{10}
{5/2,3}10/3	大星形十二面體	五角星{5/2}			十角星{10/3}
{5,4}	四階五邊形鑲嵌	五邊形{5}	正方形{4}		無限邊形
{5,4}6	截半大十二面體（抽象）[23]				六邊形{6}
{5,5/2}6	大十二面體		五角星{5/2}
{5/2,5}6	小星形十二面體	五角星{5/2}	五邊形{5}
{5,6}4	雙三斜十二面體（抽象）[23]	抽象五邊形{5}	六邊形{6}		四邊形{4}
{5,10}3	皮特里二十面體的對偶多面體	五邊形{5}	十邊形{10}		三角形{3}
{6,2}6	六邊形二面體	六邊形{6}	二角形{2}		六邊形{6}
{6,3}	正六邊形鑲嵌		三角形{3}		無限邊形
{6,3}4	皮特里立方體的對偶多面體		三角形{3}		正方形{4}
{6,4}	四階六邊形鑲嵌		正方形{4}		無限邊形
{6,4}3	皮特里八面體		扭歪四邊形{4}		三角形{3}
{6,4|4}	六角四片四角孔扭歪無限面體		正方形{4}	正方形{4}	無限邊形
{6,5}	五階六邊形鑲嵌		五邊形{5}	未定義
{6,5}4	內側三角六邊形二十面體（抽象）[23]				四邊形{4}
{6,5}5/2	皮特里小星形十二面體				五角星{5/2}
{6,5/2}5	皮特里大十二面體		五角星{5/2}		五邊形{5}
{6,6|3}	六角六片三角孔扭歪無限面體		六邊形{6}	三角形{3}	無限邊形
{6,6}6	凹五角錐十二面體（抽象）[23]			未定義	六邊形{6}
{10,2}10	十邊形二面體	十邊形{10}	二角形{2}		十邊形{10}
{10,3}5	皮特里十二面體		三角形{3}		五邊形{5}
{10/3,3}5/2	皮特里大星形十二面體	十角星{10/3}			五角星{5/2}
{10/3,5/2}3	皮特里大二十面體		五角星{5/2}		三角形{3}
{10,5}3	皮特里二十面體	十邊形{10}	五邊形{5}

依組成面分類

一般的凸正多面體只能由正三角形、正方形和正五邊形構成；若考慮非凸的情況則可以由正五角星構成；若允許複數${\displaystyle \mathbb {C} ^{3}}$的空間，則莫比烏斯－坎特八邊形也能構成正多面體。然而正七邊形難以存在於平坦空間的立體中。^[24]而目前已知存有正七邊形的正多面體存於雙曲空間中。^[14]

二角形組成的正多面體

多面形

正二面形 {2,2} 2個二角形

正三面形 {2,3} 3個二角形

正四面形 {2,4} 4個二角形

正五面形 {2,5} 5個二角形

正六面形 {2,6} 6個二角形

...

{2,n} n個二角形

正三角形組成的正多面體

正三角形二面體 {3,2} 2個正三角形	正四面體 {3,3} 4個正三角形	八面體半形 {3,4}/2 4個正三角形	正八面體 {3,4} 8個正三角形	星形八面體 2{3,3} 8個正三角形	二十面體半形 {3,5}/2 10個正三角形	正二十面體 {3,5} 20個正三角形
大二十面體 {3,5/2} 20個正三角形	五複合正四面體 5{3,3} 20個正三角形	十複合正四面體 10{3,3} 40個正三角形	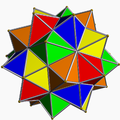五複合正八面體 5{3,4} 40個正三角形	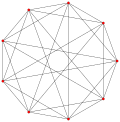2{3}2{4}p p3個正三角形	正三角形鑲嵌 {3,n} 無窮個正三角形

正方形組成的正多面體

正方形二面體 {4,2} 2個正方形

立方體半形 {4,3}/2 3個正方形

立方體 {4,3} 6個正方形

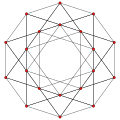扭歪正三十面體 {4,6|3} 30個正方形

五複合立方體 5{4,3} 30個正方形

扭歪288面體 {4,8|3} 288個正方形

扭歪p2面體 {4,4|p} p2個正方形

多立方體 {4,6|4} 無窮個正方形

正方形鑲嵌 {4,n} 無窮個正方形

五邊形組成的正多面體

形狀	正五邊形二面體 {5,2}	十二面體半形 {5,3}/2	正十二面體 {5,4}	大十二面體 {5,5/2}	大星形十二面體 {5/2,3}
面的組成	2個正五邊形	6個正五邊形	12個正五邊形	12個正五邊形	12個正五角星形
形狀	小星形十二面體 {5/2,5}	抽象正二十四面體[23] {5,4}6	抽象正二十四面體 {5,6}4	五邊形鑲嵌 {5,n}
面的組成	12個正五角星形	24個抽象正五邊形 具像化由： 12個正五邊形和 12個正五角星形	24個抽象正五邊形 具像化由： 12個正五邊形和 12個正五角星形	無窮個正五邊形

六邊形組成的正多面體

六邊形二面體 {6,2} 2個正六邊形

扭歪二十面體 {6,4|3} 20個正六邊形

多八面體 {6,4|4} 無窮個正六邊形

多四面體 {6,6|3} 無窮個正六邊形

正六邊形鑲嵌 {6,n} 無窮個正六邊形

七邊形組成的正多面體

雙曲正七邊形鑲嵌。

參見：§ 正七邊形組成的雙曲無限面體

在實數空間的歐幾里得空間（平坦空間）中，正七邊形無法構成正多面體^[25]。由正七邊形組成的正多面體（如三階七邊形鑲嵌蜂巢體中的正七邊形鑲嵌形狀的胞）只能存於雙曲空間中^[14]。

八邊形組成的正多面體

參見：§ 正八邊形組成的雙曲無限面體

在實數空間的歐幾里得空間（平坦空間）中，正八邊形無法構成正多面體，更精確地說，即多邊形邊數超過5的正多邊形（如正六邊形、正七邊形、正八邊形等）皆無法組成正多面體，這個觀點在歐幾里得的《幾何原本》中給出了證明^[4]（參見柏拉圖立體 § 幾何證明）。因此由正八邊形組成的正多面體只能存於其他空間中，如雙曲空間中正八邊形鑲嵌形狀的胞、部分視為球面多面體的球面鑲嵌（如正八邊形二面體）以及複空間中的一種由8條三元邊和8個頂點構成的多邊形（莫比烏斯－坎特八邊形^[26]）可以構成2種複空間正多面體。^[27][28]

形狀	正八邊形二面體 {8,2}	黑塞二十七面體 3{3}3{3}3	截半黑塞二十七面體 3{3}3{4}2	八邊形鑲嵌 {8,n}
面的組成	2個正八邊形	27個正莫比烏斯－坎特八邊形	54個正莫比烏斯－坎特八邊形	無窮個正八邊形

相關多面體

柏拉圖立體可以透過康威變換轉換成13種阿基米德立體^[29]，其他正多面體也可以透過康威變換轉換成半正多面體或均勻多面體：

原像	康威變換
	截角	截半	截稜	過截角	對偶	對偶複合	小斜方截半	大斜方截半	扭稜	加錐	會合
正四面體	t0,1{3,3}	t1{3,3}	c{3,3}	t1,2{3,3}	t2{3,3}	2{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}	三角化	三角化會合
立方體	t0,1{4,3}	t1{4,3}	c{4,3}	t1,2{4,3}	t2{4,3}	{4,3}{3,4}	t0,2{4,3}	t0,1,2{4,3}	sr{4,3}	四角化	四角化會合
正八面體	t0,1{3,4}	t1{3,4}	c{3,4}	t1,2{3,4}	t2{3,4}	{3,4}{4,3}	t0,2{3,4}	t0,1,2{3,4}	sr{4,3}	三角化	三角化會合
正十二面體	t0,1{5,3}	t1{5,3}	c{5,3}	t1,2{5,3}	t2{5,3}	{5,3}{3,5}	t0,2{5,3}	t0,1,2{5,3}	sr{5,3}	五角化	五角化會合
正二十面體	t0,1{3,5}	t1{3,5}	c{3,5}	t1,2{3,5}	t2{3,5}	{3,5}{5,3}	t0,2{5,3}	t0,1,2{5,3}	sr{5,3}	三角化	三角化會合
大十二面體	t0,1{5,5/2}	t1{5,5/2}	c{5,5/2}	t1,2{5,5/2}	t2{5,5/2}	{5,5/2}{5/2,5}	t0,2{5,5/2}	t0,1,2{5,5/2}	sr{5/2,5}		五角化會合
小星形十二面體	t0,1{5/2,5}	t1{5/2,5}	c{5/2,5}	t1,2{5/2,5}	t2{5/2,5}	{5/2,5}{5,5/2}	t0,2{5/2,5}	t0,1,2{5/2,5}	sr{5/2,5}	五角化	五角化會合
大二十面體	t0,1{3,5/2}	t1{3,5/2}	c{3,5/2}	t1,2{3,5/2}	t2{3,5/2}	{3,5/2}{5/2,3}	t0,2{3,5/2}	t0,1,2{3,5/2}	sr{5/2,3}		五角化會合
大星形十二面體	t0,1{5/2,3}	t1{5/2,3}	c{5/2,3}	t1,2{5/2,3}	t2{5/2,3}	{5/2,3}{3,5/2}	t0,2{5/2,3}	t0,1,2{5/2,3}	sr{5/2,3}	五角化	五角化會合
星形八面體	t0,1(2{3,3})			t1,2(2{3,3})	t2(2{3,3})
黑塞二十七面體		t1(3{3}3{3}3)			t2(3{3}3{3}3)

備註：粗體或灰底表示變換完的結果仍為正多面體者。

參見

• 正圖形列表
• 正多面體