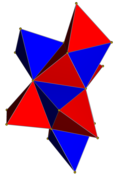
Тетраэдрально-октаэдральные соты

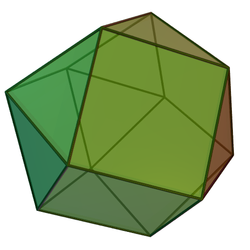
Тетраэдрально-октаэдральные соты или чередующиеся кубические соты — это квазирегулярная заполняющее пространство замощение (или соты) в трёхмерном евклидовом пространстве. Соты составлены из чередующихся октаэдров и тетраэдров в пропорции 1:2.

Чередующиеся кубические соты
Тип	Выпуклые однородные соты[англ.]
Семейство	Чередующиеся гиперболические соты[англ.] симлектические соты[англ.]
Обозначение[1]	J21,31,51, A2 W9, G1
Символы Шлефли	h{4,3,4} {3[4]} ht0,3{4,3,4} h{4,4}h{∞} ht0,2{4,4}h{∞} h{∞}h{∞}h{∞} s{∞}s{∞}s{∞}
Диаграммы Коксетера	= = = =
Ячейки	{3,3} , {3,4}
Типы граней	Треугольник {3}
Фигура ребра	[{3,3}.{3,4}]2 (прямоугольник)
Вершинная фигура	(кубооктаэдр)
Группа симметрии	Fm3m (225)
Группа Коксетера	${\displaystyle {\tilde {B}}_{3}}$, [4,31,1]
Двойственные	Додекаэдральная ячейка Ромбододекаэдральные соты Ячейка:
Свойства	вершинно-транзитивная, рёберно-транзитивная, квазиправильная мозаика

Встречаются другие названия этих сот — half cubic honeycomb (полукубические соты), half cubic cellulation (полукубическая ячеистая структура), или tetragonal disphenoidal cellulation (тетрагональная дисфеноидальная ячеистая структура). Джон Хортон Конвей назвал эти соты tetroctahedrille, а двойственные соты назвал dodecahedrille.

Ричард Бакминстер Фуллер скомбинировал два слова octahedron (октаэдр) и tetrahedron (тетраэдр) в одно octet, то есть ромбоэдр, состоящий из одного октаэдра (или двух квадратных пирамид) и двух противоположных тетрэдров.

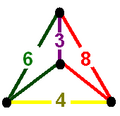
Тетраэдрально-октаэдральные соты вершинно транзитивны и имеют 8 тетраэдров и 6 октаэдров вокруг каждой вершины. Они также рёберно транзитивны и имеют 2 тетраэдра и 2 октаэдра, чередующихся вокруг каждого ребра.

Соты в геометрии — это заполняющие пространство многогранные (в любой размерности) ячейки, так что между ячейками не остаётся свободного пространства. Соты являются примером общего математического понятия замощения в пространствах любой размерности.

Соты обычно предполагаются в обычном евклидовом («плоском») пространстве, как, например, выпуклые однородные соты^[англ.]. Однако, их можно построить и в неевклидовых пространствах, как, например, гиперболические однородные соты^[англ.]. Любой конечный однородный многогранник можно спроецировать на его описанную сферу для получения однородных сот на сферическом пространстве.

Тетраэдрально-октаэдральные соты принадлежат бесконечному семейству однородных сот^?!, называющихся чередующимися гиперболическими сотами^[англ.], которые образованы путём альтернирования^[англ.] (альтернирование — это частичное усечение многогранника, при котором отрезается часть вершин) гиперболических сот и имеющих грани в виде полугиперкубов и гипероктаэдров. Соты принадлежат также другому бесконечному семейству однородных сот, называемых симлектическими сотами^[англ.].

При альтернировании кубических сот в трёхмерном пространстве кубические ячейки превращаются в тетраэдры, а на месте удалённых вершин образуются октаэдральные пустоты. В таком виде их можно представить расширенным символом Шлефли h{4,3,4} как содержащие половину вершин кубических сот {4,3,4}.

Имеются похожие соты с названием повёрнутые тетраэдрально-октаэдральные соты^[англ.]*, которые имеют слои, повёрнутые на 60 градусов, так что половина сторон имеет смежные, а не чередующиеся тетраэдры и октаэдры.

Тетраэдрально-октаэдральные соты могут иметь удвоенную симметрию, если разместить тетраэдры в октаэдральных ячейках, создавая неоднородные соты, состоящие из тетраэдров и октаэдров (как треугольные антипризмы). Вершинная фигура этих сот — усечённый триакистетраэдр порядка 3^[англ.]. Эти соты двойственны триакис усечённым тетраэдральным сотам^[англ.] с ячейками в виде триакис усечённых тетраэдров^[англ.].

Декартовы координаты

Для альтернировнных кубических сот с рёбрами, параллельными осям, и имеющими длину 1, декартовы координаты вершин равны: (для всех целочисленных значений i,j,k, для которых i+j+k чётно)

(i, j, k)

Рисунок показывает в разобранном виде^[англ.] ячейки, окружающие каждую вершину.

Симметрия

Есть два зеркальных построения и много построений альтернированием кубических сот. Примеры:

Симметрия	${\displaystyle {\tilde {B}}_{3}}$, [4,31,1] = ½${\displaystyle {\tilde {C}}_{3}}$, [1+,4,3,4]	${\displaystyle {\tilde {A}}_{3}}$, [3[4]] = ½${\displaystyle {\tilde {B}}_{3}}$, [1+,4,31,1]	[[(4,3,4,2+)]]	[(4,3,4,2+)]
Пространственная группа	Fm3m (225)	F43m (216)	I43m (217)	P43m (215)
Рисунок
Типы тетраэдров	1	2	3	4
Диаграмма Коксетера — Дынкина	=	= =

Срезы альтернированных кубических сот

Альтернированные кубические соты можно расслоить на секции, когда новые квадратные грани создаются внутри октаэдра. Каждый слой содержит квадратные пирамиды с основаниями на верхней и нижней плоскостях и тетраэдров, сидящих на боковых рёбрах этих пирамид. Другое направление среза не нуждается в дополнительных гранях и включает поочерёдно тетраэдры и октаэдры. Эти слоёные соты являются равнобедренными сотами^[англ.], а не однородными.

Проекция по свёртке

Чередующиеся кубические соты можно ортогонально спроецировать на плоскую квадратную мозаику с помощью операции геометрической свёртки, которая отображает одну пару отражений в другую. Проекция альтернированых кубических сот создаёт две копии квадратной мозаики расположения вершин^[англ.]:

Группа Коксетера	${\displaystyle {\tilde {A}}_{3}}$	${\displaystyle {\tilde {C}}_{2}}$
геометрическая свёртка
Рисунок
Название	чередующиеся кубические соты	квадратная мозаика

Решётки A3/D3

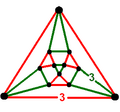
Расположение вершин^[англ.] представляет собой решётку A₃ или решётку D₃^[2][3]. Эта решётка известна в кристаллографии как гранецентрированная кубическая решётка и её называют также кубической решёткой плотной упаковки, поскольку её вершины являются центрами сфер одинакового диаметра в плотной упаковке, которая даёт наивысшую среднюю плотность. Тетраэдрально-октаэдральные соты являются трёхмерным вариантом симлектических сот^[англ.]. Ячейка Вороного этих сот представляет собой ромбододекаэдр, являющийся двойственным телом для кубооктаэдра, вершинной фигурой тетраэдрально-октаэдрльных сот.

Упаковку D+
3 можно построить как объединение двух D₃ (или A₃) решёток. Упаковка D+
n является решёткой только для чётных размерностей. Контактное число равно 2²=4, (2^n-1 для n<8, 240 для n=8 и 2n(n-1) для n>8)^[4].

∪

Решётку A*
3 или D*
3 (то же, что и A4
3 или D4
3) можно построить путём объединения всех четырёх решёток A₃, и она идентична расположению вершин^[англ.] тетрагональных дисфеноидных сот^[англ.], двойственных однородным дважды усечённым кубическим сотам^{[англ.][5]} Решётка является также объёмно-центрированной кубической решёткой, объединением двух кубических сот в двойственном положении.

∪ ∪ ∪ = двойственные для = ∪ .

Контактное число решётки D*
3 равно 8^[6] и её диаграммой Вороного являются дважды усечённые кубические соты^[англ.] , содержащие все усечённые октаэдральные ячейки Вороного ^[7].

Связанные соты

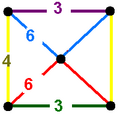
Соты C3

Группа Коксетера [4,3,4], , образует 15 перестановок однородных сот, 9 с различными геометриями, включая чередующиеся кубические соты. Растянутые кубические соты (известные также под названием «обструганные тессерактные соты») геометрически идентичны кубическим сотам.

Соты C3
Кристалло- графическая группа	Фибрифолд[англ.]	Расширенная симметрия[англ.]	Расширенная диаграмма	Порядок	Соты
Pm3m (221)	4−:2	[4,3,4]		×1	1,  2,  3,   4, 5, 6
Fm3m (225)	2−:2	[1+,4,3,4] ↔ [4,31,1]	↔	Половина	7,  11,  12,  13
I43m (217)	4o:2	[[(4,3,4,2+)]]		Половина × 2	(7),
Fd3m (227)	2+:2	[[1+,4,3,4,1+]] ↔ [[3[4]]]	↔	Четверть × 2	10,
Im3m (229)	8o:2	[[4,3,4]]		×2	(1), 8, 9

Соты B3

Группа Коксетера [4,3^1,1], , образует 9 перестановок однородных сот, 4 с различными геометриями, включая чередующиеся кубические соты.

Соты B3
Крист. группа	Фибрифолд[англ.]	Нотация Коксетера[англ.]	Расширенная диаграмма	Порядок	Соты
Fm3m (225)	2−:2	[4,31,1] ↔ [4,3,4,1+]	↔	×1	1, 2, 3, 4
Fm3m (225)	2−:2	<[1+,4,31,1]> ↔ <[3[4]]>	↔	×2	(1), (3)
Pm3m (221)	4−:2	<[4,31,1]>		×2	5, 6, 7, (6), 9, 10, 11

Соты A3

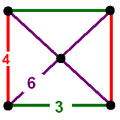
Соты являются одними из пяти различных однородных сот^{[англ.][8]}, построенных на основе группы Коксетера ${\displaystyle {\tilde {A}}_{3}}$. Симметрия может быть умножена на симметрию колец в диаграммах Коксетера — Дынкина:

Соты A3
Крист. группа	Фибрифолд[англ.]	Квадратная симметрия	Нотация Коксетера[англ.]	Расширенная диаграмма	!Расширенная группа	Диаграммы сот
F43m (216)	1o:2	a1	[3[4]]		${\displaystyle {\tilde {A}}_{3}}$	(Нет)
Fm3m (225)	2−:2	d2	<[3[4]]> ↔ [4,31,1]	↔	${\displaystyle {\tilde {A}}_{3}}$×21 ↔ ${\displaystyle {\tilde {B}}_{3}}$	1,  2
Fd3m (227)	2+:2	g2	[[3[4]]] or [2+[3[4]]]	↔	${\displaystyle {\tilde {A}}_{3}}$×22	3
Pm3m (221)	4−:2	d4	<2[3[4]]> ↔ [4,3,4]	↔	${\displaystyle {\tilde {A}}_{3}}$×41 ↔ ${\displaystyle {\tilde {C}}_{3}}$	4
I3 (204)	8−o	r8	[4[3[4]]]+ ↔ [[4,3+,4]]	↔	½${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ½${\displaystyle {\tilde {C}}_{3}}$×2	(*)
Im3m (229)	8o:2		[4[3[4]]] ↔ [[4,3,4]]		${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ${\displaystyle {\tilde {C}}_{3}}$×2	5

Квазиправильные соты

Квазиправильные многогранники и соты: h{4,p,q}

Пространство	Конечное	Аффинное	Компактное	Паракомпактное
Название	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
	${\displaystyle \left\{3,{3 \atop 3}\right\}}$	${\displaystyle \left\{3,{3 \atop 4}\right\}}$	${\displaystyle \left\{3,{3 \atop 5}\right\}}$	${\displaystyle \left\{3,{3 \atop 6}\right\}}$	${\displaystyle \left\{4,{3 \atop 4}\right\}}$	${\displaystyle \left\{4,{4 \atop 4}\right\}}$
Диаграмма Коксетера
Рисунок
Вершинная фигура r{p,3}

Скошенные кубические соты

Скошенные кубические соты
Тип	Выпуклые однородные соты[англ.]
Символ Шлефли	h2{4,3,4}
Диаграммы Коксетера	= =
Ячейки	t{3,4} r{4,3} t{3,3}
Грани	треугольник {3} квадрат {4} шестиугольник {6}
Вершинная фигура	прямоугольная пирамида
Группы Коксетера	[4,31,1], ${\displaystyle {\tilde {B}}_{3}}$ [3[4]], ${\displaystyle {\tilde {A}}_{3}}$
Группа симметрии	Fm3m (225)
Двойственные	сжатые полуоктаэдральные ячейки(en:half oblate octahedrille) Ячейка:
Свойства	вершинно-транзитивная

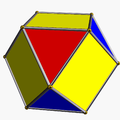
Скошенные кубические соты или усечённые полукубические соты — это однородное заполняющее пространство замощение (или соты) в трёхмерном пространстве. Соты состоят из усечённых октаэдров, кубооктаэдров и усечённых тетраэдров в отношении 1:1:2. Вершинной фигурой сот служит прямоугольная пирамида.

Джон Хортон Конвей назвал эти соты усечёнными тетраэдро-октаэдральными ячейками (en:truncated tetraoctahedrille), а их двойственные сжатыми октаэдральными полуячейками (en:half oblate octahedrille).

 

Симметрия

Соты имеют два различных однородных построения. Построение на основе ${\displaystyle {\tilde {A}}_{3}}$ можно видеть с поочерёдно выкрашенными усечёнными тетраэдрами.

Симметрия	[4,31,1], ${\displaystyle {\tilde {B}}_{3}}$ =<[3[4]]>	[3[4]], ${\displaystyle {\tilde {A}}_{3}}$
Пространственная группа	Fm3m (225)	F43m (216)
Раскраска
Диаграмма Коксетера — Дынкина	=	=
Вершинная фигура

Связанные соты

Соты связаны со скошенными кубическими сотами. Ромбокубооктаэдры уменьшаются до усечённых октаэдров, а кубы уменьшаются до усечённых тетраэдров.

рёберно усечённыt кубические	Скошенные кубические
, , rr{4,3}, r{4,3}, {4,3}	, , t{3,4}, r{4,3}, t{3,3}

Обструганные кубические соты

Обструганные кубические соты
Тип	Выпуклые однородные соты[англ.]
Символ Шлефли	h3{4,3,4}
Диаграммы Коксетера — Дынкина	=
Ячейки	rr{4,3} {4,3} {3,3}
Грани	треугольник {3} квадрат {4}
Вершинная фигура	Усечённая треугольная призма
Группа Коксетера	${\displaystyle {\tilde {B}}_{4}}$, [4,31,1]
Группа симметрии	Fm3m (225)
Двойственные	кубические четвертьячейки?!(en:quarter cubille) Ячейка:
Свойства	вершинно-транзитивные

Струганые кубические соты — это однородные заполняющая пространство мозаика (или соты) в трёхмерном пространстве. Соты состоят из ромбокубооктаэдров, кубов и тетраэдров в отношении 1:1:2. Вершинной фигурой сот служит треугольная призма с тетраэдром на одном конце, кубом на противоположном конце и тремя ромбокубоктаэдрами вокруг трапецеидальных сторон.

Джон Хортон Конвей назвал эти соты 3-RCO-ячейками (en:3-RCO-trille), а двойственные им кубическими четвертьячейками^?! (en:quarter cubille).

Кубические четвертьячейки

Двойственные соты для обструганных кубические сот (en:runcic cubic honeycomb) называются кубическими четвертьячейками (en:quarter cubille) и их диаграммы Коксетера — Дынкина с гранями на 2 из 4 гиперплоскостей фундаментальной области симметрии ${\displaystyle {\tilde {B}}_{4}}$, [4,3^1,1].

Ячейки данных сот можно рассматривать как 1/4 разрезанного куба, которые используют 4 вершины и центр куба. Четыре ячейки находятся вокруг 6 рёбер, а 3 ячейки вокруг 3 рёбер.

Связанные соты

Соты связаны с обструганными кубическими сотами^[англ.]*, у которых четверть кубов альтернировано^[англ.] в тетраэдры, а половина растянута в ромбокубоктаэдры.

Обструганный куб[англ.]*	Обструганные кубические соты =
{4,3}, {4,3}, {4,3}, {4,3} , , ,	h{4,3}, rr{4,3}, {4,3} , ,

---

Двуусечённые кубические соты

Двуусечённые кубические соты
Тип	Выпуклые однородные соты[англ.]
Символ Шлефли	h2,3{4,3,4}
Диаграммы Коксетера	=
Группа Коксетера	${\displaystyle {\tilde {B}}_{4}}$, [4,31,1]
Ячейки	tr{4,3} t{4,3} t{3,3}
Грани	треугольник {3} квадрат {4} шестиугольник {6} octagon {8}
Вершинная фигура
Группа симметрии	Fm3m (225)
Двойственные	половина пирамидальной ячейки?! Ячейка:
Свойства	вершинно-транзитивные

Двуусечённые кубические соты — это заполняющая пространство замощение (или соты) в трёхмерном евклидовом пространстве. Соты состят из усечённых кубооктаэдров, усечённых кубов и усечённых тетраэдров в отношении 1:1:2. Соты связаны со струг-скошеннымы кубическими сотами.

Джон Хортон Конвей назвал эти соты f-tCO-trille, а их двойственные — (половинками пирамидальной ячейки^[англ.], en:half pyramidille).

Половинки пирамидальной ячейки

Двойственные соты для струг-усечённых кубических сот называются половинками пирамидальной ячейки (en:half pyramidille) с диаграммой Коксетера . Грани существуют на 3 из 4 гиперплоскостей группы Коксетера [4,3^1,1], ${\displaystyle {\tilde {B}}_{3}}$.

Ячейки являются неправильными пирамидами и могут рассматриваться как 1/12 куба или 1/24 ромбододекаэдра, каждая из ячеек содержит три угла и центр куба.

Связанные косые бесконечногранники

Существует связанный однородный косой бесконечногранник^[англ.] с тем же расположением вершин^[англ.], но треугольники и квадраты удалены. Его можно рассматривать как расположенные вместе усечённые тетраэдры и усечённые кубы.

Связанные соты

Двуусечённые кубические< соты

струг-скошенные соты

Повёрнутые тетраэдрально-октаэдральные соты

Повёрнутые тетраэдрально-октаэдральные соты
Тип	Выпуклые однородные соты[англ.]
Диаграмм Коксетера
Символ Шлефли	h{4,3,4}:g h{6,3}h{∞} s{3,6}h{∞} s{3[3]}h{∞}
Типы ячеек	{3,3} {3,4}
Грани	треугольники {3}
Вершинная фигура	Трехскатный прямой бикупол G3.4.3.4
Группа	P63/mmc (194) [3,6,2+,∞]
ДвойственныеDual	Трапецеромбические додекаэдральные соты
Свойства	вершинно транзитивные

Повёрнутые тетраэдрально-октаэдральные соты или повёрнутые чередующиеся кубические соты — это заполняющая пространство замощение (или соты) в трёхмерном евклидовом пространстве, состоящие из октаэдров и тетраэдров в отношении 1:2.

Это вершинно-однородная фигура с 8 тетраэдрами и 6 октаэдрами вокруг каждой вершины.

Соты не рёберно-транзитивны. Все рёбра имеют по 2 тетраэдра и 2 октаэдра, но некоторые чередуются, а некоторые соприкасаются.

Эти соты можно рассматривать как зеркальные отражения этих слоёв сот:

Построение с поворотом

Соты являются менее симметричной версией других сот, тетраэдральных-октаэдральных сот, в которых каждое ребро окружено чередующимися тетраэдрами и октаэдрами. Оба вида сот можно рассматривать как слои толщиной в одну ячейку, внутри которых строго чередуются два вида ячеек. Поскольку грани плоскостей, разделяющих эти слои образуют правильную решётку треугольников, смежные слои могут быть размещены так, что каждый октаэдр в одном слое соприкасается с тетраэдром в другом слое, или так, что каждая ячейка соприкасается с ячейкой того же вида (границы слоёв в этом случае становятся плоскостями отражения). Эта последняя форма называется повёрнутой.

Вершинная фигура называется трехскатным прямым бикуполом. Сравните с тетраэдрально-октаэдральными сотами, вершинной фигурой которых служит кубооктаэдр, который (в случае меньшей симметрии) называется треугольным повёрнутым бикуполом.

Вершинные фигуры

Соты	Повёрнутые	Отражённые
Рисунок
Название	трехскатный прямой бикупол	треугольный повёрнутый бикупол
Вершинная фигура
Симметрия	D3h, порядка 12	D3d, порядка 12 (Oh, порядка 48)

Построение путём альтернирования

Вершинная фигура с непланарной конфигурацией вершины 3.3.3.3 для треугольных бипирамид

Геометрия сот может быть получена путём операции альтернирования^[англ.], применённой к шестиугольным призматическим сотам. Ячейки в виде шестиугольных призм становятся октаэдрами, а пустоты создают треугольные бипирамиды, которые можно разбить на пары тетраэдров этих сот. Соты с бипирамилами называются битетраэдральными-октаэдральными сотами. Есть 3 диаграммы Коксетера — Дынкина, которые можно рассмативать как 1, 2 или 3 цвета октаэдров:

1. 
2. 
3. 

Скрученноудлинённые чередующиеся кубические соты

Скрученноудлинённые чередующиеся кубические соты
Тип	Выпуклые однородные соты[англ.]
Символ Шлефли	h{4,3,4}:ge {3,6}h1{∞}
Диаграммы Коксетера
Ячейки	{3,3} {3,4} (3.4.4)
Грани	треугольник {3} квадрат {4}
Вершинная фигура
Пространственная группа	P63/mmc (194) [3,6,2+,∞]
Свойства	вершинно-однородная

Скрученноудлинённые чередующиеся кубические соты — это заполняющее пространство замощение (или соты) в трёхмерном евклидовом пространстве. Соты состоят из октаэдров, треугольных призм и тетраэдров в пропорции 1:2:2.

Соты являются вершинно-однородной фигурой с 3 октаэдрами, 4 тетраэдрами и 6 треугольными призмами вокруг каждой вершины.

Это одни из 28 выпуклых однородных сот^[англ.]

Удлинённые чередующиеся кубические соты^[англ.] имеют то же самое расположение ячеек в каждой вершине но общее расположение отличается. В удлинённой форме каждая призма соприкасается с тетраэдра одной из треугольных граней и октаэдра другой гранью. В скрученноудлинённой форме призма соприкасается одного и того же вида дельтаэдров обоими концами.

Удлинённые чередующиеся кубические соты

Удлинённые чередующиеся кубические соты
Тип	Выпуклые однородные соты[англ.]
Символ Шлефли	h{4,3,4}:e {3,6}g1{∞}
Ячейки	{3,3} {3,4} (3.4.4)
Грани	треугольник {3} квадрат {4}
Вершинная фигура	Трёхскатный купол, соединённый с равнобедренной шестиугольной пирамидой
Группа	[6,(3,2+,∞,2+)] ?
Свойства	вершинно транзитивные

Удлинённые чередующиеся кубические соты — это заполняющее пространство замощение (или соты) в трёхмерном евклидовом пространстве. Соты состоят из октаэдров, треугольных призм и тетраэдров в пропорции 1:2:2.

Соты являются вершинно-однородными с 3 октаэдрами, 4 тетраэдрами и 6 треугольными призмами вокруг каждой вершины. Каждая призма соприкасается с октаэдром одним основанием и с тетраэдром другим.

Это одни из 28 выпуклых однородных сот^[англ.].

Соты имеют повёрнутую форму, которая называется скрученно удлинёнными чередующимися кубическими сотам^[англ.] с тем же расположение ячеек в каждой вершине.

• Кубические соты
• Пространственная конструкция^[англ.]