Сферичний многогранник

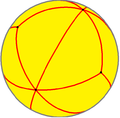
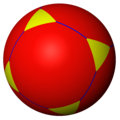
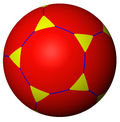
Сферичний многогранник або сферична мозаїка — це мозаїка на сфері, в якій поверхню розділено великими дугами на обмежені ділянки, звані сферичними многокутниками. Значна частина теорії симетричних многогранників використовує сферичні многогранники.

Найвідоміший сферичний многогранник — це футбольний м'яч, який є сферичним зрізаним ікосаедром

Цей пляжний м'яч — приклад осоедра зі шістьма серпоподібними гранями, якщо видалити два білі круги на кінцях.

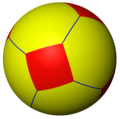
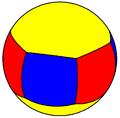
Найвідомішим прикладом сферичного многогранника є футбольний м'яч, який можна розглядати як зрізаний ікосаедр.

Деякі «невласні» многогранники, такі як осоедри та двоїсті їм діедри, існують лише як сферичні многогранники і не мають аналогів із плоскими гранями. У таблиці з прикладами нижче {2, 6} — осоедр, а — {6, 2} двоїстий йому діедр.

Історія

Перші відомі зроблені людиною многогранники — це сферичні многогранники, висічені в камені. Чимало їх знайдено в Шотландії і датовано періодом неоліту.

За часів європейських «темних століть» ісламський учений Абу-ль-Вафа аль-Бузджані написав першу серйозну працю про сферичні многогранники.

На початку XIX століття Пуансо використав сферичні многогранники для виявлення чотирьох правильних зірчастих многогранників.

У середині XX століття Коксетер використав їх для перерахування всіх (за винятком одного) однорідних багатогранників, за допомогою калейдоскопічної побудови (побудова Вітгоффа).

Приклади

Усі правильні, напівправильні многогранники та двоїсті їм можна спроєктувати на сферу як мозаїку. У таблиці нижче наведено символи Шлефлі {p, q} та схеми вершинних фігур a.b.c. …:

Символ Шлефлі	{p, q}	t{p, q}	r{p, q}	t{q, p}	{q, p}	rr{p, q}	tr{p, q}	sr{p, q}
Вершинна фігура	pq	q.2p.2p	p.q.p.q	p. 2q.2q	qp	q.4.p. 4	4.2q.2p	3.3.q.3.p
Тетраедрична симетрія (3 3 2)	33	3.6.6	3.3.3.3	3.6.6	33	3.4.3.4	4.6.6	3.3.3.3.3
		V3.6.6	V3.3.3.3	V3.6.6		V3.4.4.4	V4.6.6	V3.3.3.3.3
Октаедрична симетрія (4 3 2)	43	3.8.8	3.4.3.4	4.6.6	34	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4	V4.6.8[en]	V3.3.3.3.4
Ікосаедрична симетрія (5 3 2)	53	3.10.10	3.5.3.5	5.6.6	35	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.	V4.6.10	V3.3.3.3.5[en]
Діедричні приклади=6 (2 2 6)	62	2.12.12	2.6.2.6	6.4.4	26	4.6.4	4.4.12[en]	3.3.3.6

Клас	2	3	4	5	6	7	8	10
Призма (2 2 p)
Біпіраміда (2 2 p)
Антипризма
Трапецоедр

Невласні випадки

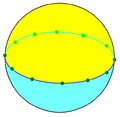
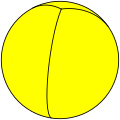
Сферичні мозаїки допускають випадки, які неможливі для многогранників, а саме — осоедри, правильні фігури {2,n}, та діедри, правильні фігури {n,2}.

Сімейство правильних осоедрів

Малюнок
Шлефлі	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}…
Коксетер
Грані та ребра	2	3	4	5	6	7	8
Вершини	2

Правильні діедри: (сферичні мозаїки)

Малюнок
Шлефлі	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}…
Коксетер
Грані	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Ребра та вершини	2	3	4	5	6

Зв'язок із мозаїками на проєктивній площині

Оскільки сфера є дволистим накриттям проєктивної площини, проєктивні многогранники відповідають подвійному накриттю сферичними многогранниками, які мають центральну симетрію.

Найвідомішими прикладами проєктивних многогранників є правильні проєктивні многогранники, утворені з центрально симетричних правильних многогранників, а також із нескінченних сімейств парних діедрів та осоедрів:^[1]

• Напівкуб^[en], {4,3}/2
• Напівоктаедр^[en], {3,4}/2
• Напівдодекаедр, {5,3}/2
• Напівікосаедр, {3,5}/2
• Напівдіедр, {2p,2}/2, p>=1
• Напівосоедр, {2,2p}/2, p>=1

Див. також

• Теселяція
• Сферична геометрія
• Сферична тригонометрія
• Многогранник
• Проєктивний многогранник^[en]
• Тороїдальний многогранник