Сферический многогранник

Сферический многогранник или сферическая мозаика — это тa мозаика на сфере, в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.

Наиболее известный сферический многогранник — это футбольный мяч, рассматриваемый как сферический усечённый икосаэдр.

Этот пляжный мяч^[англ.] показывает осоэдр с шестью серповидными гранями, если удалить два белых круга на концах.

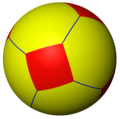
Наиболее известным примером сферического многогранника служит футбольный мяч, который можно понимать как усечённый икосаэдр.

Некоторые «несобственные» многогранники, такие как осоэдры и их двойственные диэдры, существуют только как сферические многогранники и не имеют аналогов с плоскими гранями. В таблице с примерами ниже {2, 6} — осоэдр, а — {6, 2} двойственный ему диэдр.

История

Первые известные сделанные человеком многогранники — это сферические многогранники, высеченные в камне. Многие из них были найдены в Шотландии и датируются периодом Неолита.

Во времена европейских «тёмных столетий» исламский учёный Абуль-Вафа аль-Бузджани написал первую серьёзную работу о сферических многогранниках.

Две сотни лет назад, в начале 19-го века, Пуансо использовал сферические многогранники для обнаружения четырёх правильных звёздчатых многогранников.

В середине 20-го века Коксетер использовал их для перечисления всех (за исключением одного) однородных многогранников, посредством калейдоскопического построения (Построение Витхоффа).

Примеры

Все правильные, полуправильные многогранники и их двойственные можно спроектировать на сферу как мозаику. В таблице ниже указаны символы Шлефли {p, q} и схема вершинной фигуры a.b.c. …:

Символ Шлефли	{p, q}	t{p, q}	r{p, q}	t{q, p}	{q, p}	rr{p, q}	tr{p, q}	sr{p, q}
Вершинная фигура	pq	q.2p.2p	p.q.p.q	p. 2q.2q	qp	q.4.p. 4	4.2q.2p	3.3.q.3.p
Тетраэдральные (3 3 2)	33	3.6.6	3.3.3.3	3.6.6	33	3.4.3.4	4.6.6	3.3.3.3.3
		V3.6.6	V3.3.3.3	V3.6.6		V3.4.4.4	V4.6.6	V3.3.3.3.3
Октаэдральные (4 3 2)	43	3.8.8	3.4.3.4	4.6.6	34	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4	V4.6.8[англ.]	V3.3.3.3.4
Икосаэдральные (5 3 2)	53	3.10.10	3.5.3.5	5.6.6	35	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.4	V4.6.10	V3.3.3.3.5[англ.]
Диэдральные примеры=6 (2 2 6)	62	2.12.12	2.6.2.6	6.4.4	26	4.6.4	4.4.12[англ.]	3.3.3.6

Класс	2	3	4	5	6	7	8	10
Призма (2 2 p)
Бипирамида (2 2 p)
Антипризма
Трапецоэдр

Несобственные случаи

Сферические мозаики допускают случаи, которые невозможны для многогранников, а именно — осоэдры, правильные фигуры {2,n}, и диэдры, правильные фигуры {n,2}.

Семейство правильных осоэдров

Рисунок
Шлефли	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}…
Коксетер
Грани и рёбра	2	3	4	5	6	7	8
Вершины	2

Правильные диэдры: (сферические мозаики)

Рисунок
Шлефли	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}…
Коксетер
Грани	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Рёбра и вершины	2	3	4	5	6

Связь с мозаиками на проективной плоскости

Поскольку сфера является двулистным накрытием проективной плоскости, проективные многогранники соответствуют двойному накрытию сферическими многогранниками, имеющими центральную симметрию.

Наиболее известными примерами проективных многогранников служат правильные проективные многогранники, образованные из центрально симметричных правильных многогранников, а также из бесконечных семейств чётных диэдров и осоэдров: ^[1]

• Полукуб^[англ.], {4,3}/2
• Полуоктаэдр^[англ.], {3,4}/2
• Полудодекаэдркуб^[англ.], {5,3}/2
• Полуикосаэдр, {3,5}/2
• Полудиэдр, {2p,2}/2, p>=1
• Полуосоэдр, {2,2p}/2, p>=1

См. также

• Мозаика
• Сферическая геометрия
• Сферическая тригонометрия
• Многогранник
• Проективный многогранник^[англ.]
• Тороидальный многогранник
• Нотация Конвея для многогранников