Призма (геометрия)

У этого термина существуют и другие значения, см. Призма.

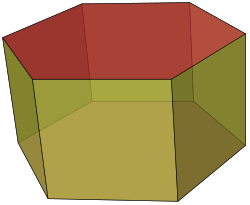
При́зма (${\displaystyle n}$-угольная) (лат. prisma от др.-греч. πρίσμα «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками (${\displaystyle n}$-угольниками), лежащими в параллельных плоскостях, а остальные ${\displaystyle n}$ граней — параллелограммы, имеющие общие стороны с этими многоугольниками.

Множество однородных призм
Шестиугольная призма
Тип	Однородный многогранник
Свойства	вершинно транзитивный выпуклый многогранник
Комбинаторика
Элементы	3n ребра 2n вершины
Грани	Всего - 2+n 2{n} n {4}
Конфигурация вершины	4.4.n
Двойственный многогранник	Бипирамида
Развёртка
Классификация
Символ Шлефли	{n}×{} or t{2, n}
Диаграмма Дынкина
Группа симметрии	Dnh?!, [n,2], (*n22), порядок 4n
Медиафайлы на Викискладе

Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.

Многоугольник, лежащий в основании, определяет название призмы: треугольник — треугольная призма, четырёхугольник — четырёхугольная; пятиугольник — пятиугольная (пентапризма) и т. д.

Призма является частным случаем цилиндра в общем смысле (некругового).

Элементы призмы

Название	Определение	Обозначения на чертеже	Чертеж
Основания	Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных друг другу плоскостях.	${\displaystyle ABCDE}$, ${\displaystyle KLMNP}$
Боковые грани	Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом.	${\displaystyle ABLK}$, ${\displaystyle BCML}$, ${\displaystyle CDNM}$, ${\displaystyle DEPN}$, ${\displaystyle EAKP}$
Боковая поверхность	Поверхность всех граней по кругу, но без оснований.
Полная поверхность	Поверхность обоих оснований и всех граней боковой поверхности.
Боковые рёбра	Общие стороны боковых граней.	${\displaystyle AK}$, ${\displaystyle BL}$, ${\displaystyle CM}$, ${\displaystyle DN}$, ${\displaystyle EP}$
Высота	Отрезок, соединяющий плоскости, в которых лежат основания призмы и перпендикулярный этим плоскостям.	${\displaystyle KR}$
Диагональ	Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.	${\displaystyle BP}$
Диагональная плоскость	Плоскость, проходящая через боковое ребро призмы и диагональ основания.	${\displaystyle EBP}$
Диагональное сечение	Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат.	${\displaystyle EBLP}$
Перпендикулярное (ортогональное) сечение	Пересечение призмы и плоскости, перпендикулярной её боковому ребру.

Свойства призмы

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые рёбра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

${\displaystyle V=S\cdot h}$

• Объём призмы с правильным n-угольным основанием равен

${\displaystyle V={\frac {n}{4}}hs^{2}\mathrm {ctg} {\frac {\pi }{n}}}$ (здесь s — длина стороны многоугольника).

• Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
• Площадь боковой поверхности произвольной призмы ${\displaystyle S=P\cdot l}$, где ${\displaystyle P}$ — периметр перпендикулярного сечения, ${\displaystyle l}$ — длина бокового ребра.
• Площадь боковой поверхности прямой призмы ${\displaystyle S=P\cdot h}$, где ${\displaystyle P}$ — периметр основания призмы, ${\displaystyle h}$ — высота призмы.
• Площадь боковой поверхности прямой призмы с правильным ${\displaystyle n}$-угольным основанием равна

${\displaystyle A={\frac {n}{2}}s^{2}\mathrm {ctg} {\frac {\pi }{n}}+nsh.}$

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное сечение перпендикулярно ко всем боковым граням.
• Двойственным многогранником прямой призмы является бипирамида.

Виды призм

Призма, основанием которой является параллелограмм, называется параллелепипедом.

Прямая призма — это призма, у которой боковые рёбра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками^[1].

Прямая прямоугольная призма называется также прямоугольным параллелепипедом. Символ Шлефли такой призмы — { }×{ }×{ }.

Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.

Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником. Символ Шлефли такой призмы — t{2,p}.

Усечённая треугольная призма

Прямые призмы с правильными основаниями и одинаковыми длинами рёбер образуют одну из двух бесконечных последовательностей полуправильных многогранников (другую последовательность образуют антипризмы).

Наклонными называются призмы, рёбра которых не перпендикулярны плоскости основания.

Усечённая призма — многогранник, который отсекается от призмы непараллельной основанию плоскостью^[2]. Усечённая призма сама призмой не является.

Диаграммы Шлегеля

Основная статья: Диаграмма Шлегеля

Треугольная призма

4-угольная призма

5-угольная призма

6-угольная призма

7-угольная призма

8-угольная призма

Симметрия

Группой симметрии прямой ${\displaystyle n}$-угольной призмы с правильным основанием является группа D_nh порядка 4n, за исключением куба, который имеет группу симметрии O_h^[англ.] порядка 48, содержащую три версии D_4h в качестве подгрупп. Группой вращений^[англ.] является D_n порядка 2n, за исключением случая куба, для которого группой вращений является группа O^[англ.] порядка 24, имеющая три версии D₄ в качестве подгрупп.

Группа симметрии D_nh включает центральную симметрию в том и только в том случае, когда n чётно.

Обобщения

Призматические многогранники

Призматический многогранник — это обобщение призмы в пространствах размерности 4 и выше. ${\displaystyle n}$-мерный призматический многогранник конструируется из двух (n − 1)-мерных многогранников, перенесённых в следующую размерность.

Элементы призматического n-мерного многогранника удваиваются из элементов (n − 1)-мерного многогранника, затем создаются новые элементы следующего уровня.

Возьмём ${\displaystyle n}$-мерный многогранник с элементами ${\displaystyle f_{i}}$ (i-мерная грань, i = 0, …, n). Призматический (${\displaystyle n+1}$)-мерный многогранник будет иметь ${\displaystyle 2f_{i}+f_{-1}}$ элементов размерности i (при ${\displaystyle f_{-1}=0}$, ${\displaystyle f_{n}=1}$).

По размерностям:

• Берём многоугольник с ${\displaystyle n}$ вершинами и ${\displaystyle n}$ сторонами. Получим призму с 2${\displaystyle n}$ вершинами, 3${\displaystyle n}$ рёбрами и ${\displaystyle 2+n}$ гранями.
• Берём многогранник с v вершинами, e рёбрами и f гранями. Получаем (4-мерную) призму с 2v вершинами, ${\displaystyle 2e+v}$ рёбрами, ${\displaystyle 2f+e}$ гранями и ${\displaystyle 2+f}$ ячейками.
• Берём 4-мерный многогранник с v вершинами, e рёбрами, f гранями и c ячейками. Получаем (5-мерную) призму с 2v вершинами, ${\displaystyle 2e+v}$ рёбрами, ${\displaystyle 2f+e}$ (2-мерными) гранями, ${\displaystyle 2c+f}$ ячейками и ${\displaystyle 2+c}$ гиперячейками.

Однородные призматические многогранники

Правильный ${\displaystyle n}$-многогранник, представленный символом Шлефли {p, q, ..., t}, может образовать однородный призматический многогранник размерности (n + 1), представленный прямым произведением двух символов Шлефли: {p, q, ..., t}×{}.

По размерностям:

• Призма из 0-мерного многогранника — это отрезок, представленный пустым символом Шлефли {}.
  • 
• Призма из 1-мерного многогранника — это прямоугольник, полученный из двух отрезков. Эта призма представляется как произведение символов Шлефли {}×{}. Если призма является квадратом, запись можно сократить: {}×{} = {4}.
  • Пример: Квадрат, {}×{}, два параллельных отрезка, соединённые двумя другими отрезками, сторонами.
• многоугольная призма — это 3-мерная призма, полученная из двух многоугольников (один получен параллельным переносом другого), которые связаны прямоугольниками. Из правильного многоугольника {p} можно получить однородную n-угольную призму, представленную произведением {p}×{}. Если p = 4, призма становится кубом: {4}×{} = {4, 3}.
  • Пример: Пятиугольная призма, {5}×{}, два параллельных пятиугольника связаны пятью прямоугольными сторонами.
• 4-мерная призма, полученная из двух многогранников (один получен параллельным переносом другого), со связывающими 3-мерными призматическими ячейками. Из правильного многогранника {p, q} можно получить однородную 4-мерную призму, представленную произведением {p, q}×{}. Если многогранник является кубом и стороны призмы тоже кубы, призма превращается в тессеракт: {4, 3}×{} = {4, 3, 3}.
  • Пример: додекаэдральная призма^[англ.], {5, 3}×{}, два параллельных додекаэдра, соединённых 12 пятиугольными призмами (сторонами).
• …

Призматические многогранники более высоких размерностей также существуют как прямые произведения двух любых многогранников. Размерность призматического многогранника равна произведению размерностей элементов произведения. Первый пример такого произведения существует в 4-мерном пространстве и называется дуопризмами, которые получаются произведением двух многоугольников. Правильные дуопризмы представляются символом {p}×{q}.

Семейство правильных призм

Многоугольник
Мозаика
Конфигурация	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	17.4.4	∞.4.4

Скрученная призма и антипризма

Скрученная призма — это невыпуклый призматический многогранник, полученный из однородной q-угольной путём деления боковых граней диагональю и вращения верхнего основания, обычно на угол ${\displaystyle {\frac {\pi }{q}}}$ радиан (${\displaystyle {\frac {180}{q}}}$ градусов), в направлении, при котором стороны становятся вогнутыми^[3][4].

Скрученная призма не может быть разбита на тетраэдры без введения новых вершин. Простейший пример с треугольными основаниями называется многогранником Шёнхардта.

Скрученная призма топологически идентична антипризме, но имеет половину симметрий: D_n, [n,2]⁺, порядка 2n. Эту призму можно рассматривать как выпуклую антипризму, у которой удалены тетраэдры между парами треугольников.

Треугольная	Четырёхугольные		12-угольная
Многогранник Шёнхардта	Скрученная квадратная антипризма	Квадратная антипризма	Скрученная двенадцатиугольная антипризма

Связанные многогранники и мозаики

Семейство правильных призм

Многоугольник
Мозаика
Конфигурация	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	17.4.4	∞.4.4

Семейство выпуклых куполов

n	2	3	4	5	6
Название	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}
Купол	Диагональный купол	Трёхскатный купол	Четырёхскатный купол	Пятискатный купол	Шестискатный купол (плоский)
Связанные однородные многогранники	Треугольная призма	Кубооктаэдр	Ромбокубо- октаэдр	Ромбоикосо- додекаэдр	Ромботри- шестиугольная мозаика[англ.]

Симметрии

Призмы топологически являются частью последовательности однородных усечённых многогранников с конфигурациями вершин (3.2n.2n) и [n,3].

Варианты симметрии *n32 усечённых мозаик: 3.2n.2n
Симметрия *n32 [n,3]	Сферическая				Евклидова	Компактная гиперболич.		Параком- пактная	Некомпактная гиперболич.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Усечённые фигуры
Конфигурация	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12[англ.]	3.14.14[англ.]	3.16.16[англ.]	3.∞.∞[англ.]	3.24i.24i	3.18i.18i	3.12i.12i
Разделённые фигуры
Конфигурация	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12[англ.]	V3.14.14[англ.]	V3.16.16	V3.∞.∞

Призмы топологически являются частью последовательности скошенных многогранников с вершинными фигурами (3.4.n.4) и мозаик на гиперболической плоскости. Эти вершинно транзитивные фигуры имеют (*n32) зеркальную симметрию^[англ.].

Варианты симметрии *n42 расширенных мозаик: 3.4.n.4
Симметрия *n32 [n,3]	Сферическая				Евклидова	Компактная гиперболическая		Паракомпактная
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Фигура
Конфигурация	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4[англ.]	3.4.7.4[англ.]	3.4.8.4[англ.]	3.4.∞.4[англ.]

Соединение многогранников

Существует 4 однородных соединения треугольных призм:

Соединение четырёх треугольных призм^[англ.], соединение восьми треугольных призм^[англ.], соединение десяти треугольных призм^[англ.], соединение двенадцати треугольных призм^[англ.].

Соты

Существует 9 однородных сот, включающих ячейки в виде треугольных призм:

• гироудлинённые альтернированные кубические соты^[англ.],
• удлинённые альтернированные кубические соты^[англ.],
• повёрнутые треугольные призматические соты,
• плосконосые квадратные призматические соты^[англ.],
• треугольные призматические соты,
• треугольно-шестиугольные призматические соты,
• усечённые шестиугольные призматические соты,
• ромботришестиугольные призматические соты,
• плосконосые шестиугольные призматические соты,
• удлинённые треугольные призматические соты.

Связанные многогранники

Треугольная призма является первым многогранником в ряду полуправильных многогранников^[англ.]. Каждый последующий однородный многогранник содержит в качестве вершинной фигуры предыдущий многогранник. Торольд Госсет^[англ.] идентифицировал эту серию в 1900 как содержащую все фасеты правильных многомерных многогранников, все симплексы и ортоплексы (правильные треугольники и квадраты для случая треугольных призм). В нотации Коксетера треугольная призма задаётся символом −1₂₁.

k21[англ.] в пространстве размерности n
Пространство	Конечное						Евклидово	Гиперболическое
En[англ.]	3	4	5	6	7	8	9	10
Группа Коксетера	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇[англ.]	E₈	E₉ = Ẽ₈ = E₈+	E₁₀ = T₈ = E₈++
Диаграмма Коксетера
Симметрия[англ.]	[3−1,2,1]	[30,2,1]	[31,2,1]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Порядок	12	120	192	51 840	2 903 040	696 729 600	∞
Граф							-	-
Обозначение	−121	021	121	221[англ.]	321[англ.]	421[англ.]	521[англ.]	621[англ.]

Четырёхмерное пространство

Треугольная призма служит ячейкой во множестве четырёхмерных однородных 4-мерных многогранников^[англ.], включая:

тетраэдральная призма[англ.]	октаэдральная призма[англ.]	кубооктаэдральная призма[англ.]	икосаэдральная призма[англ.]	икосододекаэдральная призма[англ.]	усечённая додекаэдральная призма[англ.]
ромбоикоси- додекаэдральная призма[англ.]	ромбокуб- октаэдральная призма[англ.]	усечённая кубическая призма[англ.]	плосконосая додекаэдральная призма[англ.]	n-угольная антипризматическая призма[англ.]
скошенный 5-ячейник[англ.]	скошено-усечённый 5-ячейник[англ.]	обструганный 5-ячейник[англ.]	струг-усечённый 5-ячейник[англ.]	скошенный тессеракт[англ.]	скошено-усечённый тессеракт[англ.]	обструганный тессеракт[англ.]	струг-усечённый тессеракт[англ.]
скошенный 24-ячейник[англ.]	скошено-усечённый 24-ячейник[англ.]	обструганный 24-ячейник[англ.]	струг-усечённый 24-ячейник[англ.]	скошенный 120-ячейник[англ.]	скошено-усечённый 120-ячейник[англ.]	обструганный 120-ячейник[англ.]	струг-усечённый 120-ячейник[англ.]

См. также

• Антипризма
• Параллелограмм
• Параллелепипед