Трисхилий купол

У геометрії трисхилий купол — призматоїд, що складається з правильного шестикутника (нижня основа купола), правильного трикутника (верхня грань, що паралельна основі), та бічних граней: 3 прямокутників та 3 рівнобедрених трикутників.

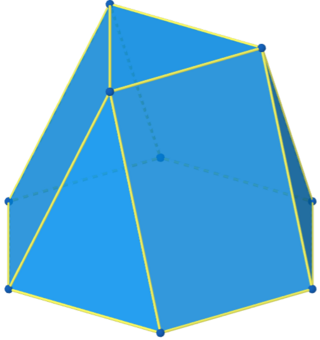
Належить до родини куполів і є підкласом призматоїдів.

Два куполи можуть бути з'єднані по їх нижній основі, утворюючи багатогранник бікупол^[en], в прямій (якщо з'єднані однойменні грані) або повернутій (якщо з'єднані різнойменні грані) орієнтації.

Багатогранник Джонсона J3

Трисхилий купол
Тип	Багатогранник Джонсона J3 Призматоїд, множина куполів.
Властивості	Опуклий, рівносторонній, правильногранний
Комбінаторика
Елементи	8 граней ((3+1){3} + 3{4} + 1{6}) 15 ребер 9 вершин: 6 вершин (3-го степеня) + 3(4-го)
Грані	3+1 Правильних трикутників, 3 Квадрата, 1 Правильний шестикутник.
Характеристика Ейлера	${\displaystyle \chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2}$
Конфігурація вершини	6(3.4.6) 3(3.4.3.4)
Вершинна фігура	3 прямокутника з довжинами сторін 1 та ${\displaystyle {\sqrt {2}}}$ 6 трикутників з довжинами сторін 1, ${\displaystyle {\sqrt {2}}}$, ${\displaystyle {\sqrt {3}}}$
Класифікація
Позначення	• J3 (в нотації Нормана Джонсона[en]) • M4 (в нотації Залгаллера[1]) • U3 = Q3 [2] (в нотації Конвея[en]) • Q3 (в нотації Стюарта)
Символ Шлефлі	{3} || t{3}
Група симетрії	C3v[en], [3], (*33), порядок 6 (Циклічна симетрія 3-Піраміди)
Група поворотів	C3, [3]+, (33), порядок 3
Двоїстий багатогранник	Напіврозсічений трикутний трапецоедр
Розгортка

Рівносторонній трисхилий купол є одним із багатогранників Джонсона (J₃ або M₄ (за Залгаллером^[1]).

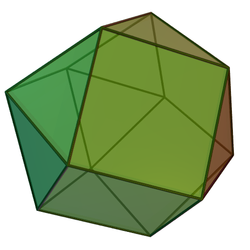
Трисхилий купол можна розглядати як половину кубооктаедра.

Багатогранник Джонсона — один із 92 строго опуклих багатогранників, що мають правильні грані, але не є однорідним (тобто він не є правильним багатогранником, архімедовим тілом, призмою або антипризмою). Правильногранні багатогранники названі ім'ям Нормана Джонсона^[en], який першим перелічив їх в 1966 р. ^[2]

Трисхилий купол складено з 8 граней: 3+1 = 4 правильних трикутників, 3 квадратів та 1 правильного шестикутника.

Одна трикутна грань оточена трьома квадратами; три трикутних граней оточені двома квадратними та однією шестикутною гранню; квадратні грані оточені трьома трикутними та однією шестикутною гранями; шестикутна грань оточена трьома трикутними та трьома квадратними гранями^{[джерело?]}.

Має 15 ребер однакової довжини: 3+6 = 9 ребер розташовані між квадратною та трикутною гранями, 3 ребра — між трикутною та шестикутною гранями, решта 3 — між квадратною та шестикутною гранями.

У трисхилого купола 9 вершин: 3 вершини оточені двома трикутними та двома квадратними гранями (почергово); 6 вершин оточені трикутною, квадратною та шестикутною гранями.

Трисхилий купол може бути отриманий шляхом поділу навпіл кубооктаедра по шестикутному перерізу між двома протилежними трикутними гранями.

Навпаки, два трисхилих куполи можна поєднати у поверненій орієнтації по шестикутній грані, і отримати кубооктаедр.

Трисхилий купол має вісь поворотної симертії 3-го порядку, що проходить через центри основ; а також три площини дзеркальної симетрії, що проходять через вісь купола та середини сторін нижньої основи^{[джерело?]}.

Формули

Діагоналі

Кількість діагоналей опуклого багатогранника: ${\displaystyle {\binom {B}{2}}-P}$ , де В — кількість вершин, Р — кількість ребер багатогранника. Для трисхилого купола:

${\displaystyle {\binom {9}{2}}-15={\frac {9}{2}}\cdot {\frac {8}{1}}-15=21}$ діагоналі (15 граневих та 6 просторових).

Діагоналі трисхилого купола з довжиною ребра ${\displaystyle a}$
	Граневі діагоналі	${\displaystyle AB={\sqrt {2}}\cdot a\approx 1.41421356237\cdot a}$ ${\displaystyle AC={\sqrt {3}}\cdot a\approx 1.73205080756\cdot a}$ ${\displaystyle AD=2\cdot a}$
	Просторові діагоналі	${\displaystyle FC={\sqrt {3}}\cdot a\approx 1.73205080756\cdot a}$

Метричні характеристики

Описана сфера трисхилого купола

Середньовписана сфера трисхилого купола

Для трисхилого купола з довжиною ребра ${\displaystyle a}$:
Радіус описаної сфери (проходить через всі вершини)		${\displaystyle R=a}$
Радіус напіввписаної сфери (дотикається до всіх ребер)		${\displaystyle \rho ={\frac {\sqrt {3}}{2}}\cdot a}$	${\displaystyle \approx 0.8660254\cdot a}$
Вписаної сфери трисхилий купол не має
Висота H (Відстань між паралельними трикутною та шестикутною гранями)		${\displaystyle H={\frac {\sqrt {6}}{3}}\cdot a}$	${\displaystyle \approx 0.81649658\cdot a}$
Площа поверхні		${\displaystyle S=\left(3+{\frac {5{\sqrt {3}}}{2}}\right)\cdot a^{2}}$	${\displaystyle \approx 7.33012701\cdot a^{2}}$
Об'єм		${\displaystyle V={\frac {5}{6}}{\sqrt {2}}\cdot a^{3}}$	${\displaystyle \approx 1.1785113\cdot a^{3}}$

Кути

Плоскі кути граней при вершині: 60°, 90°, 120°.

Кути багатогранника
Кут між несусідніми ребрами при вершині верхньої основи	${\displaystyle \varphi =\arccos \left(-{\frac {1}{2}}\right)}$	${\displaystyle ={\frac {2\pi }{3}}}$ rad = 120°
Двогранний кут між гранями {3} та {4}	${\displaystyle \alpha =\arccos \left(-{\frac {\sqrt {3}}{3}}\right)=\operatorname {arcsec} \left(-{\sqrt {3}}\right)}$	≈ 2.1862760354 rad ≈ 125°15′ 51.8028′′
Двогранний кут між гранями {3} та {6}	${\displaystyle \beta =\arccos \left({\frac {1}{3}}\right)=\operatorname {arcsec} \left(3\right)}$	≈ 1.2309594173 rad ≈ 70° 31′ 43.60571′′
Двогранний кут між гранями {4} та {6}	${\displaystyle \gamma =\arccos \left({\frac {\sqrt {3}}{3}}\right)=\operatorname {arcsec} \left({\sqrt {3}}\right)}$	≈ 0.9553166181 rad ≈ 54°44′ 8.197142′′
Тілесний кут при вершині нижньої основи (шестикутної)	${\displaystyle \Omega _{1}={\frac {1}{2}}\arccos \left(-{\frac {7}{9}}\right)=2\arcsin \left({\frac {\sqrt {3}}{3}}\right)=}$ ${\displaystyle =4\arctan \left({\sqrt {3}}-{\sqrt {2}}\right)}$	${\displaystyle \Omega \thickapprox 1.2309594}$ ср
Тілесний кут при вершині верхньої основи (трикутної)	${\displaystyle \Omega _{2}=\arccos \left(-{\frac {7}{9}}\right)=4\arcsin \left({\frac {\sqrt {3}}{3}}\right)=}$ ${\displaystyle =8\arctan \left({\sqrt {3}}-{\sqrt {2}}\right)}$	${\displaystyle \Omega _{2}\thickapprox 2.4619188}$ ср
Сферичність	${\displaystyle \Psi ={\frac {2{\sqrt[{3}]{50\pi }}}{6+5{\sqrt {3}}}}}$	${\displaystyle \Psi \thickapprox 0.7360858}$

Центр тяжіння трисхилого купола лежить на його осі симетрії на відстані ${\displaystyle {\frac {\sqrt {6}}{8}}\cdot a}$ від нижньої основи^[3].

Двоїстий багатогранник

Трисхилий купол не має ні топологічно-двоїстого багатогранника (вершини двоїстого знаходяться в центрах граней вихідного багатогранника), ні канонічно-двоїстого багатогранника (середньовписані сфери обох багатогранників збігаються).

Його двоїстий може бути побудований лише загальним чином (кожній грані вихідного багатогранника відповідає вершина двоїстого, кожній вершині вихідного — грань дуального, з дотриманням симетрії вихідного багатогранника), а тому форми та розміри двоїстого багатогранника до вихідного трисхилого купола можуть різнитися.

Двоїстий до трисхилого купола має 9 граней: 6 трикутників + 3 дельтоїда; 15 ребер, 8 вершин^[4][5].

Обертання двоїстого до трисхилого купола багатогранника

Двоїстий багатогранник	Розгортка двоїстого

Споріднені багатогранники

Трисхилий купол належить до родини куполів. Сімейство n-куполів з правильними гранями існує до n = 5 включно.

Сімейство опуклих куполів

n	2	3	4	5	6	7
Назва	Двосхилий купол	Трисхилий купол	Чотирисхилий купол	П'ятисхилий купол	Шестисхилий купол (плоский)	Семисхилий купол (з неправильними бічними гранями)
Символ Шлефлі	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}	{7} || t{7}
Купол
Пов'язані однорідні багатогранники	Трикутна призма	Кубооктаедр	Ромбокубо- октаедр	Ромбоікосо- додекаедр	Ромботри- шестикутна мозаїка[en]	Ромботри- семикутна мозаїка[en]

Два трисхилих куполи можуть бути з'єднані своїми шестикутними основами в прямій орієнтації (поєднуються однойменні бокові грані); отриманий багатогранник — триcхилий прямий бікупол^[en] (J₂₇). Якщо один з куполів повернути на 60º, то отримаємо триcхилий повернутий бікупол, більш відомий як [[Кубооктаедр|кубоктаедр^{[джерело?]}]].

Трисхилий прямий бікупол	Трисхилий повернутий бікупол (кубооктаедр)

Нарощений трисхилий купол, майже-багатогранник Джонсона з компланарними гранями

Трисхилий купол можна наростити трьома квадратними пірамідами, залишаючи суміжні копланарні грані без змін. Отриманий багатогранник, нарощений трисхилий купол, належить до родини майже багатогранників Джонсона^[en] з компланарними гранями.

Якщо об'єднати ці копланарні трикутники в єдині грані, отримаємо топологічно ще один трисхилий купол, бічні грані якого є рівнобедреними трапеціями. Якщо всі трикутні грані зберегти без змін, а шестикутник в основі розбити на 6 трикутників, вийде копланарний дельтаедр з 22 гранями^{[джерело?]}.