Wykres funkcji

Wykres funkcji – dwuznaczne pojęcie matematyczne:

• dla dowolnych zbiorów ${\displaystyle X,\ Y}$ i funkcji między nimi ${\displaystyle (f:X\to Y)}$ jej wykresem nazywa się zbiór par uporządkowanych dany wzorem^[2]:

${\displaystyle S_{f}=\left\{{\big (}x,\;f(x){\big )}:x\in X\right\};}$

innymi słowy wykres tworzą pary złożone z argumentu i odpowiedniej wartości;

• wykres funkcji to także przedstawienie jej graficznie, prezentując powyższy zbiór lub jego część^[3]. Jest to możliwe tylko dla niektórych funkcji, o odpowiedniej dziedzinie i przeciwdziedzinie, m.in. dla przypadków opisanych niżej.

Przykład krzywej Gaussa – wykresu rozkładu normalnego w kartezjańskim układzie współrzędnych^[1]. Szara siatka przedstawia pewną własność takich wykresów, opisaną niżej

Teoria grawitacji Newtona opisuje potencjał grawitacyjny jako funkcję rzeczywistą czterech zmiennych rzeczywistych – trzech współrzędnych przestrzennych oraz jednej czasowej. Dla ustalonej chwili i płaszczyzny liczba zmiennych (argumentów) tej funkcji spada do dwóch. Tutaj przedstawiono wykres potencjału grawitacyjnego w pobliżu Ziemi i Księżyca – użyto poziomic, zaznaczonych na czerwono. Są też znane jako linie ekwipotencjalne

Sens mnogościowy

Rzeczywiste argumenty i wartości

W pierwszym wypadku argumenty funkcji i jej wartości mogą być między innymi liczbami rzeczywistymi. W szczególności – jeśli ${\displaystyle X,\ Y\subseteq \mathbb {R} ,}$ to funkcja ${\displaystyle f:X\to Y}$ jest nazywana funkcją rzeczywistą jednej zmiennej rzeczywistej. Jej wykresem są wszystkie punkty postaci ${\displaystyle (x,y),}$ gdzie ${\displaystyle x\in X}$ oraz ${\displaystyle y=f(x)\in Y.}$ Jest to podzbiór płaszczyzny kartezjańskiej, którą da się utożsamić z płaszczyzną euklidesową. Wzajemną odpowiedniość (bijekcję) zapewnia tu dowolny układ współrzędnych kartezjańskich^[4][5].

Argumenty funkcji i jej wartości mogą też należeć do innych zbiorów, np. wielowymiarowych przestrzeni kartezjańskich. Zbiór wszystkich par ${\displaystyle \{(x,y):x\in X,y\in Y\}}$ oznacza się ${\displaystyle X\times Y}$ i nazywa się iloczynem kartezjańskim. Jeśli ${\displaystyle D\subseteq X\times Y\subseteq \mathbb {R} ^{2},}$ to dowolną funkcję ${\displaystyle f:D\to Z}$ nazywa się funkcją dwóch zmiennych rzeczywistych. Jeśli ${\displaystyle Z\subseteq \mathbb {R} ,}$ to wykresem funkcji rzeczywistej ${\displaystyle f}$ są wtedy wszystkie punkty postaci^[6]:

${\displaystyle {\big (}x,\;y,\;f(x,\;y){\big )}\in D\times \mathbb {R} \subseteq \mathbb {R} ^{3}.}$

Taka funkcja to inaczej pole skalarne na płaszczyźnie kartezjańskiej lub jej fragmencie. Funkcje tego typu można przedstawiać na co najmniej trzy sposoby – figurami dwu- lub trójwymiarowymi, co pokazują ilustracje obok.

W ogólności, gdy ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} ^{m},}$ ${\displaystyle n,m\in \mathbb {N} _{+},}$ to:

${\displaystyle S_{f}=\left\{{\big (}x,\;f(x){\big )}:x\in \mathbb {R} ^{n}\right\}\subseteq \mathbb {R} ^{n+m}.}$

Przypadek ogólny

Wykresy rozumiane w ten sposób – jako podzbiory odpowiednich iloczynów kartezjańskich – to jednoznaczne relacje dwuczłonowe między dziedziną funkcji a przeciwdziedziną swojej funkcji. Takie pojęcie wykresu pokrywa się z jedną z formalnych definicji samej funkcji – definicją Peana^[7].

Sens graficzny

Wykresy przykładowych funkcji rzeczywistycj o dwóch zmiennych rzeczywistych. Są to wykresy w kartezjańskim układzie współrzędnych o trzech wymiarach. Ciągłość tych funkcji sprawia, że ich wykresy są powierzchniamil; te konkretne należą do rodziny nazywanej kwadrykami

Wykres potencjału elektrycznego dla elektrycznego dipolu. Taki potencjał to inny przykład funkcji rzeczywistej o dwóch zmiennych rzeczywistych ${\displaystyle (\mathbb {R} ^{2}\supseteq X}$${\displaystyle \to }$${\displaystyle Y\subseteq \mathbb {R} ).}$ Na tym wykresie połączono obie metody prezentacji takich funkcji – jest powierzchnia zawieszona w trójwymiarze, ale są też izolinie

Informacje ogólne

Jak wspomniano wyżej, wykresy rozumiane graficznie są możliwe tylko dla niektórych funkcji, o odpowiednich dziedzinach i przeciwdziedzinach. Jeśli ${\displaystyle f:X\to Y,}$ to wykres jest możliwy m.in. dla funkcji:

• rzeczywistych jednej zmiennej rzeczywistej: ${\displaystyle X,\ Y\subseteq \mathbb {R}$ ;}
• rzeczywistych dwóch zmiennych rzeczywistych: ${\displaystyle X\subseteq \mathbb {R} ^{2},\ Y\subseteq \mathbb {R}$ ;}
• zespolonych jednej zmiennej rzeczywistej: ${\displaystyle X\subseteq \mathbb {R} ,\ Y\subseteq \mathbb {C}$ ;}
• zespolonych jednej zmiennej zespolonej: ${\displaystyle X,\ Y\subseteq \mathbb {C} .}$

Funkcje rzeczywiste jednej zmiennej rzeczywistej

Wykresy takich funkcji najczęściej są przedstawiane w kartezjańskim układzie współrzędnych^[3]. Jednoznaczność funkcji jest związana z pewną własnością geometryczną takiego wykresu. Każda prosta pionowa – tj. równoległa do osi wartości – przecina taki wykres co najwyżej raz^[8][9]. Widać to na jednej z ilustracji – niebieski wykres rozkładu normalnego jest przecinany przez szare, pionowe linie i każda z nich przecina wykres dokładnie raz.

Wykres takiej funkcji nie musi być krzywą – może:

• być układem rozłącznych krzywych – por. wykresy funkcji signum, podłogi i sufitu;
• w ogóle nie zawierać krzywych – por. wykresy funkcji Dirichleta i funkcji Riemanna.

Z takiego wykresu da się odczytać podstawowe własności funkcji:

• dziedzina funkcji – ta część osi argumentów, która jest nad wykresem, pod nim lub się z nim pokrywa; dziedzina funkcji to rzut prostokątny wykresu na oś argumentów;
• miejsca zerowe – przecięcia wykresu z osią argumentów;
• punkty ekstremalne;
• punkty osobliwe;
• monotoniczność;
• okresowość.

Funkcje rzeczywiste dwóch zmiennych rzeczywistych

Niech dziedzina funkcji będzie obszarem na płaszczyźnie euklidesowej. Jeśli ta funkcja jest ciągła, to jej wykres jest powierzchnią^[6]; przykłady podano na ilustracjach. Powierzchnia wykresu może być „zawieszona” nad tym obszarem, pod nim lub go przecinać.

Funkcje zespolone

Wykres funkcji dzeta (ζ) Riemanna obciętej (zawężonej) do prostej krytycznej. Jest to wykres kartezjański dwóch funkcji rzeczywistych – części rzeczywistej (Re ζ) i części urojonej (Im ζ)

Inny wykres tej samej funkcji, także w kartezjańskim układzie współrzędnych. Zastosowano tu inną technikę – równania obu funkcji to równania parametryczne pokazanej krzywej płaskiej

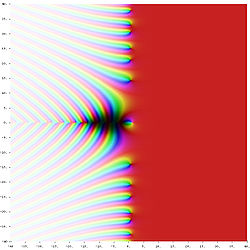
Wykres funkcji dzeta (ζ) dla różnych argumentów, także tych spoza prostej krytycznej. Zastosowano tu kolorowanie dziedziny

Zobacz też

• wykres