均匀多面体对偶

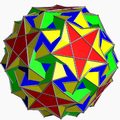
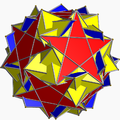
均匀多面体对偶或称均匀对偶、对偶均匀多面体（Dual uniform polyhedron）是均匀多面体的对偶多面体。^[1] 均匀多面体是一种点可递的立体，由于对偶的特性，因此均匀多面体对偶皆为面可递的立体。^[2]均匀多面体对偶可以利用多曼·卢克构造从均匀多面体构造。^[3]

均匀多面体对偶

部分的均匀多面体对偶 菱形十二面体 （卡塔兰立体） 大菱形三十面体 五方偏方面体 （偏方面体） 正八面体 （柏拉图立体） 双四角锥 （双锥体）

种类

均匀多面体对偶是均匀多面体的对偶多面体，因此每一个均匀多面体都有一个对应的均匀多面体对偶。^[1]

• 5个柏拉图立体（凸正多面体）。除了正四面体是自身对偶多面体外，其余四个立体两两一组互为对偶（立方体与正八面体、正十二面体与正二十面体）
• 4个开普勒－庞索立体（星形正多面体）。四个立体两两一组互为对偶（小星形十二面体与大十二面体、大星形十二面体与大二十面体）
• 13个凸卡塔兰立体。这些立体是属于均匀多面体的阿基米德立体之对偶多面体。^[4]
• 53个星形均匀多面体的对偶多面体。^[1][5]
• 所有的双锥体。双锥体是属于均匀多面体的棱柱体之对偶多面体。^[6]
• 所有的偏方面体。偏方面体是属于均匀多面体的反棱柱之对偶多面体。^[7]

温尼尔（英语：Magnus J. Wenninger）在其著作《对偶模型》（Dual Models）描述了所有的均匀多面体对偶以及建构其模型的说明。

多曼·卢克构造

均匀多面体的对偶多面体可以使用多曼·卢克构造（Dorman Luke construction）来构造。其构造的方法为：对偶多面体的每个面通过使用多曼·卢克构造的方法从原始多面体对应的顶点图导出。^[9][10]

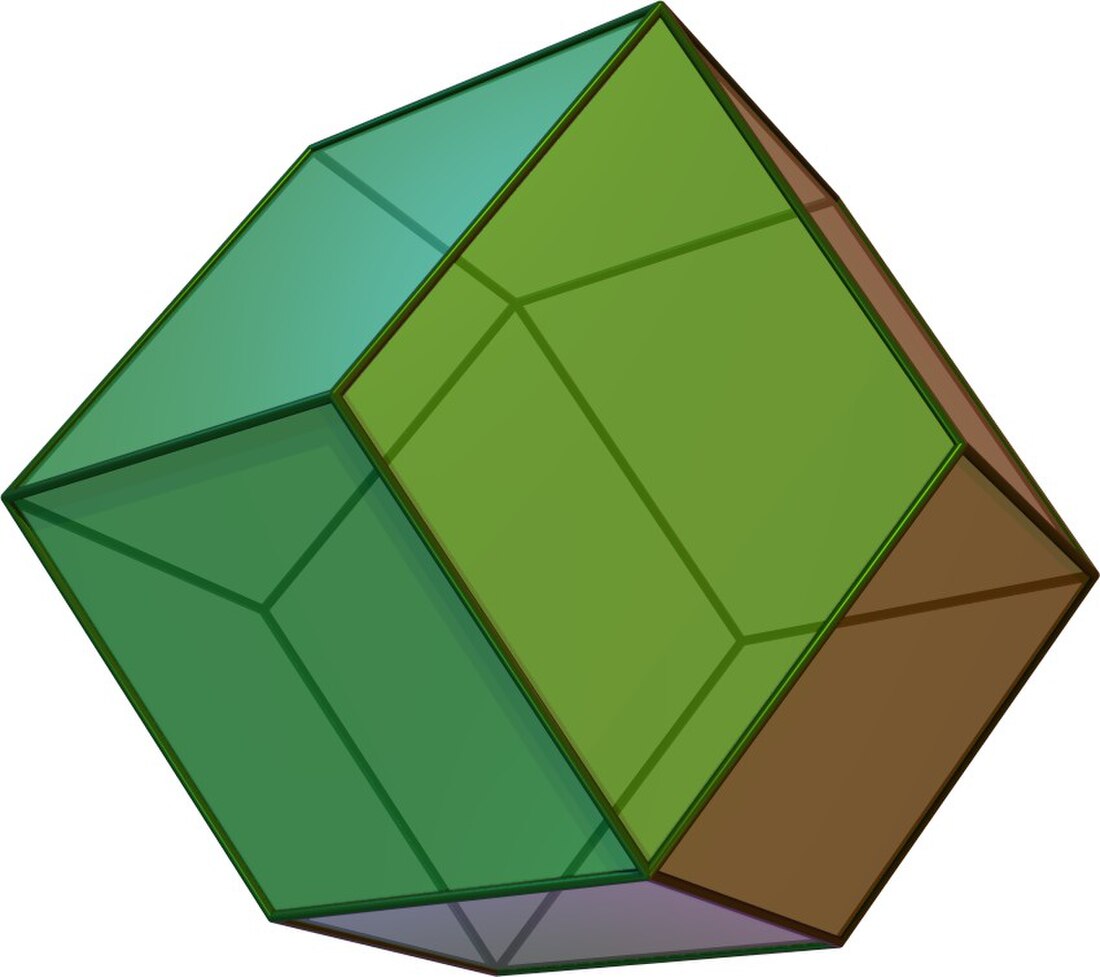
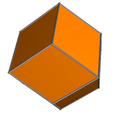
举例来说，截半立方体的对偶多面体是菱形十二面体^[11]。要从截半立方体构造其对偶多面体时，其顶点图（在下图以红色显示）可以用来导出对偶多面体菱形十二面体的对应面（在下图以蓝色显示）。

多曼·卢克构造的具体步骤如下：

1. 在任一顶角周围上选择点A、B、C、D，并令这四个点与顶角的顶点V满足VA = VB = VC = VD。（此例使用中点）
2. 绘制其顶点图ABCD。
3. 绘制ABCD的外接圆。
4. 分别作过A、B、C、D与ABCD的外接圆相切的切线。
5. 将切线两两相交的交点标记为E、F、G、H

线段EF、FG、GH、HE已绘制为切线的一部分。多边形EFGH即为原始顶点V对应在对偶多面体上的面。

此例选择的顶点图的大小恰好让其外接圆位于截半立方体的中分球上，而截半立方体的中分球同时也成为以此构造方式构造出的菱形十二面体之中分球。多曼·卢克构造只有在存在中分球的多面体上才能使用。^[12]例如，均匀多面体一般都存在中分球，因此可以应用于均匀多面体对偶的构造上。

列表

名称	图像	种类	面数	边数	顶点数	对称性	对偶多面体
正四面体		柏拉图立体	4	6	4	Td, A3, [3,3], (*332)	正四面体 （自身对偶）
立方体		柏拉图立体	6	12	8	Oh, B3, [4,3], (*432)	正八面体
正八面体		柏拉图立体	8	12	6	Oh, BC3, [4,3], (*432)	立方体
正十二面体		柏拉图立体	12	30	20	Ih, H3, [5,3], (*532)	正二十面体
正二十面体		柏拉图立体	20	30	12	Ih, H3, [5,3], (*532)	正十二面体
小星形十二面体		开普勒－庞索立体	12	30	12	Ih（英语：Icosahedral symmetry）, H3, [5,3], (*532)	大十二面体
大十二面体		开普勒－庞索立体	12	30	12	Ih（英语：Icosahedral symmetry）, H3, [5,3], (*532)	小星形十二面体
大星形十二面体		开普勒－庞索立体	12	30	20	Ih（英语：Icosahedral symmetry）, H3, [5,3], (*532)	大二十面体
大二十面体		开普勒－庞索立体	20	30	12	Ih（英语：Icosahedral symmetry）, H3, [5,3], (*532)	大星形十二面体
三角化四面体		卡塔兰立体	12	18	8	Td, A3, [3,3], *332	截角四面体
菱形十二面体		卡塔兰立体	12	24	14	Oh, B3, [4,3], (*432)	截半立方体
三角化八面体		卡塔兰立体	24	36	14	Oh, B3, [4,3], (*432)	截角立方体
四角化立方体		卡塔兰立体	24	36	14	Oh, B3, [4,3], (*432)	截角八面体
鸢形二十四面体		卡塔兰立体	24	48	26	Oh, BC3, [4,3], (*432)	小斜方截半立方体
四角化菱形十二面体		卡塔兰立体	48	72	26	Oh, B3, [4,3], (*432)	大斜方截半立方体
五角二十四面体		卡塔兰立体	24	60	38	Oh, ½BC3, [4,3], (*432)	扭棱立方体
菱形三十面体		卡塔兰立体	30	60	32	Ih, H3, [5,3], (*532)	截半二十面体
三角化二十面体		卡塔兰立体	60	90	32	Ih, H3, [5,3], (*532)	截角十二面体
五角化十二面体		卡塔兰立体	60	90	32	Ih, H3, [5,3], (*532)	截角二十面体
鸢形六十面体		卡塔兰立体	60	120	62	Ih, H3, [5,3], (*532)	小斜方截半二十面体
四角化菱形三十面体		卡塔兰立体	120	180	62	Ih, H3, [5,3], (*532)	大斜方截半二十面体
五角六十面体		卡塔兰立体	60	150	92	Ih, H3, [5,3], (*532)	扭棱十二面体
四面半无穷星形六面体		无穷星形多面体	6	12	7	Td, [3,3], (*332)	四面半六面体
立方半无穷星形八面体		无穷星形多面体	12	24	10	Oh, [4,3], (*432)	立方半八面体
立方半无穷星形八面体		无穷星形多面体	12	24	12	Oh, [4,3], (*432)	八面半八面体
反平行四边形二十四面体		星形多面体	24	48	18	Oh, [4,3], (*432)	大斜方立方体
大六角二十四面体		星形多面体	24	48	20	Oh, [4,3], (*432)	大立方截半立方体
大鸢形二十四面体		星形多面体	24	48	26	Oh, [4,3], (*432)	非凸大斜方截半立方体
小反平行四边形二十四面体		星形多面体	24	48	18	Oh, [4,3], (*432)	小斜方立方体
小六角星化二十四面体（英语：Small hexacronic icositetrahedron）		星形多面体	24	48	20	Oh, [4,3], (*432)	小立方立方八面体
大三角化八面体		星形多面体	24	36	14	Oh, [4,3], (*432)	星形截角立方体
大六角化八面体（英语：Great disdyakis dodecahedron）		星形多面体	48	72	26	Oh, [4,3], (*432)	星形截角截半立方体
四重二方六面体（维基数据：Q18048480）		星形多面体	48	72	20	Oh, [4,3], (*432)	立方截角立方八面体
小星形五角化十二面体		星形多面体	60	90	24	Ih, [5,3], (*532)	截角大十二面体
大十二角星化六十面体（英语：Great dodecacronic hexecontahedron）		星形多面体	60	120	44	Ih, [5,3], (*532)	大十二面截半二十面体
大凧形六十面体（英语：Great deltoidal hexecontahedron）		星形多面体	60	120	62	Ih, [5,3], (*532)	非凸大斜方截半二十面体
大菱形十二面六十面体（英语：Great rhombidodecacron）		星形多面体	60	120	42	Ih, [5,3], (*532)	大斜方十二面体
中鸢形六十面体（英语：Medial deltoidal hexecontahedron）		星形多面体	60	120	54	Ih, [5,3], (*532)	斜方截半大十二面体
内侧二十角星化六十面体（英语：Medial icosacronic hexecontahedron）		星形多面体	60	120	44	Ih, [5,3], (*532)	二十面化截半大十二面体
斜方星形二十面体		星形多面体	60	120	50	Ih, [5,3], (*532)	斜方二十面体
小六角六十面体（英语：Small hexagonal hexecontahedron）		星形多面体	60	180	112	Ih, [5,3], (*532)	完全扭棱二十面体
小二十面半无穷星形十二面体（英语：Small icosihemidodecacron）		无穷星形多面体	30	60	26	Ih, [5,3], (*532)	小二十面半十二面体
小十二面半无穷星形十二面体（英语：Small dodecahemidodecacron）		无穷星形多面体	30	60	18	Ih, [5,3], (*532)	小十二面半十二面体
大菱形三十面体		星形多面体	30	60	32	Ih, [5,3], (*532)	大截半二十面体
大十二面半无穷星形十二面体（英语：Great dodecahemidodecacron）		无穷星形多面体	30	60	18	Ih, [5,3], (*532)	大十二面半十二面体
大二十面半无穷星形十二面体（英语：Great icosihemidodecacron）		无穷星形多面体	30	60	26	Ih, [5,3], (*532)	大二十面半十二面体
内侧菱形三十面体		星形多面体	30	60	24	Ih, [5,3], (*532)	截半大十二面体
小十二面半无穷星形二十面体（英语：Small dodecahemicosacron）		无穷星形多面体	30	60	22	Ih, [5,3], (*532)	小十二面半二十面体
大十二面半无穷星形二十面体（英语：Great dodecahemicosacron）		无穷星形多面体	30	60	22	Ih, [5,3], (*532)	大十二面半二十面体
大双三角十二角星化六十面体（英语：Great ditrigonal dodecacronic hexecontahedron）		星形多面体	60	120	44	Ih, [5,3], (*532)	大双三角十二面截半二十面体
大二十角星化六十面体（英语：Great icosacronic hexecontahedron）		星形多面体	60	120	52	Ih, [5,3], (*532)	大二十面化截半二十面体
大十二面二十面六十面体		星形多面体	60	120	32	Ih, [5,3], (*532)	大十二面二十面体
小六角星六十面体（英语：Small hexagrammic hexecontahedron）		星形多面体	60	180	112	Ih, [5,3], (*532)	小反屈扭棱二十面截半二十面体
小三角六边形二十面体		星形多面体	20	60	32	Ih, [5,3], (*532)	小双三斜三十二面体
内侧三角六边形二十面体		星形多面体	20	60	24	Ih, [5,3], (*532)	双三斜十二面体
大三角六边形二十面体		星形多面体	20	60	32	Ih, [5,3], (*532)	大双三斜三十二面体
小十二角星化六十面体（维基数据：Q18048505）		星形多面体	60	120	44	Ih, [5,3], (*532)	小十二面截半二十面体
小星形菱形十二面体（英语：Small rhombidodecacron）		星形多面体	60	120	42	Ih, [5,3], (*532)	小斜方十二面体
大五角化十二面体		星形多面体	60	90	24	Ih, [5,3], (*532)	小星形截角十二面体
大星形五角化十二面体		星形多面体	60	90	32	Ih, [5,3], (*532)	截角大二十面体
小二十角星化六十面体（英语：Small icosacronic hexecontahedron）		星形多面体	60	120	52	Ih, [5,3], (*532)	小二十面化截半二十面体
小双三角十二角星化六十面体（英语：Small ditrigonal dodecacronic hexecontahedron）		星形多面体	60	120	44	Ih, [5,3], (*532)	小双三角十二面截半二十面体
小十二面二十面六十面体（英语：Small dodecicosacron）		星形多面体	60	120	32	Ih, [5,3], (*532)	小十二面二十面体
大三角化二十面体（英语：Great triakis icosahedron）		星形多面体	60	90	32	Ih, [5,3], (*532)	大星形截角十二面体
大二重斜方截半二十面无穷星形六十面体（英语：Great dirhombicosidodecacron）		无穷星形多面体	60	240	124	Ih, [5,3], (*532)	大二重斜方截半二十面体
大六角六十面体（英语：Great hexagonal hexecontahedron）		星形多面体	60	180	104	Ih, [5,3], (*532)	大扭棱十二面截半二十面体
大二重扭棱二重斜方十二面无穷星形六十面体（维基数据：Q18048492）		无穷星形多面体	60	360	204	Ih, [5,3], (*532)	大二重扭棱二重斜方十二面体
三重二方二十面体（英语：Tridyakis icosahedron）		星形多面体	120	180	44	Ih, [5,3], (*532)	二十面截角十二面十二面体
内侧双二方三十面体（英语：Medial disdyakis triacontahedron）		星形多面体	120	180	54	Ih, [5,3], (*532)	截角截半大十二面体
大四角化菱形三十面体（维基数据：Q18048490）		星形多面体	120	180	62	Ih, [5,3], (*532)	大截角截半二十面体
中五角六十面体（英语：Medial pentagonal hexecontahedron）		星形多面体	60	150	84	Ih, [5,3], (*532)	扭棱小星形十二面体
中六角六十面体（英语：Medial hexagonal hexecontahedron）		星形多面体	60	180	104	Ih, [5,3], (*532)	扭棱二十面化截半大十二面体
大五角六十面体（英语：Great pentagonal hexecontahedron）		星形多面体	60	150	92	Ih, [5,3], (*532)	扭棱大星形十二面体
大逆五角六十面体（维基数据：Q18048506）		星形多面体	60	150	92	Ih, [5,3], (*532)	反扭棱大星形十二面体
中逆五角六十面体（英语：Medial inverted pentagonal hexecontahedron）		星形多面体	60	150	84	Ih, [5,3], (*532)	反扭棱小星形十二面体
大五角星六十面体（英语：Great pentagrammic hexecontahedron）		星形多面体	60	150	92	Ih, [5,3], (*532)	大反屈扭棱截半二十面体

参见

• 均匀多面体