Portal:Mathematics
Wikipedia portal for content related to Mathematics / From Wikipedia, the free encyclopedia
Portal maintenance status: (December 2018)
|
The Mathematics Portal
Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)
Featured articles – load new batch
- Image 1

The weighing pans of this balance scale contain zero objects, divided into two equal groups.
In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": it is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...) - Image 2The number π (/paɪ/; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number π appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such asare commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found.
For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of π for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated π to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for π, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...) - Image 3One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)
Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...) - Image 4

Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.
In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...) - Image 5
Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor, German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...) - Image 6
Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...) - Image 7

The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.
In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:(Full article...) - Image 8

Plots of logarithm functions, with three commonly used bases. The special points logb b = 1 are indicated by dotted lines, and all curves intersect in logb 1 = 0.
In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm baseof 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x. When the base is clear from the context or is irrelevant it is sometimes written log x.
The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is frequently used in computer science. (Full article...) - Image 9

Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).
In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...) - Image 10
The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...) - Image 11

Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...) - Image 12
Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...) - Image 13In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...) - Image 14

The manipulations of the Rubik's Cube form the Rubik's Cube group.
In mathematics, a group is a set with an operation that satisfies the following constraints: the operation is associative and has an identity element, and every element of the set has an inverse element. The set is closed under the operation.
Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called (these properties characterize the integers in a unique way). (Full article...) - Image 15
Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Selected image – show another
Good articles – load new batch
- Image 1

The mutilated chessboard
The mutilated chessboard problem is a tiling puzzle posed by Max Black in 1946 that asks:Suppose a standard 8×8 chessboard (or checkerboard) has two diagonally opposite corners removed, leaving 62 squares. Is it possible to place 31 dominoes of size 2×1 so as to cover all of these squares?
(Full article...) - Image 2
Two greedy colorings of the same crown graph using different vertex orders. The right example generalises to 2-colorable graphs with n vertices, where the greedy algorithm expends n/2 colors.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
Different choices of the sequence of vertices will typically produce different colorings of the given graph, so much of the study of greedy colorings has concerned how to find a good ordering. There always exists an ordering that produces an optimal coloring, but although such orderings can be found for many special classes of graphs, they are hard to find in general. Commonly used strategies for vertex ordering involve placing higher-degree vertices earlier than lower-degree vertices, or choosing vertices with fewer available colors in preference to vertices that are less constrained. (Full article...) - Image 3

An antiparallelogram
In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, each pair of sides is antiparallel with respect to the other, with sides in the longer pair crossing each other as in a scissors mechanism. Whereas a parallelogram's opposite angles are equal and oriented the same way, an antiparallelogram's are equal but oppositely oriented. Antiparallelograms are also called contraparallelograms or crossed parallelograms.
Antiparallelograms occur as the vertex figures of certain nonconvex uniform polyhedra. In the theory of four-bar linkages, the linkages with the form of an antiparallelogram are also called butterfly linkages or bow-tie linkages, and are used in the design of non-circular gears. In celestial mechanics, they occur in certain families of solutions to the 4-body problem. (Full article...) - Image 4

Three of the ordinary lines in a 4 × 4 grid of points
The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.
A line that contains exactly two of a set of points is known as an ordinary line. Another way of stating the theorem is that every finite set of points that is not collinear has an ordinary line. According to a strengthening of the theorem, every finite point set (not all on one line) has at least a linear number of ordinary lines. An algorithm can find an ordinary line in a set ofpoints in time. (Full article...) - Image 5
Sir Isaac Newton FRS (25 December 1642 – 20 March 1726/27) was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author who was described in his time as a natural philosopher. He was a key figure in the Scientific Revolution and the Enlightenment that followed. His pioneering book Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687, consolidated many previous results and established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating infinitesimal calculus, though he developed calculus years before Leibniz.
In the Principia, Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. He used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for tides, the trajectories of comets, the precession of the equinoxes and other phenomena, eradicating doubt about the Solar System's heliocentricity. He demonstrated that the motion of objects on Earth and celestial bodies could be accounted for by the same principles. Newton's inference that the Earth is an oblate spheroid was later confirmed by the geodetic measurements of Maupertuis, La Condamine, and others, convincing most European scientists of the superiority of Newtonian mechanics over earlier systems. (Full article...) - Image 6

16 polygonalizations of a set of six points
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
Every point set that does not lie on a single line has at least one polygonalization, which can be found in polynomial time. For points in convex position, there is only one, but for some other point sets there can be exponentially many. Finding an optimal polygonalization under several natural optimization criteria is a hard problem, including as a special case the travelling salesman problem. The complexity of counting all polygonalizations remains unknown. (Full article...) - Image 7
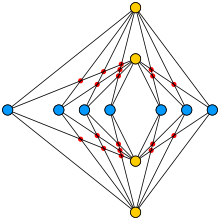
An optimal drawing of K4,7, with 18 crossings (red dots)
In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of a complete bipartite graph. The problem is named after Pál Turán, who formulated it while being forced to work in a brick factory during World War II.
A drawing method found by Kazimierz Zarankiewicz has been conjectured to give the correct answer for every complete bipartite graph, and the statement that this is true has come to be known as the Zarankiewicz crossing number conjecture. The conjecture remains open, with only some special cases solved. (Full article...) - Image 8
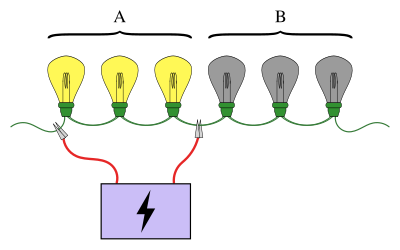
An illustration of the lightbulb problem, where one is searching for a broken bulb among six lightbulbs. Here, the first three are connected to a power supply, and they light up (A). This indicates that the broken bulb must be one of the last three (B). If instead the bulbs did not light up, one could be sure that the broken bulb was among the first three. Continuing this procedure can locate the broken bulb in no more than three tests, compared to a maximum of six tests if the bulbs are checked individually.
In statistics and combinatorial mathematics, group testing is any procedure that breaks up the task of identifying certain objects into tests on groups of items, rather than on individual ones. First studied by Robert Dorfman in 1943, group testing is a relatively new field of applied mathematics that can be applied to a wide range of practical applications and is an active area of research today.
A familiar example of group testing involves a string of light bulbs connected in series, where exactly one of the bulbs is known to be broken. The objective is to find the broken bulb using the smallest number of tests (where a test is when some of the bulbs are connected to a power supply). A simple approach is to test each bulb individually. However, when there are a large number of bulbs it would be much more efficient to pool the bulbs into groups. For example, by connecting the first half of the bulbs at once, it can be determined which half the broken bulb is in, ruling out half of the bulbs in just one test. (Full article...) - Image 9

Title page of De quinque corporibus regularibus
De quinque corporibus regularibus (sometimes called Libellus de quinque corporibus regularibus) is a book on the geometry of polyhedra written in the 1480s or early 1490s by Italian painter and mathematician Piero della Francesca. It is a manuscript, in the Latin language; its title means [the little book] on the five regular solids. It is one of three books known to have been written by della Francesca.
Along with the Platonic solids, De quinque corporibus regularibus includes descriptions of five of the thirteen Archimedean solids, and of several other irregular polyhedra coming from architectural applications. It was the first of what would become many books connecting mathematics to art through the construction and perspective drawing of polyhedra, including Luca Pacioli's 1509 Divina proportione (which incorporated without credit an Italian translation of della Francesca's work). (Full article...) - Image 10In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex. Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex. (Full article...)
- Image 11

YBC 7289
YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest known computational accuracy ... in the ancient world". The tablet is believed to be the work of a student in southern Mesopotamia from some time between 1800 and 1600 BC. (Full article...) - Image 12In geometry, the Beckman–Quarles theorem states that if a transformation of the Euclidean plane or a higher-dimensional Euclidean space preserves unit distances, then it preserves all Euclidean distances. Equivalently, every homomorphism from the unit distance graph of the plane to itself must be an isometry of the plane. The theorem is named after Frank S. Beckman and Donald A. Quarles Jr., who published this result in 1953; it was later rediscovered by other authors and re-proved in multiple ways. Analogous theorems for rational subsets of Euclidean spaces, or for non-Euclidean geometry, are also known. (Full article...)
Did you know (auto-generated) – load new batch

- ... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?
- ... that the prologue to The Polymath was written by Martin Kemp, a leading expert on Leonardo da Vinci?
- ... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
- ... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
- ... that mathematician Mathias Metternich was one of the founders of the Jacobin club of the Republic of Mainz?
- ... that the mathematical infinity symbol ∞ may be derived from the Roman numerals for 1000 or for 100 million?
- ... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
- ... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
More did you know – view different entries

- ...that it is impossible to trisect a general angle using only a ruler and a compass?
- ...that in a group of 23 people, there is a more than 50% chance that two people share a birthday?
- ...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
- ...the hyperbolic trigonometric functions of the natural logarithm can be represented by rational algebraic fractions?
- ... that economists blame market failures on non-convexity?
- ... that, according to the pizza theorem, a circular pizza that is sliced off-center into eight equal-angled wedges can still be divided equally between two people?
- ... that the clique problem of programming a computer to find complete subgraphs in an undirected graph was first studied as a way to find groups of people who all know each other in social networks?
































