Łączność (matematyka)

Łączność, asocjatywność^[1] – własność niektórych działań dwuargumentowych zdefiniowana odpowiednią równością, podaną niżej. Łączność dotyczy:

• części działań arytmetycznych jak dodawanie liczb rzeczywistych i ich mnożenie^[1];
• niektórych działań, które bywają nauczane w szkołach średnich, np. pewnych działań na zbiorach, wektorach i funkcjach, w tym ciągach;
• części działań z matematyki wyższej, np. łączność zdarza się dla działań na liczbach zespolonych, hiperzespolonych, macierzach i ogólnych relacjach dwuargumentowych.

Ilustracja łączności dodawania liczb rzeczywistych na osi liczbowej: ${\displaystyle (x+y)+z=x+(y+z)}$ dla dowolnych ${\displaystyle x,y,z\in \mathbb {R} }$

Łączność dodawania i mnożenia to twierdzenia nauczane w polskich szkołach podstawowych, umieszczone w podstawie programowej kursów matematyki^[2]. Łączność ma też znaczenie w matematyce bardziej zaawansowanej – jako:

• własność innych działań, wspomnianych wyżej;
• cecha definiująca istotne struktury w algebrze abstrakcyjnej.

Nazwę łączności wprowadził William Rowan Hamilton w I połowie XIX wieku^[3].

Definicje

Diagram przedstawiający łączność działania

Niech ${\displaystyle X}$ oznacza dowolny zbiór, a kwadrat ${\displaystyle \diamond }$ – działanie dwuargumentowe w tym zbiorze: ${\displaystyle \diamond :X^{2}\to X.}$ Działanie to nazywa się łącznym, jeśli dla wszystkich trójek elementów ${\displaystyle a,b,c\in X}$ zachodzi równość^[1]:

${\displaystyle a\diamond (b\diamond c)=(a\diamond b)\diamond c.}$

Łączność oznacza, że jeśli układ nawiasów jest sensowny – czyli zgodny ze składnią – to nie wpływa na wynik. Można więc najpierw wykonać działanie wskazane przez dowolny z dwóch operatorów ${\displaystyle \diamond ,}$ a potem wykonać działanie wskazane przez drugi z nich. Dlatego jeśli istotny jest tylko wynik obliczeń, a nie ich dokładny przebieg, to można zapisywać to działanie bez nawiasów:

${\displaystyle a\diamond b\diamond c.}$

Działanie, które nie jest łączne, nazywa się niełącznym^[4][5]. Uwaga – łączność działań dwuargumentowych:

• bywa zapisywana inaczej, przez inny zapis działań, opisany w jednej z dalszych sekcji;
• ma też bardziej zaawansowaną definicję, podaną w innej dalszej sekcji.

Przykłady łączności

Dodawanie wektorów na płaszczyźnie jest łączne: ${\displaystyle ({\vec {a}}+{\vec {b}})+{\vec {c}}={\vec {a}}+({\vec {b}}+{\vec {c}})}$

Arytmetyka i algebra

• Dodawanie liczb rzeczywistych^[1], zespolonych^[6] oraz kwaternionów^[7][8];
• mnożenie powyższych obiektów^[1][6][7][8]:

${\displaystyle {\begin{aligned}a,b,c&\in \mathbb {H} \Rightarrow \\(ab)c&=a(bc);\end{aligned}}}$

• dodawanie macierzy o ustalonych wymiarach^[9][a]:

${\displaystyle {\begin{aligned}&n,m\in \mathbb {N} _{+},\ A,B,C\in M_{n\times m}\Rightarrow \\&(A+B)+C=A+(B+C);\end{aligned}}}$

• mnożenie macierzy kwadratowych^[9][b]:

${\displaystyle {\begin{aligned}A,B,C&\in M_{n\times n}\Rightarrow \\(AB)C&=A(BC).\end{aligned}}}$

Podstawy matematyki

Diagram Venna przedstawiający łączność sumy zbiorów^[10]: ${\displaystyle (A\cup B)\cup C=}$${\displaystyle A\cup (B\cup C)}$

Diagram Venna przedstawiający łączność przekroju zbiorów^[11]: ${\displaystyle (A\cap B)\cap C=}$${\displaystyle A\cap (B\cap C)}$

Diagram Venna przedstawiający łączność różnicy symetrycznej zbiorów^[12]: ${\displaystyle (A{\dot {-}}B){\dot {-}}C=}$${\displaystyle A{\dot {-}}(B{\dot {-}}C)}$

• Suma zbiorów^[10] ${\displaystyle (A\cup B),}$ przekrój zbiorów^[11] ${\displaystyle (A\cap B)}$ i ich różnica symetryczna^[12] ${\displaystyle (A{\dot {-}}B);}$
• rzut pary uporządkowanej na lewy element^[13]:

${\displaystyle {\begin{aligned}\pi _{1}:(a;b)\mapsto \ &a\Rightarrow \\(a\pi _{1}b)\pi _{1}c=\ &a=a\pi _{1}(b\pi _{1}c);\end{aligned}}}$

• konkatenacja skończonych ciągów, zwanych też krotkami^[14];
• złożenie funkcji^[15]:

${\displaystyle (f\circ g)\circ h=f\circ (g\circ h);}$

• złożenie relacji dwuargumentowych^[16][17];

${\displaystyle (R\circ S)\circ T=R\circ (S\circ T).}$

Analiza matematyczna

• splot funkcji^[18]:

${\displaystyle \left(f_{1}*f_{2}\right)*f_{3}=f_{1}*\left(f_{2}*f_{3}\right).}$

Przykłady niełączności

Najczęściej stosowana jest notacja z lewostronną łącznością (np. niełączne działania arytmetyczne), co wiąże się z powszechną praktyką zapisywania (i odczytywania) od lewej tekstu lub wyrażeń arytmetycznych, z kolejnością wprowadzania od lewej wyrażeń do kalkulatorów itd.

Działania lewostronnie łączne

• odejmowanie jest niełączne; np.

${\displaystyle 1-(1-1)\neq (1-1)-1;}$

dla odejmowania stosuje się domyślnie notację lewostronnie łączną, tj.

${\displaystyle 1-1-1=(1-1)-1=-1;}$

• dzielenie jest niełączne; np.

${\displaystyle 2:(2:2)\neq (2:2):2;}$

dla dzielenia stosuje się domyślnie notację lewostronnie łączną, tj.

${\displaystyle 2:2:2=(2:2):2=0,5.}$

Działania prawostronnie łączne

• potęgowanie jest niełączne^[1]; np.

${\displaystyle (3^{3})^{3}\neq 3^{(3^{3})};}$

dla potęgowania stosuje się domyślnie notację prawostronnie łączną, tj.

${\displaystyle 3^{3^{3}}=3^{(3^{3})}=3^{27}.}$

Inne działania niełączne

• różnica zbiorów^[19] – przykładowo:

${\displaystyle (A\backslash A)\backslash A=\emptyset \backslash A=\emptyset ,}$

${\displaystyle A\backslash (A\backslash A)=A\backslash \emptyset =A;}$

• iloczyn wektorowy w trójwymiarowej przestrzeni kartezjańskiej ${\displaystyle (\mathbb {R} ^{3})}$ – na ogół^[20]:

${\displaystyle {\vec {a}}\times ({\vec {b}}\times {\vec {c}})\neq ({\vec {a}}\times {\vec {b}})\times {\vec {c}};}$

przykładu niełączności dostarcza iloczyn wersorów^[21]:

${\displaystyle ({\vec {e_{x}}}\times {\vec {e_{x}}})\times {\vec {e_{y}}}={\vec {0}}\times {\vec {e_{y}}}={\vec {0}},}$

${\displaystyle {\vec {e_{x}}}\times ({\vec {e_{x}}}\times {\vec {e_{y}}})={\vec {e_{x}}}\times {\vec {e_{z}}}=-{\vec {e_{y}}};}$

• mnożenie oktonionów^[22][23];
• dodawanie liczb zmiennoprzecinkowych^[24].

Własności

• Łączność pozwala opuszczać nawiasy przy dowolnej skończonej liczbie zmiennych; np. dla dowolnych czterech argumentów ${\displaystyle a,b,c,d}$ zachodzą równości:

${\displaystyle {\begin{aligned}&{\big (}a\diamond (b\diamond c){\big )}\diamond d=\\=&{\big (}(a\diamond b)\diamond c{\big )}\diamond d=\\=&(a\diamond b)\diamond (c\diamond d)=\\=&a\diamond {\big (}b\diamond (c\diamond d){\big )}=\\=&a\diamond {\big (}(b\diamond c)\diamond d{\big )}.\end{aligned}}}$

Każde z tych pięciu wyrażeń da się zapisać jako:

${\displaystyle a\diamond b\diamond c\diamond d.}$

• Działania na nieskończonej liczbie argumentów mają bardziej skomplikowane definicje. Czasem takie działanie może być oparte na działaniu łącznym, a mimo to być w pewnym sensie niełączne, tzn. jego wynik może zależeć od układu nawiasów. Przystępnym przykładem jest tu szereg Grandiego.
• Jeśli działanie jest łączne, to każdy element ma względem tego działania co najwyżej jeden element odwrotny^[25]. Niech ${\displaystyle e}$ oznacza element neutralny działania, a ${\displaystyle b}$ i ${\displaystyle b'}$ – elementy odwrotne do ${\displaystyle a\colon }$

${\displaystyle {\begin{aligned}a\diamond b&=b\diamond a=e=\\&=a\diamond b'=b'\diamond a.\end{aligned}}}$

Wtedy:

${\displaystyle {\begin{aligned}b'&=b'\diamond e=b'\diamond (a\diamond b)=\\&=(b'\diamond a)\diamond b=e\diamond b=b.\blacksquare \end{aligned}}}$

• Twierdzenie odwrotne do powyższego nie zachodzi. Kontrprzykładem są oktoniony – w zbiorze tych niezerowych jest jednoznaczne dzielenie, ale mnożenie nie jest łączne^[23].

• Łączność jest niezależna od przemienności – działanie może:
  • mieć obie te własności;
  • mieć tylko jedną z nich;
  • nie mieć żadnej z nich^[26].

Łączność w różnych notacjach

Przegląd

Niech ${\displaystyle \forall a,b,c\in X.}$ Wtedy łączność można zapisywać różnie:

• w notacji funkcyjnej:

${\displaystyle f(a,f(b,c))=f(f(a,b),c),}$

• w notacji przedrostkowej (beznawiasowej):

${\displaystyle \diamondsuit \,a\,\diamondsuit \,b\,c=\diamondsuit \,\diamondsuit \,a\,b\,c,}$

• w notacji przyrostkowej (beznawiasowej):

${\displaystyle a\,b\,c\,\diamondsuit \,\diamondsuit =a\,b\,\diamondsuit \,c\,\diamondsuit .}$

W powyższych trzech notacjach nie stosuje się reguły pomijania nawiasów:

• w pierwszym wypadku nawiasy są nieusuwalne; jest to w istocie odmiana notacji przedrostkowej;
• w następnych dwóch nawiasy są całkowicie zbędne. Należy jedynie odpowiednio zamieniać miejscami symbole działania i ich argumentów – por. zapis działań dwuargumentowych.

Oto wyrażenia z sekcji „Własności” w notacji przedrostkowej:

${\displaystyle {\begin{aligned}&\diamondsuit \diamondsuit a\diamondsuit bcd\\[1ex]={}&\diamondsuit \diamondsuit \diamondsuit abcd\\[1ex]={}&\diamondsuit \diamondsuit ab\diamondsuit cd\\[1ex]={}&\diamondsuit a\diamondsuit b\diamondsuit cd\\[1ex]={}&\diamondsuit a\diamondsuit \diamondsuit bcd.\end{aligned}}}$

Notacja dla działań niełącznych

W notacji wrostkowej dla działania niełącznego każde dwa argumenty (także te złożone) muszą być razem z operatorem objęte parą nawiasów (z wyjątkiem oczywiście najbardziej zewnętrznej pary argumentów). W notacji tej wszystkie nawiasy są niezbędne dla określenia kolejności wykonywanych działań. Przy większej ilości argumentów wyrażenia stają się przez to nieczytelne, np.:

${\displaystyle {\big (}a\;\diamondsuit \;((b\;\diamondsuit \;c)\;\diamondsuit \;d){\big )}\;\diamondsuit \;(e\;\diamondsuit \;f).}$

(2)

W notacji przedrostkowej powyższe wyrażenie ma postać ${\displaystyle \diamondsuit \diamondsuit a\diamondsuit \diamondsuit bcd\diamondsuit ef,}$ w notacji przyrostkowej ${\displaystyle abc\diamondsuit d\diamondsuit \diamondsuit ef\diamondsuit \diamondsuit .}$ W obu tych notacjach łączność lub niełączność działania nie ma oczywiście większego znaczenia, bowiem mimo braku nawiasów kolejność wykonywania działań jest „zakodowana” w wyrażeniu i jest możliwa do odtworzenia dzięki regułom tworzenia takich wyrażeń. Brak nawiasów nieco upraszcza zapis i przyczynia się do zwiększenia czytelności.

Notacja wrostkowa jednostronnie łączna

Ilość nawiasów notacji wrostkowej można zmniejszyć (a tym samym nieco uprościć zapis), wprowadzając notację z łącznością jednostronną. Oznacza to wybór jednej z dwóch możliwych kolejności usuwania nawiasów w wyrażeniu:

• w lewostronnej łączności dopuszcza uproszczenie: ${\displaystyle (a\diamondsuit b)\diamondsuit c=a\diamondsuit b\diamondsuit c}$ i zakazuje się usuwania nawiasów w wyrażeniu ${\displaystyle a\diamondsuit (b\diamondsuit c),}$
• w prawostronnej łączności dopuszcza uproszczenie: ${\displaystyle a\diamondsuit (b\diamondsuit c)=a\diamondsuit b\diamondsuit c}$ i zakazuje się usuwania nawiasów w wyrażeniu ${\displaystyle (a\diamondsuit b)\diamondsuit c.}$

Oczywiście kolejność usuwania nawiasów w notacji z jednostronną łącznością jest równoznaczne z odwrotną kolejnością ich przywracania (nawiasy domyślne). Np. wyrażenie ${\displaystyle a\diamondsuit b\diamondsuit c\diamondsuit d}$

• w notacji z łącznością lewostronną jest równoznaczne z wyrażeniem ${\displaystyle {\big (}(a\diamondsuit b)\diamondsuit c{\big )}\diamondsuit d,}$ czyli działania są wykonywane od lewej;
• w notacji z łącznością prawostronną jest równoznaczne z wyrażeniem ${\displaystyle a\diamondsuit {\big (}b\diamondsuit (c\diamondsuit d){\big )},}$ czyli działania są wykonywane od prawej.

Stosując notację z lewostronną łącznością, wyrażenie (2) uprości się do postaci ${\displaystyle a\diamondsuit (b\diamondsuit c\diamondsuit d)\diamondsuit (e\diamondsuit f),}$ z prawostronną do postaci ${\displaystyle (a\diamondsuit (b\diamondsuit c)\diamondsuit d)\diamondsuit e\diamondsuit f.}$

Notacja z jednostronną łącznością jest więc odmianą notacji wrostkowej, w której niektóre nawiasy można pominąć. Dla każdego działania binarnego niełącznego wybór notacji z lewostronną lub prawostronną łącznością jest całkowicie dowolny i arbitralny, ale raz dokonany wybór dla danego działania musi być utrzymany dla zachowania jednoznaczności wartościowania wyrażenia. Inaczej mówiąc, działanie binarne niełączne nie jest ani lewostronnie, ani prawostronnie łączne. Stwierdzenie, że jakieś działanie jest lewo/prawostronnie łączne oznacza, że wobec tego działania stosuje się notację wrostkową odpowiednio z lewo/prawostronną łącznością.

Rola w algebrze wyższej

Diagram przemienny przedstawiający łączność złożenia strzałek (morfizmów): ${\displaystyle f\circ (g\circ h)}$${\displaystyle \ =\ }$${\displaystyle (f\circ g)\circ h.}$ To jedno z podstawowych założeń w teorii kategorii

Diagram przemienny pokazujący, że działanie ${\displaystyle \diamond }$ jest łączne. ${\displaystyle \times }$ oznacza iloczyn kartezjański, a ${\displaystyle {\text{id}}_{X}}$ – funkcję tożsamościową

Jak wspomniano we wcześniejszych sekcjach, łączność zachodzi w niektórych kontekstach matematyki wyższej jak algebra zbiorów, liczby zespolone, hiperzespolone i macierze. Twierdzenie Frobeniusa o algebrach mówi o możliwych uogólnieniach liczb rzeczywistych z zachowaniem podstawowych własności działań arytmetycznych. Mówi między innymi, że wśród tego typu rozszerzeń liczb zespolonych istnieje tylko jedno z łącznością mnożenia: kwaterniony^[27].

Łączność występuje też w definicjach różnych struktur algebraicznych badanych przez algebrę abstrakcyjną. Przykłady to:

• grupy^[28] i ich uogólnienia jak monoidy^[29], półgrupy^[30] i kategorie^[31];
• ciała^[32] i ich uogólnienia jak pierścienie^[33] i półpierścienie^[34][35];
• algebry Boole’a^[36] i ogólniejsze kraty^[37], półkraty^[38] oraz pasy^[39].

W definicji przestrzeni liniowych pojawia się równość analogiczna do tej opisującej łączność^[40]. Ta równość także bywa nazywana łącznością^[41][42]:

${\displaystyle (\alpha \beta ){\vec {v}}=\alpha (\beta {\vec {v}}).}$

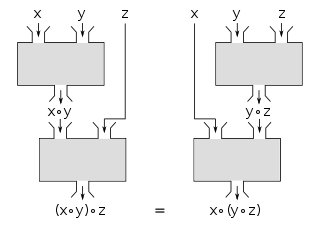
Algebra wyższa nie tylko korzysta z pojęcia łączności. Pozwala je też równoważnie zdefiniować przez złożenie funkcji – pokazuje to diagram przemienny obok, z iloczynami kartezjańskimi^[43].

Zobacz też

• Algorytm szybkiego potęgowania
• Problem nawiasowania ciągu macierzy
• Test łączności Lighta

Uwagi

1. przy standardowym założeniu, że wyrazami macierzy są liczby rzeczywiste, zespolone lub inne elementy z łącznym dodawaniem. Wyjątki od tej reguły to np. liczby zmiennoprzecinkowe, o czym pisze odpowiednia sekcja
2. mnożenie jest też możliwe dla niektórych macierzy o różnych wymiarach, ale przy tym ogólnym rozumieniu nie jest to ściśle rozumiane działanie dwuargumentowe – nie jest określone dla dowolnej pary macierzy