热门问题
时间线
聊天
视角
正图形列表
维基媒体列表条目 来自维基百科,自由的百科全书
Remove ads
此页面列出了所有的欧几里得空间、双曲空间和球形空间的正图形或正多胞形。施莱夫利符号可以描述每一个正图形或正多胞形,他被广泛使用如下面的每一个紧凑的参考名称。
正图形或正多胞形可由其维度分类,也可以分成凸、非凸(星形、扭歪、复合或凹)和无穷等形式。非凸形式(或凹形式)使用与凸形式相同的顶点,但面(或边)有相交。无限的形式则是在一较低维的欧几里得空间中密铺(镶嵌或堆砌)。
无限的形式可以扩展到密铺双曲空间。双曲空间是和正常的空间有相同的规模,但平行线在一定的距离内会分岔得越来越远。这使得顶点值可以存在负角度的缺陷,例如制作一个由个正三角形组成的顶点,它们可以被平放。它不能在普通平面上完成的,但可以在一个双曲平面上构造。
Remove ads
概观
请注意,平面密铺和双曲密铺的维数比预期多一维。这是因为它们是有限多胞形在不同维度的类比:凸正n胞形可以看作(n−1)维球面空间的镶嵌。因此,欧几里德平面的三个正镶嵌图(正三角形镶嵌、正方形镶嵌和正六边形镶嵌)列在第三维度而不是第二维下。
Remove ads
零维或以下的正图形

在维数为零的空间能存在的多胞形只有点[3],无法有其他几何或拓朴组合,而维数比零更低则是在抽象理论中的虚无多胞形(英语:Null polytope)代表一种空集合,在抽象理论中被看作是一种负一维的多胞形[4],但其是一种抽象多胞形。然而,在数学上,零维空间是按以下的不等价定义之一,维数为零的拓扑空间:按覆盖维数的概念,一个拓扑空间是零维空间,若空间的任何开覆盖,都有一个加细,使得空间内每一点,都在这个加细的恰好一个开集内;或者按小归纳维数的概念,一个拓扑空间是零维空间,若空间有一个由闭开集组成的基。这两个概念对可分可度量化空间为等价[5][6]。而负一维空间仅是在抽象理论表示一个比零维多胞形更低维度的一个元词。
依据正图形的定义,一个多胞形必须要具备严格的标记可递特性,对于该几何体内所有同维度的元素(如:点、线、面)都完全具有相同的性质,并且每一个元素皆为一个正图形,而零维多胞形的元素仅有{F−1, F0}、负一维多胞形的元素仅有{F−1},几何上所有零维多胞形都是正多胞形,一般地,n维正图形被定义为有正维面[(n − 1)-表面]和正顶点图,这两个条件已经能充分地保证所有面、所有顶点都是相似的,但这一定义并不适用于抽象多胞形,而负一维的多胞形的仅有一种抽象多胞形。
另外,正零边形也可以视为零维或以下的正图形,或看做是虚无多胞形(英语:Null polytope)。
Remove ads
一维正图形

|
考克斯特记号终结点代表一个镜射面,周围有环的节点表示其不位于一个平面。 ditel, { }, |
在维数为一的一维空间里存在的多胞形是由两个端点包围住的一个封闭一维空间,即线段。在定义上,这个一维多胞形(或称1-多胞形)在施莱夫利符号中以: { } 表示[8][9],而在考克斯特记号中则以一个有环的节点:![]() 表示[7]。诺曼·约翰逊将之称为ditel,并在施莱夫利符号中以{ }表示[10]。依据正图形的定义,一个多胞形必须要具备严格的标记可递特性,对于该几何体内所有同维度的元素(如:点、线、面)都完全具有相同的性质,并且每一个元素皆为一个正图形,而一维多胞形的旗包含{F−1, F0, F1}、其元素仅有{F−1, A, B, AB},其中,A、B为线段两端点,由于几何上所有零维多胞形都是正多胞形,因此所有的线段都会符合标记可递特以及所有同维度的元素(如:点、线、面)都完全具有相同的性质,并且每一个元素皆为一个正图形,因此在几何上所有的一维多胞形都是正多胞形。
表示[7]。诺曼·约翰逊将之称为ditel,并在施莱夫利符号中以{ }表示[10]。依据正图形的定义,一个多胞形必须要具备严格的标记可递特性,对于该几何体内所有同维度的元素(如:点、线、面)都完全具有相同的性质,并且每一个元素皆为一个正图形,而一维多胞形的旗包含{F−1, F0, F1}、其元素仅有{F−1, A, B, AB},其中,A、B为线段两端点,由于几何上所有零维多胞形都是正多胞形,因此所有的线段都会符合标记可递特以及所有同维度的元素(如:点、线、面)都完全具有相同的性质,并且每一个元素皆为一个正图形,因此在几何上所有的一维多胞形都是正多胞形。
虽然线段做为一个多胞形是微不足道的,但它似乎是多边形和其他更高维度图形形成边缘所需的一个元素[11]。在一维以及以下(包括一维、零维、负一维)空间中的多胞形都是正多胞形,包含了一维的线段、零维的点和负一维的抽象虚无多胞形都是组成多边形和其他更高维度图形的重要元素之一,比如一维的线段组成多边形的边、零维的点组成多边形的顶点以及代表集合子集中空集合的抽象虚无多胞形都是多边形的组成元素(子集),依据正图形定义,若这些低为度不存在正图形,则也不会有正多边形和其他更高维度的正图形。
在柱体的定义里,线段(一维)可以被看做是点(零维)的柱体,在施莱夫利符号中以{ }×{p}表示,而在考克斯特记号中则以笛卡儿积的形式![]()
![]()
![]()
![]()
![]() 表示一个线段和多边形[12]。
表示一个线段和多边形[12]。
二维正多边形
- 边数较大的正多边形
Remove ads
Remove ads
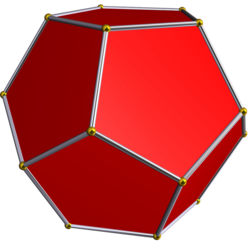
三维正图形
Remove ads
在球面几何学中,多面形 {2,n} 和多边形二面体 {n,2} 以及一面体 {1,1} 也可以被视为是一种正多面体(正球面镶嵌)。
他们包括:
Remove ads
考克斯特在他的论文《三维和四维空间的正扭歪多面体极其类似物》[24]中列出了较多的一系列扭歪多面体,其中有四种是正图形。
四维正图形
在四维空间中存在6种凸正图形。
四维的扭歪多胞体是一些位于五维或以上的扭歪图形。
五维正图形
 五维正六胞体 |
 五维超正方体 |
 五维正三十二胞体 |
六维正图形
 六维正七胞体 |
 六维超立方体 |
 六维正六十四胞体 |
七维正图形
 七维正八胞体 |
 七维超立方体 |
 七维正一百二十八胞体 |
七维以上正图形
从五维开始,凸正多胞体都只有三种[25]。
 八维单体 |
 八维超立方体 |
 八维正轴体 |
 九维单体 |
 九维超立方体 |
 九维正轴体 |
 十维单体 |
 十维超立方体 |
 十维正轴体 |
 十一维单体 |
 十一维超立方体 |
 十一维正轴体 |
 十二维单体 |
 十二正轴体 |
从五维开始就都不存在任何非凸多胞形。
正无穷多胞形
对应的欧几里得密铺只有一种,密铺于一维欧几里得空间,即直线,即正无限边形。其施莱夫利符号以{∞}表示、考克斯特符号以![]()
![]()
![]() 表示。
表示。
该镶嵌是由一维正图形“线段”(即二维二边形)完成一维欧几里得空间的密铺。
对应的双曲密铺只有一种,即由一维正图形“线段”完成一维罗氏空间(即二维双曲线)的密铺,类似于无限边形,称为超无限边形,但又因为它是发散的,因此又称为伪多边形。在施莱夫利符号以{iπ/λ}表示、考克斯特符号以![]()
![]()
![]() 表示。
表示。

三维空间中只有一种正堆砌体,即立方体堆砌{4, 3, 4}:[7]
 超立方体堆砌 |
 正十六胞体堆砌 |
 正二十四胞体堆砌 |
五维空间的正堆砌仅有五维超立方体堆砌{4,3,3,3,4}[26]
六维或以上的维度皆不存在紧空间与仿紧空间的双曲堆砌。不过,任何的{p,q,r,s,...}形式(其中p,q,r,s,...是大于二的自然数或无限大)以上并不包括n维空间的非紧镶嵌。
复合正图形
 2{2} |
3{2} |
 4{2} |
5{2} |
 6{2} |
7{2} |
 8{2} |
9{2} |
 10{2} |
 11{2} |
 12{2} |
 13{2} |
 14{2} |
 15{2} | |
2{3} |
 3{3} |
 4{3} |
 5{3} |
6{3} |
 7{3} |
 8{3} |
 9{3} |
 10{3} |
 2{4} |
 3{4} |
 4{4} |
 5{4} |
 6{4} |
 7{4} |
2{5} |
 3{5} |
 4{5} |
 5{5} |
 6{5} |
2{5/2} |
 3{5/2} |
 4{5/2} |
 5{5/2} |
 6{5/2} |
 2{6} |
3{6} |
 4{6} |
 5{6} | |
2{7} |
 3{7} |
 4{7} |
2{7/2} |
 3{7/2} |
 4{7/2} |
2{7/3} |
 3{7/3} |
 4{7/3} |
 2{8} |
 3{8} |
 2{8/3} |
 3{8/3} | ||
2{9} |
 3{9} |
2{9/2} |
 3{9/2} |
2{9/4} |
 3{9/4} |
 2{10} |
 3{10} |
 2{10/3} |
 3{10/3} | |||||
 2{11} |
 2{11/2} |
 2{11/3} |
 2{11/4} |
 2{11/5} |
 2{12} |
 2{12/5} |
 2{13} |
 2{13/2} |
 2{13/3} |
 2{13/4} |
 2{13/5} |
 2{13/6} | ||
 2{14} |
 2{14/3} |
 2{14/5} |
 2{15} |
 2{15/2} |
 2{15/4} |
 2{15/7} |
抽象正图形
参见
注释
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads















































































































































 ,
,  ...
...

































































































