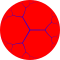
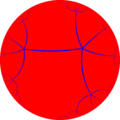
Uniform tiling symmetry mutations

In geometry, a symmetry mutation is a mapping of fundamental domains between two symmetry groups.^[1] They are compactly expressed in orbifold notation. These mutations can occur from spherical tilings to Euclidean tilings to hyperbolic tilings. Hyperbolic tilings can also be divided between compact, paracompact and divergent cases.

Example *n32 symmetry mutations

Spherical tilings (n = 3..5)
*332	*432	*532
Euclidean plane tiling (n = 6)
*632
Hyperbolic plane tilings (n = 7...∞)
*732	*832	... *∞32

The uniform tilings are the simplest application of these mutations, although more complex patterns can be expressed within a fundamental domain.

This article expressed progressive sequences of uniform tilings within symmetry families.

Mutations of orbifolds

Orbifolds with the same structure can be mutated between different symmetry classes, including across curvature domains from spherical, to Euclidean to hyperbolic. This table shows mutation classes.^[1] This table is not complete for possible hyperbolic orbifolds.

Orbifold	Spherical	Euclidean	Hyperbolic
o	-	o	-
pp	22, 33 ...	∞∞	-
*pp	*22, *33 ...	*∞∞	-
p*	2*, 3* ...	∞*	-
p×	2×, 3× ...	∞×
**	-	**	-
*×	-	*×	-
××	-	××	-
ppp	222	333	444 ...
pp*	-	22*	33* ...
pp×	-	22×	33×, 44× ...
pqq	222, 322 ... , 233	244	255 ..., 433 ...
pqr	234, 235	236	237 ..., 245 ...
pq*	-	-	23*, 24* ...
pq×	-	-	23×, 24× ...
p*q	2*2, 2*3 ...	3*3, 4*2	5*2 5*3 ..., 4*3, 4*4 ..., 3*4, 3*5 ...
*p*	-	-	*2* ...
*p×	-	-	*2× ...
pppp	-	2222	3333 ...
pppq	-	-	2223...
ppqq	-	-	2233
pp*p	-	-	22*2 ...
p*qr	-	2*22	3*22 ..., 2*32 ...
*ppp	*222	*333	*444 ...
*pqq	*p22, *233	*244	*255 ..., *344...
*pqr	*234, *235	*236	*237..., *245..., *345 ...
p*ppp	-	-	2*222
*pqrs	-	*2222	*2223...
*ppppp	-	-	*22222 ...
...

*n22 symmetry

Regular tilings

Family of regular hosohedra · *n22 symmetry mutations of regular hosohedral tilings: nn

Space	Spherical						Euclidean
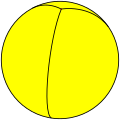
Tiling name	Henagonal hosohedron	Digonal hosohedron	Trigonal hosohedron	Square hosohedron	Pentagonal hosohedron	...	Apeirogonal hosohedron
Tiling image						...
Schläfli symbol	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	...	{2,∞}
Coxeter diagram						...
Faces and edges	1	2	3	4	5	...	∞
Vertices	2	2	2	2	2	...	2
Vertex config.	2	2.2	23	24	25	...	2∞

Family of regular dihedra · *n22 symmetry mutations of regular dihedral tilings: nn

Space	Spherical						Euclidean
Tiling name	Monogonal dihedron	Digonal dihedron	Trigonal dihedron	Square dihedron	Pentagonal dihedron	...	Apeirogonal dihedron
Tiling image						...
Schläfli symbol	{1,2}	{2,2}	{3,2}	{4,2}	{5,2}	...	{∞,2}
Coxeter diagram						...
Faces	2 {1}	2 {2}	2 {3}	2 {4}	2 {5}	...	2 {∞}
Edges and vertices	1	2	3	4	5	...	∞
Vertex config.	1.1	2.2	3.3	4.4	5.5	...	∞.∞

Prism tilings

*n22 symmetry mutations of uniform prisms: n.4.4

Space	Spherical										Euclidean
Tiling
Config.	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...∞.4.4

Antiprism tilings

*n22 symmetry mutations of antiprism tilings: Vn.3.3.3

Space	Spherical							Euclidean
Tiling
Config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	...∞.3.3.3

*n32 symmetry

Regular tilings

*n32 symmetry mutation of regular tilings: {3,n} v t e
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

*n32 symmetry mutation of regular tilings: {n,3} v t e
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Truncated tilings

*n32 symmetry mutation of truncated tilings: t{n,3} v t e
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Symbol	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Triakis figures
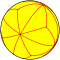Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

*n32 symmetry mutation of truncated tilings: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
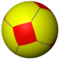
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
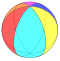Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Quasiregular tilings

Quasiregular tilings: (3.n)2 v t e
Sym. *n32 [n,3]	Spherical			Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] p6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figure
Figure
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2	(3.12i)2	(3.9i)2	(3.6i)2
Schläfli	r{3,3}	r{3,4}	r{3,5}	r{3,6}	r{3,7}	r{3,8}	r{3,∞}	r{3,12i}	r{3,9i}	r{3,6i}
Coxeter
Dual uniform figures
Dual conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

Symmetry mutations of dual quasiregular tilings: V(3.n)2
*n32	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

Expanded tilings

*n32 symmetry mutation of expanded tilings: 3.4.n.4 v t e
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figure
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4	3.4.12i.4	3.4.9i.4	3.4.6i.4

*n32 symmetry mutation of dual expanded tilings: V3.4.n.4

Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure Config.	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

Omnitruncated tilings

*n32 symmetry mutation of omnitruncated tilings: 4.6.2n v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Snub tilings

n32 symmetry mutations of snub tilings: 3.3.3.3.n v t e
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
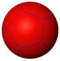Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

*n42 symmetry

Regular tilings

*n42 symmetry mutation of regular tilings: {4,n} v t e
Spherical	Euclidean	Compact hyperbolic				Paracompact
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4,∞}

*n42 symmetry mutation of regular tilings: {n,4} v t e
Spherical		Euclidean	Hyperbolic tilings
24	34	44	54	64	74	84	...∞4

Quasiregular tilings

*n42 symmetry mutations of quasiregular tilings: (4.n)2 v t e
Symmetry *4n2 [n,4]	Spherical	Euclidean	Compact hyperbolic				Paracompact	Noncompact
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[ni,4]
Figures
Config.	(4.3)2	(4.4)2	(4.5)2	(4.6)2	(4.7)2	(4.8)2	(4.∞)2	(4.ni)2

*n42 symmetry mutations of quasiregular dual tilings: V(4.n)2
Symmetry *4n2 [n,4]	Spherical	Euclidean	Compact hyperbolic				Paracompact	Noncompact
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[iπ/λ,4]
Tiling   Conf.	V4.3.4.3	V4.4.4.4	V4.5.4.5	V4.6.4.6	V4.7.4.7	V4.8.4.8	V4.∞.4.∞	V4.∞.4.∞

Truncated tilings

*n42 symmetry mutation of truncated tilings: 4.2n.2n v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
n-kis figures
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

*n42 symmetry mutation of truncated tilings: n.8.8 v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracompact
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures
Config.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
n-kis figures
Config.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

Expanded tilings

*n42 symmetry mutation of expanded tilings: n.4.4.4 v t e
Symmetry [n,4], (*n42)	Spherical	Euclidean	Compact hyperbolic				Paracomp.
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]	*∞42 [∞,4]
Expanded figures
Config.	3.4.4.4	4.4.4.4	5.4.4.4	6.4.4.4	7.4.4.4	8.4.4.4	∞.4.4.4
Rhombic figures config.	V3.4.4.4	V4.4.4.4	V5.4.4.4	V6.4.4.4	V7.4.4.4	V8.4.4.4	V∞.4.4.4

Omnitruncated tilings

*n42 symmetry mutation of omnitruncated tilings: 4.8.2n v t e
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

Snub tilings

4n2 symmetry mutations of snub tilings: 3.3.4.3.n v t e
Symmetry 4n2	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	242	342	442	542	642	742	842	∞42
Snub figures
Config.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Gyro figures
Config.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

*n52 symmetry

Regular tilings

*n52 symmetry mutation of truncated tilings: 5ⁿ

Sphere	Hyperbolic plane
{5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}	...{5,∞}

*n62 symmetry

Regular tilings

*n62 symmetry mutation of regular tilings: {6,n} v t e
Spherical	Euclidean	Hyperbolic tilings
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

*n82 symmetry

Regular tilings

n82 symmetry mutations of regular tilings: 8ⁿ

• v
• t
• e

Space	Spherical	Compact hyperbolic						Paracompact
Tiling
Config.	8.8	83	84	85	86	87	88	...8∞