正多面体列表

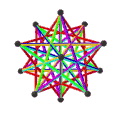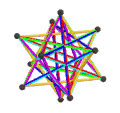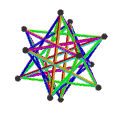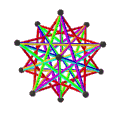
在几何学中，正多面体是指各面都是全等的正多边形且每一个顶点所接的面数都是一样的多面体。除了五种凸正多面体（帕雷托立体）外，亦有其他能符合上述条件的立体，例如四种星形正多面体（开普勒－庞索立体）^[2]。

部分的正多面体

主条目：正多面体

在不考虑其他空间（如双曲空间、复数空间）的情况下，麦克马伦在其论文中共整理并列出了48种正多面体^[3]。

概述

所有正多面体皆可以使用施莱夫利符号来表示，其可以计为{n, m}。其中n表示构成面的顶点数，m则表示与顶点相邻的多边形数量。在中文语境中，一般被大众认知的正多面体通常代表只有五种的凸正多面体，又称为帕雷托立体，其包括了正四面体、立方体、正八面体、正十二面体和正二十面体^[4]。然而在定义上，正多面体仅指每个面是正多边形、每条边等长每个角等角且每面全等的多面体，而符合上述定义的多面体不一定是凸多面体，也可能是星形多面体^[5]、抽象多面体^[6]或扭歪多面体^[7]等。这些多面体除了五种凸正多面体外，还有四种非凸正多面体（克普勒–庞索立体）、五种抽象正多面体和五种复合正多面体。

帕雷托立体	正四面体、 立方体、 正八面体、 正十二面体、 正二十面体
开普勒－庞索立体	小星形十二面体、 大十二面体、 大星形十二面体、 大二十面体
复合正多面体	星形八面体、 五复合正四面体、 十复合正四面体、 五复合立方体、 五复合正八面体
正扭歪无限面体	四角六片四角孔扭歪无限面体、 六角四片四角孔扭歪无限面体、 六角六片三角孔扭歪无限面体
正扭歪多面体	四角六片三角孔扭歪正三十面体、 六角四片三角孔扭歪正二十面体、 四角八片三角孔扭歪正二百八十八面体、 八角四片三角孔扭歪正一百四十四面体
复空间正多面体	黑塞二十七面体、 双黑塞二十七面体、 截半黑塞二十七面体
正多面体半形	立方体半形、 八面体半形、 十二面体半形、 二十面体半形
依面的个数	正零面体（0、 空多胞形）、 正一面体（1）、 正二面体（2、 多边形二面体）、 正三面体（3、 立方体半形）、 正四面体（4、 正四面体、 八面体半形）、 正六面体（6、 立方体、 十二面体半形）、 正八面体（8、 正八面体、 星形八面体）、 正十面体（10、 二十面体半形）、 正十二面体（12、 正十二面体、 小星形十二面体、 大十二面体、 大星形十二面体）、 正二十面体（20、 正二十面体、 大二十面体、 六角四片三角孔扭歪正二十面体、 五复合正四面体）、 正二十七面体（27、 黑塞二十七面体）、 正三十面体（30、 四角六片三角孔扭歪正三十面体、 五复合立方体）、 正四十面体（40、 十复合正四面体、 五复合正八面体）、 正五十四面体（54、 截半黑塞二十七面体）、 正七十二面体（72、 双黑塞二十七面体）、 正一百四十四面体（144、 八角四片三角孔扭歪正一百四十四面体）、 正二百八十八面体（288、 四角八片三角孔扭歪正二百八十八面体）、 正无限面体（∞、 正镶嵌图、 扭歪无限面体、 § 双曲无限面体）
依组成面	§ 二角形、 § 正三角形、 § 正方形、 § 五边形 （ § 五边形、 § 正五角星形）、 § 六边形、 § 七边形、 § 八边形、 § 无限边形

列表

下表列出了所有标记可以在其对称性上传递的多面体，换句话说，即该多面体皆同时具有等边、等角和等面的特性。

分类	名称 施氏符号	子类	图像	顶点	边	面	面的位置	顶点图	X	对偶多面体	对称性
凸正 多面体 帕雷托立体	正四面体 {3,3}4	四面体		4	6条棱	4个正三角形		33	2	（自身对偶）	Td [3,3] (*332)
	立方体 {4,3}6	六面体		8	12条棱	6个正方形		43	2	正八面体	Oh [4,3] (*432)
	正八面体 {3,4}6	八面体		6	12条棱	8个正三角形		34	2	立方体	Oh [4,3] (*432)
	正十二面体 {5,3}10	十二面体		20	30条棱	12个正五边形		53	2	正二十面体	Ih [5,3] (*532)
	正二十面体 {3,5}10	二十面体		12	30条棱	20个正三角形		35	2	正十二面体	Ih [5,3] (*532)
星形 正多面体 开普勒 庞索立体	小星形十二面体 {5/2,5}6	十二面体		12	30条棱	12个正五角星		(5/2)5	-6	大十二面体	Ih [5,3] (*532)
	大十二面体 {5,5/2}6	十二面体		12	30条棱	12个正五边形		(55)/2	-6	小星形十二面体	Ih [5,3] (*532)
	大星形十二面体 {5/2,3}10/3	十二面体		20	30条棱	12个正五角星		(5/2)3	2	大二十面体	Ih [5,3] (*532)
	大二十面体 {3,5/2}10/3	二十面体		12	30条棱	20个正三角形		(35)/2	2	大星形十二面体	Ih [5,3] (*532)
复合正多面体	星形八面体 {{3,3}}、 a{4,3} ß{2,4}、 ßr{2,2} ∪ 、 、 、	星形八面体 二复合四面体		8	12条棱	8个正三角形			4	（自身对偶）	Oh [4,3]
	五复合正四面体	星形二十面体		20	30条棱	20个正三角形			10	（自身对偶）	手性（英语：Chirality (mathematics)） 二十面 体群（英语：Icosahedral symmetry） (I)
	十复合正四面体 2{5,3}[10{3,3}]2{3,5}[8]	星形四十面体		20	60条棱	40个正三角形			0	（自身对偶）	${\displaystyle I_{h}}$群
	五复合立方体 2{5,3}[5{4,3}][9][8]	星形三十面体		20	60条棱	30个正方形			-10	五复合正八面体	${\displaystyle I_{h}}$群
	五复合正八面体 [5{3,4}]2{3,5}[9][8]	星形四十面体		30	60条棱	40个正三角形			10	五复合立方体	${\displaystyle I_{h}}$群
正扭歪 无限面体	四角六片四角孔 扭歪无限面体 {4,6|4}	扭歪无限面体		∞	∞条棱	正方形 孔洞： 正方形		{3}#{ }		六角四片 四角孔 扭歪 无限面体	[[4,3,4]] [[4,3,4]+]
	六角四片四角孔 扭歪无限面体 {6,4|4}	扭歪无限面体		∞	∞条棱	正六边形 孔洞： 正方形		{4}#{ }		四角六片 四角孔 扭歪 无限面体	[[4,3,4]] [[4,3,4]+]
	六角六片三角孔 扭歪无限面体 {6,6|3}	扭歪无限面体		∞	∞条棱	正六边形 孔洞： 正三角形		{3}#{ }		（自身对偶）	[[3[4]]] [[3[4]]+]
四维空间 扭歪正多面体	四角六片三角孔 扭歪正三十面体 {4,6|3}	扭歪三十面体		20	60条棱	30个正方形 孔洞： 正三角形		{3}#{ }	-10	六角四片 三角孔 扭歪正 二十面体
	六角四片三角孔 扭歪正二十面体 {6,4|3}	扭歪二十面体		30	60条棱	20个正六边形 孔洞： 正三角形		{4}#{ }	-10	四角六片 三角孔 扭歪正 三十面体
	四角八片三角孔 扭歪正 二百八十八面体 {4,8|3}	扭歪288面体		144	576条棱	288个正方形 孔洞： 正三角形			-144	八角四片 三角孔 扭歪正 144面体
	八角四片三角孔 扭歪正 一百四十四面体 {8,4|3}	扭歪144面体		288	576条棱	144个正八边形 孔洞： 正三角形			-144	四角八片 三角孔 扭歪正 288面体
	四角四片p角孔 扭歪正 一百四十四面体 {4,4|p}	扭歪p2面体		p2	2p2条棱	p2个正方形 孔洞： 正p边形
${\displaystyle \mathbb {C} ^{3}}$复空间 正多面体	2{3}2{4}p	复p3面体		3p	3p2条棱	p3个正三角形		2{4}p
	p{4}2{3}2	复3p面体		p3	3p2条p元棱	3p个p{4}2		正三角形
	黑塞二十七面体 3{3}3{3}3	复二十七面体		27	72条3元棱	27个3{3}3		3{3}3		（自身对偶）
	双黑塞二十七面体 2{4}3{3}3	复七十二面体		54	216条3元棱	72个2{4}3		3{3}3		截半黑塞二十七面体
	截半黑塞二十七面体 3{3}3{4}2	复五十四面体		72	216条3元棱	54个3{3}3		3{4}2（英语：3-3_duoprism#Related_complex_polygons）		双黑塞二十七面体
实射影 平面的 正多面体 多面体半形	立方体半形 {3,3}/2 {3,3}3	抽象三面体		4	6条棱	3个正方形			1	八面体半形	${\displaystyle S_{4}}$群
	八面体半形 {3,4}/2 {3,4}3	抽象四面体		3	6条棱	4个正三角形			1	立方体半形	${\displaystyle S_{4}}$群
	十二面体半形 {5,3}/2 {5,3}5	抽象六面体		10	15条棱	6个正五边形			1	二十面体半形	${\displaystyle A_{5}}$群
	二十面体半形 {3,5}/2 {3,5}5	抽象十面体		6	15条棱	10个正三角形			1	十二面体半形	${\displaystyle A_{5}}$群
皮特里 对偶	皮特里正四面体 {3,3}π {4,3}3	拓朴三面体		4	6条棱	3个正扭歪四边形
	皮特里立方体 {4,3}π {6,3}4	拓朴四面体		8	12条棱	4个正扭歪六边形
	皮特里正八面体 {3,4}π {6,4}3	拓朴四面体		6	12条棱	4个正扭歪六边形
	皮特里正十二面体 {5,3}π {10,3}5	拓朴六面体		20	30条棱	6个正扭歪十边形
	皮特里正二十面体 {3,5}π {10,5}3	拓朴六面体		12	30条棱	6个正扭歪十边形
	皮特里小星形十二面体 {5/2,5}π {6,5}5/2	拓朴十面体		12	30条棱	10个正扭歪六边形
	皮特里大十二面体 {5,5/2}π {6,5/2}5	拓朴十面体		12	30条棱	10个正扭歪六边形
	皮特里大星形十二面体 {5/2,3}π {10/3,3}5/2	拓朴六面体		20	30条棱	6个正扭歪十角星
	皮特里大二十面体 {3,5/2}π {10/3,5/2}3	拓朴六面体		12	30条棱	6个正扭歪十角星

无穷集合的正多面体

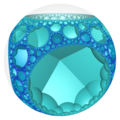
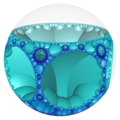
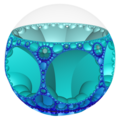
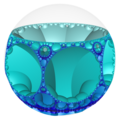
大部分的正多面体都只有有限个，如凸正多面体5个^[4]、星形多面体4个^[5]、正扭歪无限面体3个^[10]与难以良好具像化的抽象正多面体5个^[6]等。然而在部分正多面体的种类有无穷多个，如同正多边形的边数可以无穷上升一般，例如除了帕雷托立体、黑塞二十七面体、双黑塞二十七面体与截半黑塞二十七面体之外的复正多面体^[12]，或内接于双曲仿紧空间堆砌中的极限球（英语：Horosphere）上的双曲镶嵌^[13]等几何结构。

双曲无限面体

图为三阶七边形镶嵌蜂巢体在三维庞加莱球体投影的结果之旋转透视图，其中每一个凹陷进去的弧形有棱有角部分为一个内接于双曲空间中的超极限球上的正七边形镶嵌^[14]。

三阶六边形镶嵌蜂巢体{6,3,3}中的正六边形镶嵌{6,3}胞。其顶点皆位于该双曲空间极限球（英语：Horosphere）上。这时可以将这个结构视为一个双曲空间的正多面体。

在几何学中，平面镶嵌可以被视为多面的的一种退化成平面的退化形式，即无限面体^[15]。然而谝面镶嵌或双曲镶嵌可以用类似多面体堆砌填充三为欧氏空间的方法来填满双曲空间，这种结构称为蜂巢体^[16]，在这种情况下，蜂巢体中的每一个胞皆为一个平面镶嵌或双曲镶嵌^[14]，即前面所述的退化多面体或无限面体^[17]。这些退化的几何结构由于形成双曲空间蜂巢体可以内接在一个双曲极限球（即只与单一双曲无穷远点相交的双曲空间球体）^[18]或双曲超极限球（无法交于单一双曲无穷远点的双曲空间球体）^[19]上，因此，此时也能把此结构视为一个双曲空间的多面体，当这个多面体具有正多面体性质时，也可以称为一种广义的正多面体，例如六边形镶嵌蜂巢体中的六边形镶嵌^[20]或三阶七边形镶嵌蜂巢体中的正七边形镶嵌^[14]。

三种平面正镶嵌图以及其对应的双曲无限面体范例

镶嵌图	{3,6} 正三角形镶嵌	{4,4} 正方形镶嵌	{6,3} 正六边形镶嵌
以该镶嵌图为胞 的双曲空间蜂巢体	{3,6,4}（英语：Order-6-4 triangular honeycomb）	{4,4,5}（英语：Order-4-5 square_honeycomb）	{6,3,3}

正三角形组成的双曲无限面体

镶嵌图	{3,6} 六阶三角形镶嵌	{3,7} 七阶三角形镶嵌	{3,8} 八阶三角形镶嵌	...	{3,∞} 无限阶三角形镶嵌
以该镶嵌图为胞 的双曲空间蜂巢体	{3,6,4 }（英语：Order-6-4 triangular honeycomb）	{3,7,3}（英语：Order-7-3 triangular honeycomb）	{3,8,3}（英语：Order-8-3 triangular honeycomb）		{3,∞,3}

正方形组成的双曲无限面体

镶嵌图	{4,4} 四阶正方形镶嵌	{4,5} 五阶正方形镶嵌	{4,6} 六阶正方形镶嵌	{4,7} 七阶正方形镶嵌	{4,8} 八阶正方形镶嵌	...	{4,∞} 无限阶正方形镶嵌
以该镶嵌图为胞 的双曲空间蜂巢体	{4,4,5 }（英语：Order-4-5 square honeycomb）	{4,5,3}（英语：Order-5-3 square honeycomb）	{4,6,3}（英语：Order-6-3 square honeycomb）	{4,7,3}（英语：Order-7-3 square honeycomb）	{4,8,3}（英语：Order-8-3 square honeycomb）		{4,∞,3}

正五边形组成的双曲无限面体

镶嵌图	{5,4} 四阶五边形镶嵌	{5,5} 五阶五边形镶嵌	{5,6} 六阶五边形镶嵌	{5,7} 七阶五边形镶嵌	{5,8} （英语：Order-8 pentagonal tiling）八阶五边形镶嵌（英语：Order-8 pentagonal tiling）	...	{5,∞} 无限阶五边形镶嵌
以该镶嵌图为胞 的双曲空间蜂巢体	{5,4,3 }（英语：Order-4-3 pentagonal honeycomb）	{5,5,3}（英语：Order-5-3 pentagonal honeycomb）	{5,6,3}（英语：Order-6-3 pentagonal honeycomb）	{5,7,3}（英语：Order-7-3 pentagonal honeycomb）	{5,8,3}（英语：Order-8-3 pentagonal honeycomb）		{5,∞,3}

正六边形组成的双曲无限面体

镶嵌图	{6,3} 三阶六边形镶嵌	{6,4} 四阶六边形镶嵌	{6,5} 五阶六边形镶嵌	{6,6} 六阶六边形镶嵌	{6,7} 七阶六边形镶嵌	{6,8} 八阶六边形镶嵌	...	{6,∞} （英语：Infinite-order_hexagonal_tiling）无限阶六边形镶嵌（英语：Infinite-order_hexagonal_tiling）
以该镶嵌图为胞 的双曲空间蜂巢体	{6,3,3}	{6,4,3}	{6,5,3}	{6,6,3}	{6,7,3}	{6,8,3}		{6,∞,3}

正七边形组成的双曲无限面体

镶嵌图	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}	...	{7,∞}
以该镶嵌图为胞 的双曲空间蜂巢体	{7,3,3}	{7,4,3}	{7,5,3}

正八边形组成的双曲无限面体

镶嵌图	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}	...	{8,∞}
以该镶嵌图为胞 的双曲空间蜂巢体	{8,3,3}	{8,4,3}	{8,5,3}

正无限边形组成的双曲无限面体

在双曲空间的无限边形又称为超无限边形或伪多边形^[21]。

镶嵌图	{∞,3}	{∞,4}	{∞,5}	{∞,6}（英语：Order-6_apeirogonal_tiling）	{∞,7}（英语：Order-7_apeirogonal_tiling）	{∞,8}（英语：Order-8_apeirogonal_tiling）	...	{∞,∞}
以该镶嵌图为胞 的双曲空间蜂巢体	{∞,3,3}	{∞,4,3}	{∞,5,3}	{∞,6,3}	{∞,7,3}	{∞,8,3}		{∞,∞,3}

多面形与多边形二面体

参见：多面形和多边形二面体

二角形二面体 {2,2}	正三角形二面体 {3,2}	正方形二面体 {4,2}	正五边形二面体 {5,2}	正六边形二面体 {6,2}	...	{n,2}
正二面形 {2,2}	正三面形 {2,3}	正四面形 {2,4}	正五面形 {2,5}	正六面形 {2,6}	...	{2,n}

依施莱夫利符号分类

施莱夫利符号	多面体	组成面	顶点图	孔洞	皮特里多边形
未定义	零面体	未定义	未定义	未定义	未定义
{0,0}	无边地区图[22]	零角形{0}	零角形{0}
{1,2}2	一角形二面体	一角形{1}	二角形{2}		二角形{2}
{2,1}2	一面形	二角形{2}	一角形{1}
{2,2}2	二面形（二角形二面体）		二角形{2}
{2,3}6	三面形		三角形{3}		六边形{6}
{2,n}	多面形		多边形{n}		不一定
{3,2}6	三角形二面体	三角形{3}	二角形{2}		六边形{6}
{3,3}4	正四面体		三角形{3}		四边形{4}
{3,4}3	正八面体半形 皮特里四面体的对偶多面体		正方形{4}		三角形{3}
{3,4}6	正八面体				六边形{6}
{3,5}5	二十面体半形		五边形{5}		五边形{5}
{3,5/2}10/3	皮特里大二十面体		五角星{5/2}		十角星{10/3}
{3,5}10	正二十面体		五边形{5}		十边形{10}
{3,6}	正三角形镶嵌		六边形{6}		无限边形
{3,6}4	皮特里立方体				正方形{4}
{3,10}5	皮特里十二面体的对偶多面体		十边形{10}		五边形{5}
{4,2}4	正方形二面体	正方形{4}	二角形{2}		正方形{4}
{4,3}3	立方体半形 皮特里四面体		三角形{3}		三角形{3}
{4,3}6	立方体				六边形{6}
{4,4}	正方形镶嵌		正方形{4}		无限边形
{4,5}	五阶正方形镶嵌		五边形{5}
{4,5}6	内侧菱形三十面体（抽象）[23]				六边形{6}
{4,6}	六阶正方形镶嵌		六边形{6}		无限边形
{4,6}3	皮特里八面体的对偶多面体				三角形{3}
{4,6|3}10	四角六片三角孔扭歪正三十面体			三角形{3}	十边形{10}
{4,6|4}	四角六片四角孔扭歪无限面体			正方形{4}	无限边形
{5,2}10	五边形二面体	五边形{5}	二角形{2}	未定义	十边形{10}
{5,3}5	正十二面体半形		三角形{3}		五边形{5}
{5,3}10	正十二面体				十边形{10}
{5/2,3}10/3	大星形十二面体	五角星{5/2}			十角星{10/3}
{5,4}	四阶五边形镶嵌	五边形{5}	正方形{4}		无限边形
{5,4}6	截半大十二面体（抽象）[23]				六边形{6}
{5,5/2}6	大十二面体		五角星{5/2}
{5/2,5}6	小星形十二面体	五角星{5/2}	五边形{5}
{5,6}4	双三斜十二面体（抽象）[23]	抽象五边形{5}	六边形{6}		四边形{4}
{5,10}3	皮特里二十面体的对偶多面体	五边形{5}	十边形{10}		三角形{3}
{6,2}6	六边形二面体	六边形{6}	二角形{2}		六边形{6}
{6,3}	正六边形镶嵌		三角形{3}		无限边形
{6,3}4	皮特里立方体的对偶多面体		三角形{3}		正方形{4}
{6,4}	四阶六边形镶嵌		正方形{4}		无限边形
{6,4}3	皮特里八面体		扭歪四边形{4}		三角形{3}
{6,4|4}	六角四片四角孔扭歪无限面体		正方形{4}	正方形{4}	无限边形
{6,5}	五阶六边形镶嵌		五边形{5}	未定义
{6,5}4	内侧三角六边形二十面体（抽象）[23]				四边形{4}
{6,5}5/2	皮特里小星形十二面体				五角星{5/2}
{6,5/2}5	皮特里大十二面体		五角星{5/2}		五边形{5}
{6,6|3}	六角六片三角孔扭歪无限面体		六边形{6}	三角形{3}	无限边形
{6,6}6	凹五角锥十二面体（抽象）[23]			未定义	六边形{6}
{10,2}10	十边形二面体	十边形{10}	二角形{2}		十边形{10}
{10,3}5	皮特里十二面体		三角形{3}		五边形{5}
{10/3,3}5/2	皮特里大星形十二面体	十角星{10/3}			五角星{5/2}
{10/3,5/2}3	皮特里大二十面体		五角星{5/2}		三角形{3}
{10,5}3	皮特里二十面体	十边形{10}	五边形{5}

依组成面分类

一般的凸正多面体只能由正三角形、正方形和正五边形构成；若考虑非凸的情况则可以由正五角星构成；若允许复数${\displaystyle \mathbb {C} ^{3}}$的空间，则莫比乌斯－坎特八边形也能构成正多面体。然而正七边形难以存在于平坦空间的立体中。^[24]而目前已知存有正七边形的正多面体存于双曲空间中。^[14]

二角形组成的正多面体

多面形

正二面形 {2,2} 2个二角形

正三面形 {2,3} 3个二角形

正四面形 {2,4} 4个二角形

正五面形 {2,5} 5个二角形

正六面形 {2,6} 6个二角形

...

{2,n} n个二角形

正三角形组成的正多面体

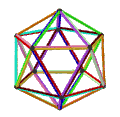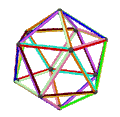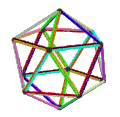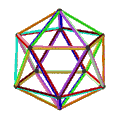
正三角形二面体 {3,2} 2个正三角形	正四面体 {3,3} 4个正三角形	八面体半形 {3,4}/2 4个正三角形	正八面体 {3,4} 8个正三角形	星形八面体 2{3,3} 8个正三角形	二十面体半形 {3,5}/2 10个正三角形	正二十面体 {3,5} 20个正三角形
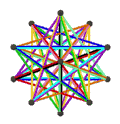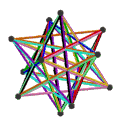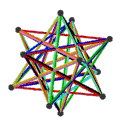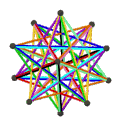
大二十面体 {3,5/2} 20个正三角形	五复合正四面体 5{3,3} 20个正三角形	十复合正四面体 10{3,3} 40个正三角形	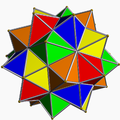五复合正八面体 5{3,4} 40个正三角形	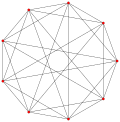2{3}2{4}p p3个正三角形	正三角形镶嵌 {3,n} 无穷个正三角形

正方形组成的正多面体

正方形二面体 {4,2} 2个正方形

立方体半形 {4,3}/2 3个正方形

立方体 {4,3} 6个正方形

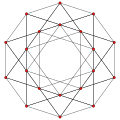扭歪正三十面体 {4,6|3} 30个正方形

五复合立方体 5{4,3} 30个正方形

扭歪288面体 {4,8|3} 288个正方形

扭歪p2面体 {4,4|p} p2个正方形

多立方体 {4,6|4} 无穷个正方形

正方形镶嵌 {4,n} 无穷个正方形

五边形组成的正多面体

形状	正五边形二面体 {5,2}	十二面体半形 {5,3}/2	正十二面体 {5,4}	大十二面体 {5,5/2}	大星形十二面体 {5/2,3}
面的组成	2个正五边形	6个正五边形	12个正五边形	12个正五边形	12个正五角星形
形状	小星形十二面体 {5/2,5}	抽象正二十四面体[23] {5,4}6	抽象正二十四面体 {5,6}4	五边形镶嵌 {5,n}
面的组成	12个正五角星形	24个抽象正五边形 具像化由： 12个正五边形和 12个正五角星形	24个抽象正五边形 具像化由： 12个正五边形和 12个正五角星形	无穷个正五边形

六边形组成的正多面体

六边形二面体 {6,2} 2个正六边形

扭歪二十面体 {6,4|3} 20个正六边形

多八面体 {6,4|4} 无穷个正六边形

多四面体 {6,6|3} 无穷个正六边形

正六边形镶嵌 {6,n} 无穷个正六边形

七边形组成的正多面体

双曲正七边形镶嵌。

参见：§ 正七边形组成的双曲无限面体

在实数空间的欧几里得空间（平坦空间）中，正七边形无法构成正多面体^[25]。由正七边形组成的正多面体（如三阶七边形镶嵌蜂巢体中的正七边形镶嵌形状的胞）只能存于双曲空间中^[14]。

八边形组成的正多面体

参见：§ 正八边形组成的双曲无限面体

在实数空间的欧几里得空间（平坦空间）中，正八边形无法构成正多面体，更精确地说，即多边形边数超过5的正多边形（如正六边形、正七边形、正八边形等）皆无法组成正多面体，这个观点在欧几里得的《几何原本》中给出了证明^[4]（参见帕雷托立体 § 几何证明）。因此由正八边形组成的正多面体只能存于其他空间中，如双曲空间中正八边形镶嵌形状的胞、部分视为球面多面体的球面镶嵌（如正八边形二面体）以及复空间中的一种由8条三元边和8个顶点构成的多边形（莫比乌斯－坎特八边形^[26]）可以构成2种复空间正多面体。^[27][28]

形状	正八边形二面体 {8,2}	黑塞二十七面体 3{3}3{3}3	截半黑塞二十七面体 3{3}3{4}2	八边形镶嵌 {8,n}
面的组成	2个正八边形	27个正莫比乌斯－坎特八边形	54个正莫比乌斯－坎特八边形	无穷个正八边形

相关多面体

帕雷托立体可以透过康威变换变换成13种阿基米德立体^[29]，其他正多面体也可以透过康威变换变换成半正多面体或均匀多面体：

原像	康威变换
	截角	截半	截棱	过截角	对偶	对偶复合	小斜方截半	大斜方截半	扭棱	加锥	会合
正四面体	t0,1{3,3}	t1{3,3}	c{3,3}	t1,2{3,3}	t2{3,3}	2{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}	三角化	三角化会合
立方体	t0,1{4,3}	t1{4,3}	c{4,3}	t1,2{4,3}	t2{4,3}	{4,3}{3,4}	t0,2{4,3}	t0,1,2{4,3}	sr{4,3}	四角化	四角化会合
正八面体	t0,1{3,4}	t1{3,4}	c{3,4}	t1,2{3,4}	t2{3,4}	{3,4}{4,3}	t0,2{3,4}	t0,1,2{3,4}	sr{4,3}	三角化	三角化会合
正十二面体	t0,1{5,3}	t1{5,3}	c{5,3}	t1,2{5,3}	t2{5,3}	{5,3}{3,5}	t0,2{5,3}	t0,1,2{5,3}	sr{5,3}	五角化	五角化会合
正二十面体	t0,1{3,5}	t1{3,5}	c{3,5}	t1,2{3,5}	t2{3,5}	{3,5}{5,3}	t0,2{5,3}	t0,1,2{5,3}	sr{5,3}	三角化	三角化会合
大十二面体	t0,1{5,5/2}	t1{5,5/2}	c{5,5/2}	t1,2{5,5/2}	t2{5,5/2}	{5,5/2}{5/2,5}	t0,2{5,5/2}	t0,1,2{5,5/2}	sr{5/2,5}		五角化会合
小星形十二面体	t0,1{5/2,5}	t1{5/2,5}	c{5/2,5}	t1,2{5/2,5}	t2{5/2,5}	{5/2,5}{5,5/2}	t0,2{5/2,5}	t0,1,2{5/2,5}	sr{5/2,5}	五角化	五角化会合
大二十面体	t0,1{3,5/2}	t1{3,5/2}	c{3,5/2}	t1,2{3,5/2}	t2{3,5/2}	{3,5/2}{5/2,3}	t0,2{3,5/2}	t0,1,2{3,5/2}	sr{5/2,3}		五角化会合
大星形十二面体	t0,1{5/2,3}	t1{5/2,3}	c{5/2,3}	t1,2{5/2,3}	t2{5/2,3}	{5/2,3}{3,5/2}	t0,2{5/2,3}	t0,1,2{5/2,3}	sr{5/2,3}	五角化	五角化会合
星形八面体	t0,1(2{3,3})			t1,2(2{3,3})	t2(2{3,3})
黑塞二十七面体		t1(3{3}3{3}3)			t2(3{3}3{3}3)

备注：粗体或灰底表示变换完的结果仍为正多面体者。

参见

• 正图形列表
• 正多面体